Insights-ヒント集


Please Wait
Insights:豆知識やヒントの共有
正しい情報を得られれば、何時間もの作業を軽減することができます。しかしそのような貴重な知識の多くは、教科書には載ってなく、授業で教えられているものでもありません。またオンラインソースを検索しても簡単に見つけられるものでもありません。このような知識の多くは経験から得られることが多く、フォトニクスの世界で働く人々の頭の中やラボノートの中にとどめられています。
当社ではこのような経験から得られたヒントや豆知識、ガイドライン、実践的なテクニックを集め、Insightsというヒント集にまとめました。現段階で集めたヒント集は下記のリンクや上のタブからご覧いただけます。こちらのページは随時更新して内容を拡充してまいります。
フォトニクスの世界
- フォトニクスとは?
光学部品のアライメント
- レーザのポインティング角度を補正する手順
- 2つのミラーを使用して別の経路に沿うようにレーザ光をアライメントする方法
- 2つのビームステアリングミラー間に必要な距離
ビームエキスパンダ
- 自作のケプラー式ビームリデューサの例
- レーザービーム径を拡大することで効果的にビーム発散角を縮小できるか?
- ビームエキスパンダまたはレデューサの方式(ケプラー式、ガリレイ式)とその特徴
光学実験のベストプラクティス
- テーブルクランプ:保持力を最大にする方法
- 光学テーブル:テーブルクランプとテーブル面の歪みについて
- ワッシャ:オプトメカニクスへの使用方法
- 電気信号: AC結合 vs DC結合
- ファイバーコリメータ:アダプタを使った取付け方法
- 移動ステージ中央の大きな取付け穴の使い方
- 直線ステージ取付けスロットの使い方
- 低パワー光の測定方法を改善する最初のステップ
コリメーション
- コリメート光は無限遠まで一定のビーム径を維持するか?
- コリメート用レンズから出射された光のビームスポットは、ランプやLEDなどの光源の像か?
当社製品の設計要素
- 移動ステージに取付けられたコンポーネントを、アジャスタを介して伝わる振動から絶縁できるか?
- ポストホルダ:穴の内側の長方形の溝について
- ベースは、アンダーカットのある面を下向きに置くと安定します
光ファイバ
- NAはファイバの受光角を表す指標となり得るか?
- MFDがシングルモードファイバにおいて重要な結合パラメータである理由とは?
- NAによりシングルモードファイバからのビーム広がり角がわかるか?
- シングルモードファイバへの光の結合効率に影響する因子は?
- 最大受光角はマルチモードファイバのコア全体に渡り一定か?
イメージング
- コンデンサの開口数(NA)は顕微鏡の分解能に影響を与えるか?
- 顕微鏡におけるケーラー照明について
積分球
- 積分球から放射されるUV蛍光および青色蛍光
- 試料交換誤差について
レーザ
- レーザ装置からは、いつでもその筐体の軸に平行なコリメート光が放射されるか?
- 量子カスケードレーザ(QCL)とインターバンドカスケードレーザ(ICL):動作限界と発熱によるロールオーバ
- HeNeレーザ:取扱い方と取付け方のガイドライン
- チョッパーホイールを使用したビームサイズの測定法
- レーザ光に薄レンズの公式を適用できるか?
レンズマウント
- C-マウントとCSマウントのカメラとレンズに互換性はあるか?
- 当社のサイエンティフィックカメラにアダプタは必要か
- フランジバックがカメラのフランジとセンサ間の距離よりも短くなる場合がある理由は?
モーションコントロール
- 手動ステージを電動ステージに変える方法
- デジタルマイクロメータからの位置情報の記録
軸外放物面(OAP)ミラー
- なぜ球面ミラーではなく放物面ミラーを使うのか?
- 軸外放物面(OPA)ミラーの利点
- OAPミラーの軸外し角
- OAPミラーを使用したコリメート光の集光、および点光源からの光のコリメート
- OAPミラーの光軸と集光軸の特定方法
- OAPミラーをペアで使用すると像のリレーやビームへのアクセスが可能になります
- OAPミラーの取付けとアライメント
- OAPミラーをベースにした反射型コリメータにおける光の方向性
光アイソレータとファラデー効果
- ファラデー効果の大きさを測定する方法
- ファラデー回転の方向と回転角の大きさを求めるには何が必要か?
フォトダイオード
- 立ち上がり時間の波長依存性について
偏波保持(PM)ファイバ
- 偏波保持ファイバはすべての入射光の偏光状態を維持するか?
- 偏波保持ファイバはどのようにして直線偏光を維持するのか?
- PANDA型およびボウタイ型偏波保持ファイバからの出射光の消光比(ER)を制限する要因
- ビート長とは?ビート長が偏波消光比の代わりに偏波保持ファイバの仕様として明記されている理由
- ストレスロッド(応力付与ロッド)タイプの偏波保持ファイバの温度依存性
偏光
- 垂直成分と平行成分の識別に使用されるラベルについて
- 偏光偏光楕円と偏光状態の関係
- 偏光状態を表すのにポアンカレ球が役に立つ理由
- 非偏光の光源を使用して偏光素子の消光比を測定する方法
- 直線偏光の光源を使用して偏光素子の消光比を測定する方法
リフレクタ
- レーザのビーム径に基づいてミラー径を選択するルールはあるか?
- ビームのアライメントはレトロリフレクタで反射されるビーム光路にどのように影響するか?
- レトロリフレクタープリズムの裏面を金属コーティングする理由は?
- コーナーキューブへの入射角は出射ビームのパワーに影響を及ぼすか?
デバイス制御のためのソフトウェアと書込みプログラム
- デジタルマイクロメータDM713: LabVIEWおよびC#プログラミングリファレンス
Video Insights (How-to動画集)
- レーザのアライメント方法
- 精度を高めるための光パワーメーターパラメータの設定方法
- 手動ステージを電動ステージに変える方法
- ポストホルダを光学テーブル、ベース、ブレッドボードなどにボルトで固定するときの注意点
- 光アイソレータの調整方法
- 直線偏光子の軸をテーブルに対して垂直または平行にアライメントする方法
- ハンドヘルド型スクライブを使用して大きな直径の石英ファイバをクリーブする方法
- 光ファイバ用コンポーネントの挿入損失測定
- 1/4波長板(QWP)を使用して円偏光に変換する方法
- 直線偏光子を入射面に対して45°にアライメントする方法
- 2本のシングルモードファイバ間にコリメートされた自由空間光を生成するためのファイバーコリメータのアライメント方法
- TO-Can型半導体レーザのセットアップ方法(Viewer Inspired)
- ピグテール付きバタフライパッケージ型半導体レーザのセットアップ方法(Viewer Inspired)
- 1/4波長板のファスト軸とスロー軸を区別する方法
- Visual Studio®プロジェクト作成とC#プログラミング: Kinesis® BBD300シリーズコントローラを使用して
- 偏光計を構築して、ストークス値と偏光状態を特定する方法(Viewer Inspired)
- Visual Studio®とC#プログラミングによるラスタスキャン:Kinesis® BBD300シリーズコントローラを使用して
- 軸外放物面(OAP)ミラーをアライメントしてビームをコリメートする方法(Viewer Inspired)
- Visual Studio®とC#プログラミングによるカメラのセットアップと画像取得
- FiberBench上でのFiberPortのアライメント方法(Viewer Inspired)
- KF(QR)真空フランジの使い方
- ベース、ポストホルダ、ポストなどを取り付ける際の注意点
- レーザースペックルを利用してビームの焦点を見つける方法
- Python®によるパワーメータと回転マウントの自動化(Viewer Inspired)
- 真空対応CF(コンフラット)フランジの使い方
- 空間光変調器(SLM)の位相遅延の校正方法
- シヤリングプレートコリメーションテスタを用いてレーザ光をコリメートする方法(Viewer Inspired)
- 偏波保持ファイバに結合する入射光の偏光方向をアライメントする方法(Viewer Inspired)
- ヘリオットセルのセットアップと構成(Viewer Inspired)
- LEDからの出力光をコリメートする方法
- 追尾機能を備えた太陽撮像望遠鏡の構築
- 光の透過率とブリュースター角の入射角依存性
フォトニクスとは
フォトニクス(光工学)とは光の応用や研究です。フォトニクスの語源は「光子(photon)」、つまり光の粒子です。これは荷電粒子である電子が電流を構成するエレクトロニクス(電子工学)に似ています。 フォトニクスにおいては、光子は光を構成するエネルギー粒子です。光子がもたらすエネルギーの量は色(波長)に依存します。例えば、赤色(640 nm)の光を1 mW出力するレーザーポインタは、 光は様々な光源によって生成されます。太陽、炎、生物発光(蛍)など自然に生成される光があります。人工的に生成される光には電球、LED、レーザからの光があります。 電流を運ぶ電線と同じように、光は光ファイバで1つの場所からほかの場所に運ばれます。 | エレクトロニクスでは抵抗器やコンデンサを使用して回路を通る電流を調整しますが、フォトニクスではレンズやミラー、プリズムなどの光学素子を用いて光を誘導し、光路を調整します。 光の解析は、エレクトロニクスとほぼすべて同じ測定器を使用しますが、最初に光子を電流に変換する必要があります。 フォトニクスは一般的に距離の測定(レーザーレーダ)、情報の送受信(通信)、目視できない物体のイメージング(顕微鏡、内視鏡、ボアスコープ)、そして、血液内の酸素量(パルスオキシメータ)や粒子検出器、ガス検出器などのセンサ内で用いられます。 |
最終更新日:2022年4月20日
1
レーザのポインティング角度を補正する手順
キネマティックマウントのピッチ(チップ)とヨー(ティルト)を調整することで、レーザ角度の微細な補正を行うことができます。この角度調整は、コリメートされたレーザ光を光学テーブル表面に水平、あるいはテーブルのタップ穴のラインに沿ってなど特定の方向にアライメントする際に行なわれます。
Click to Enlarge
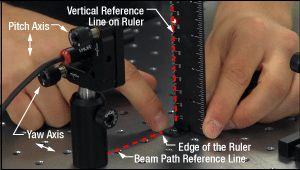
図2:ビームは、光学テーブルのタップ穴のラインに対して平行になるようアライメントすることができます。キネマティックマウントのヨー調整でビーム角度を調整し、ルーラをタップ穴のラインに沿ってスライドさせるときに、ビームがルーラの縦の基準線上に保持されるようにします。

Click to Enlarge
図1:ビーム方向を光学テーブルの表面に対して水平にするには、レーザ用キネマティックマウントのピッチ調整を使用します(図2)。ビームがテーブル表面に対して平行になっている状態は、ビーム高がレーザ前面に近い位置(左)と遠い位置(右)でパワー測定値が同じであることを確認することで行います。
動画3:コリメートレーザーパッケージPL202からのビームのポインティング角度は、レーザのキネマティックマウントKM100のピッチ(チップ)とヨー(ティルト)アジャスタと、ルーラBHM1の水平と垂直線を使用して補正しました。その結果、ビームは光学テーブルの表面に対して平行かつタップ穴のラインに沿って伝搬します。
マウントのアジャスタを使用する前に
まず、キネマティックマウントの各アジャスタを回して移動範囲の中央に移動させます。これにより調整範囲が足りなくなるリスクが少なくなります。また調整範囲の真ん中にアジャスタがあると、マウントのポインティング安定性が良くなります。
その後、レーザを支えるポストやポストホルダなどのオプトメカニクス部品を調整することで、レーザの高さ、位置、向きの粗調整を行います。 調整後はすべての固定ネジが締め付けられていることを確認してください。
ビームをテーブル表面に対して平行にする場合
レーザ光のレベル調整のため、アライメントツールを用いて、マウントのピッチアジャスタによる微細な調整を繰り返す必要があります。
まず光源から近い位置と遠い位置のビームの高さを測定します(図1)。2つの間の距離が長ければ長いほど、確度は高くなります。 2つの位置のビーム高が一致するまで、キネマティックマウントのピッチを繰り返し調整します。
調整を繰り返すと、ビーム高さも変わってくる可能性があります。動画3の例では、光源に近いビーム高は当初82 mmでしたが、最初のピッチ調整で83 mmに上がっています。
調整後のビーム高さを変えたいときは、水平調整を行なった後、レーザを支えるオプトメカニクス部品により高さ調整を行います。レーザ高さを調整する方法として、2つのステアリングミラーをレーザの後ろに置き、アライメントする方法もあります。ステアリングミラーは特に設置型レーザを使用し、ビーム出力方向を調整する際に有用です。
ビームをタップ穴列に沿った向きにする
ビームをテーブルのタップ穴列に対して平行にアライメントすることもまたアライメントツールとマウントのヨーアジャスタの調整が必要な反復プロセスにより行います。
タップ穴列を基準線としたレーザ出力方向を調整するためには、アライメントツールが必要になります。ルーラのベース部の端をタップ穴列の端に合わせて配置します(図2)。
テーブル上の基準線に対するビームの角度ズレは、ルーラに照射されるレーザースポット位置とルーラの垂直基準線の差を見ることで確認できます。垂直基準線として、ルーラ端や目盛端を利用できますが、それでは不十分な場合には、取付けブラケットBHMA1を使用して水平置き型のルーラを取り付けることができます。
動画3では、ルーラをタップ穴列に並行に移動し、レーザ照射位置をルーラーの1 mm単位の目盛の端に一致させるようにアライメントします。ルーラを基準線の遠い方の位置に移動させると、ルーラのビーム位置も水平方向に移動します。ルーラを遠い方の位置に配置した後、ビーム端が1 mm単位の目盛端に一致するまでマウントのヨーを調整します。その後ルーラを光源の近くに移動させ、ビームの位置調整の結果を見ます。このプロセスは必要に応じて反復で行われています。
ビームアライメントに関する追加情報はこちらの動画ページでご覧ください。
最終更新日:2020年10月12日
2つのミラーを使用して別の経路に沿うようにレーザ光をアライメントする方法
1つ目のステアリングミラーは、新しい光路上に配置された2つ目のミラーに向けてビームを反射します。2つ目のステアリングミラーは、新しい光路に沿うようにアライメントします。2つのステアリングミラーでレーザ光をアライメントする手順は、Walking the Beam(ビームの移動)として説明することがあり、その結果はFolded Beam Path(折りたたまれたビーム路)と呼ばれることがあります。動画4の例では、ビームを新しい光路にアライメントするために2つのアイリスが使用されています。新しい光路は光学テーブル面に対して平行で、タップ穴列に沿っています。
Click to Enlarge
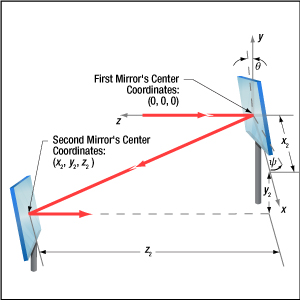
図3:1つ目のミラーから反射されたビームは、x軸ならびにy軸まわりに、それぞれ θおよびψ回転すれば、2つ目のミラーに入射します。どちらの角度も2つ目のミラーの中心位置(座標x2 , y2 , z2 )に影響を及ぼします。1つ目のミラーのx軸周りの回転は、マウントのピッチ(チップ)アクチュエータの移動範囲によって制限されますが、その移動範囲は、2つ目のミラーの位置と高さも制限します。

Click to Enlarge
図 5:2つ目のキネマティックミラーマウントのアジャスタは、2つ目のアイリスにビームをアライメントするのに使用します。

Click to Enlarge
図4:1つ目のキネマティックミラーマウントのアジャスタを調整して、1つ目のアイリスの開口部にレーザースポットを合わせています。
動画4:キネマティックマウントKM100の2つのミラーが、コリメートレーザーパッケージPL202からの光を2つのアイリスIDA25によって規定された光路に誘導します。観察用のスクリーンとして2つ目のアイリスの後ろに置かれたルーラBHM1上にビームスポットが現れ、また、2つのアイリスの開口部周辺にボヤっ光が当たっている 状態みなればビームがアライメントされている状態とみなせます。
ミラーの高さの設定
1つ目のミラーの中心は、入射路の高さと一致させます。2つ目のミラーの中心は、新しい光路の高さに合わせてください。
アイリスのセットアップ
新しい光路はアイリスによって設定されます。動画4では光路がテーブル面に対して水平となるよう、アイリスの高さが一致していることがご覧いただけます。マウント内のアイリスの高さはルーラかノギスを使用すると適度な精度で設定可能です。
アイリスが閉じているときの(小さな)開口部は、完全な中心位置にない場合があります。そのため、ビームに面するアイリスの左右を交換すると、開口の位置がシフトする場合があります。ビームに面するアイリスの面を決めたらセットアップから使用まで同じ面を使用することを推奨します。
コンポーネントの配置と粗調整
まず、両ミラーのアジャスタを回しながら移動範囲の中央に移動させます。1つ目のミラーは入射光路に配置し、2つ目のミラーは新しい光路内での位置を決めます(図3)。1つ目のミラーのピッチ(チップ)アクチュエータの移動範囲がx周りのミラーの回転(θ )を制限するため、ミラー配置は1つ目のミラーのピッチ(チップ)アクチュエータの移動範囲によって制限されます。2つ目のミラーの位置
新しい光路に2つ目のミラーを配置後、両方のアイリスを光路上に置いてください。1つ目のアイリスは2つ目のミラーの近くに、2つ目のアイリスは2つ目のミラーからできるだけ遠くに配置してください。
2つのミラーの高さはそのまま維持し、またヨーのアジャスタは触らずに1つ目のミラーを回転させて、光を2つ目のミラーに向けます。1つ目のミラーのピッチアジャスタを調整して、レーザースポットを2つ目のミラーの中心近くに移動させます。その後、2つ目のミラーを回転させて、ビームを新しい光路にある程度向けます。
最初に光路上に光を当て、その後、向きを調整します。
1つ目のミラーは、2つ目のミラー上にある新しい光路上の点に向けてビームをステアリングするために使用します。まず、1つ目のアイリスのレーザースポットの位置を見ながら1つ目のミラーのアジャスタを調整します(図4)。アイリスの開口部の中心にレーザースポットが合えば最初のステップは終了です。
次に2つ目のミラーでビームをステアリングして、新しい光路とアライメントさせます。2つ目のミラーのアジャスタを調整して、レーザースポットを2つ目のアイリスの開口部に移動します(図5)。ピッチアジャスタがビームの高さを調整し、ヨーアジャスタがビームを横方向に移動します。2つ目のアイリスでレーザースポットが消えてしまう場合、2つ目のミラーのレーザースポットが新しい光路から離れています。
1つ目のミラーのアジャスタを調整しながら2つ目のミラー上のビーム位置を変え、1つ目のアイリスの開口部の中心にレーザースポットがあたるようにします。2つ目のミラーのアジャスタ調整を再開して、2つ目のアイリスの開口部にレーザースポットを向けます。これをレーザービームが両方のアイリスの中心を通るまで繰り返します(動画4)。アジャスタのどれかが調整範囲の制限に近づいてしまったら、ミラーの1つ、あるいは両方の位置を変え、アライメント手順を繰り返してください。
ヨー軸のアジャスタが制限に近づいた場合、反射ビーム方向を記録しておき、ヨーアジャスタを調整範囲の中央に回転させます。反射ビーム方向が記録した位置になるようミラーマウントの向きを変えます。ミラーが回転できない場合、ビームが新しい光路にほぼ沿うよう1つあるいは両方のミラーの位置を変えます。ビームの向きが微細に調整できるまでこのアライメント手順を繰り返します。
ピッチ軸のアジャスタが制限に近づいた場合、2つのミラーの間の距離を長くするか、入射路あるいは新しい光路の高さの差を小さくします。どちらの方法でもアライメント手順が繰り返された後、ピッチアジャスタが調整範囲の中心の近くに配置されます。
ビームアライメントに関する追加情報はこちらの動画ページでご覧ください。
最終更新日:2020年10月22日
2つのビームステアリングミラー間に必要な距離
2つのステアリングミラーの間に必要な距離(図6)は、1つ目のミラーから反射するビームの傾斜と、2つのミラーの高さの差によって決まります。必要な距離を把握することは、ブレッドボードや光学テーブル上のセットアップのスペースを見積もるのに重要です。
入射ビームに対する1つ目のミラーのピッチ(tip)だけを使用した簡単な計算をしがちですが、ヨー(tilt)を無視してしまうと、ミラー間の必要な距離がかなり低く見積もられる場合があります。下の例では、マウント全体ポスト軸を中心に回転することでヨー調整を行い、マウントのアジャスタでピッチ調整を行うという仮定で距離が計算されています(図7)。この手法はしばしばミラーを初期配置するときに使用されます。
Click to Enlarge
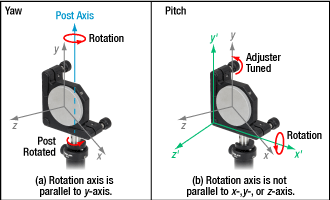
図 7:ヨーアジャスタを使用する代わりに、ポスト軸中心にマウント全体を回転させることで、初期のミラー調整(ヨー)を行います(左図)。これによりマウントがX、Y、Z軸と入射光に対して回転します。マウントのピッチアジャスタがミラーのピッチを調整し(右)、マウントのX、Y、Z軸に対してミラーの向きを変えます。上の写真はミラーマウントKS2と位置保持用ポストカラーRMCです。
Click to Enlarge
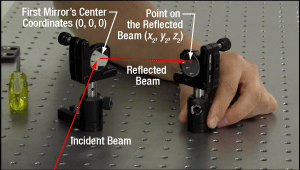
図 6:1つ目のミラーが入射ビームを反射して2つ目のミラーに送ります。2つのミラー間に必要な距離は、1つ目のミラーのピッチとヨーの両方に依存します。これらのミラーマウントKM100は±4°の範囲に渡りピッチとヨーの調整が可能です。
Click to Enlarge
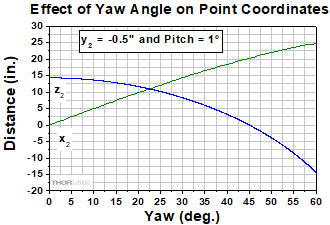
図9:これらの値は、図8で説明するセットアップを使用して計算されています。ただし1つ目のミラーのピッチ角は1°と仮定しています。この結果では、ピッチを小さくすると、2つのミラーの間に必要な距離が長くなることを示しています。しかし、アジャスタが調整範囲の制限いっぱいまで使用すると安定性が悪くなることを考慮すると、距離をある程度長くすることを許容しても良さそうです。
Click to Enlarge
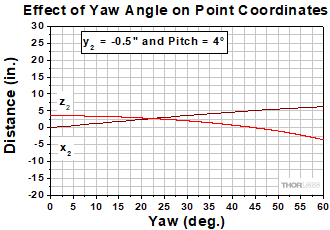
図8:この例では2つ目のミラーのテーブル上の配置に関して、入射ビームより12.7 mm低い(y2 = -0.5")位置にあるときでもに反射ビームが受光できる位置を決めるのが目標です。1つ目のミラーのピッチはアジャスタの最大調整範囲である4°と仮定しています。マウント全体をポスト軸中心に回転させ、1つ目のミラーのヨーを変えます。マウントのヨーアジャスタを使用しないのは、ヨー角度は4°以上必要で、かつこのステップではミラーの向きの微調整が必要ないからです。
Click to Enlarge
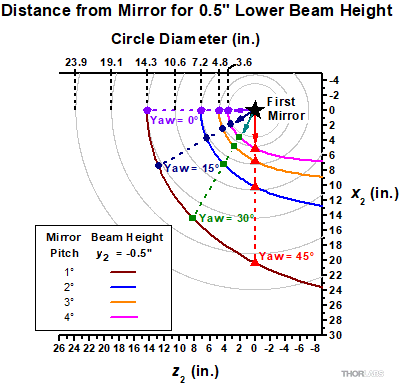
図10:このグラフはテーブル面を上から見た位置を示しています。1つ目のミラー(星印)が始点です。枠内で定義されている曲線は2つ目のミラーの位置のいくつかの例を示しており、2つ目のミラーは1つ目のミラーよりも12.7 mm低い高さ(y2)でビームを受光します。ミラー間の距離は、ピッチ角が一定でも1つ目のミラーのヨー角によって大幅に長くなります。
ヨーとピッチを適用する
ビームステアリングミラーの配置は、一般的に2つのステップで行います。まずミラーを大まかな位置と向きで置いてから、向きの微調整を行います。
ここの例ではまず調整の最初ステップを行い、その後のピッチとヨーの調整は異なる方法を用いることを想定しています。必要なヨー角度がマウントのアジャスタのヨーの調整範囲よりも大きいことが多いため、ポスト軸中心にマウント全体を回転させることでヨー調整を行います(図7、左)。これでマウントに対する入射ビームの角度が変わります。ヨーアジャスタは使用せず、マウントのピッチアジャスタだけ使用します。ピッチアジャスタは、入射ビームとマウントにおけるすべての軸の両方に対して、ミラーの向きを変えます(図7、右)。
ミラーの向きは通常、ポスト軸中心にマウントを回転させることなく、マウントのピッチとヨーのアジャスタを使用して微調整をします。両方のアジャスタを使用することは、ここでご紹介している方法例とは異なる効果でミラーの向きを変えます。
反射ビーム上の点の座標
1つ目のミラーの中心は、デカルト座標系の始点として選択されています(図7)。 Z軸は、入射光とは平行です。Y軸はテーブル面に対して垂直方向です。
ポストとX軸周りの回転角度(それぞれ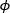 とθが既知である場合、反射ビームに沿っている点
とθが既知である場合、反射ビームに沿っている点
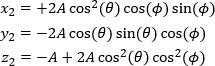
変数Aはスケールファクタです。大きければ大きいほど点とミラーの間の距離は長くなります。この例では、既知の高さの変化(y2 )をx2およびz2 の算出に使っています。
例:ステアリングミラーのセットアップ
これらの式は、ビームの高さや方向を変えるステアリングミラー2つを配置するのに役立ちます。1つ目のミラーの中心は入射ビームの高さ、2つ目のミラーの中心は新しい光路の高さに設定します。2つ目のミラーは、新しい光路の高さで反射ビームを受光する必要があります。
この例では、どちらの光路も光学テーブルに対して平行ですが、新しい光路は入射路よりも12.7 mm低くなっています。ミラーはキネマティックマウントKM100に固定されており、マウントはポストホルダで固定したポストの上に取り付けられています(図6)。マウントのピッチとヨーのアジャスタはそれぞれ調整範囲に±4°の制限があります。この範囲は最初にミラーのピッチを設定するには十分ですが、ミラーのヨーには十分ではありません。代わりに入射ビームとミラー間のヨーは、ポスト軸中心にマウント全体を回転させることで調整します。これによりヨーの調整範囲の制限がなくなります。
図8では、2つ目のミラーのx2 とz2 座標が、1つ目のミラーのヨー角に対してプロットされています。これらの値は、新しい光路の任意の高さ
図10では、2つ目のミラーのx2とz2 の座標を光学テーブルの位置としてプロットしています。テーブルを上からみたときの位置です。1つ目のミラーの位置は星印、グレーの円は星印中心の同心円です。矢印は反射光の方向で、いずれも異なるヨー角度に相当します。枠内で定義されている曲線は異なるいくつかのピッチ角と、ビーム高の差-12.7 mmに対して算出されています。曲線をグレーの円と比較すると、ヨー角が大きくなると2つのミラーの間の距離を長くする必要があることが示されています。ピッチ角が小さくなっても距離を長くする必要があります。
ビームアライメントに関する追加情報はこちらの動画ページでご覧ください。
最終更新日:2021年1月5日
自作のケプラー式ビームレデューサの例
ビームレデューサは、低パワーの連続発振(CW)レーザとフリースペース型アイソレータとの間に設置するために設計しました。レーザの波長はアイソレータの動作範囲内でしたが、ビーム径はアイソレータの最大仕様を超えていました。ビームレデューサはケプラー式望遠鏡をベースにして設計し、2つの正レンズを用いて組み立てました。

Click to Enlarge
図1: ケプラー式ビームレデューサは、レーザ光のビーム径を縮小するように製作されており、光アイソレータの入射口および出射口でビーム径がクリッピングされることなく通過する必要があります。

Click to Enlarge
図2:ビームレデューサでは、正の焦点距離を有する2枚のレンズが、各レンズの焦点距離の和に等しい距離で配置されています。縮小率は、出射側レンズの焦点距離を入射側レンズの焦点距離で除した値に等しくなります。ビームレデューサの構成部品については上の写真をご覧ください。出射ビームの径は、レンズチューブSM1V10の長さを変えながらビーム径を計測することで、適切に調整することができます。
ビーム径の要件
レーザ光源PL201は、波長520 nm、光パワー0.9 mW(典型値)のコリメートされた連続光を出力します。レーザから5 cm離れた距離では、直径3 mmの円内にビームパワーの99%以上が含まれます。
しかし、フリースペース型アイソレータ
縮小率とレンズの選択
ビームレデューサは、多くの場合は2枚のレンズを用いたケプラー式またはガリレイ式望遠鏡をベースに設計されます。どちらの方式もこの用途に対しては同様の性能を発揮しますが、ケプラー式の設計では光線追跡のジオメトリを利用してレンズの配置を描画し、さらに出射光のビーム径を表示することが容易なため、ケプラー式による設計を選択しました(図2下)。
ここでは、正の焦点距離を有する、反射防止コーティング付きのØ25.4 mm平凸レンズを選択しました。ビーム径よりも大きな有効径のレンズを選択し、レンズの曲面側をコリメート光側に向け、平面側をビームの焦点側に向けて設置することで、収差を小さく抑えることができます(図2下)。また、Ø25.4 mm(Ø1インチ)光学素子は、Ø25 mm~Ø25.4 mm(Ø1インチ)レンズチューブおよび関連アクセサリに直接取り付けることができます。
縮小率(m )は、目的の出射ビーム径を入射ビーム径で除することで得られます
ビームの縮小が広がり角に与える影響
ビームレデューサはビームウェスト径を縮小させますが、そのために広がり角を増加させます。ビームレデューサの出射面近傍でのビーム径は2.1 mmになりますが、ビームが伝搬するに従って回折効果によってビーム径は拡大します。このアプリケーションでは、ビームがクリッピングされずにアイソレータに入るには、約18 cmの自由空間を伝搬した後でのビーム径が2.7 mm未満でなければなりません。
縮小されたビームがアイソレータの入射径の仕様を満たし、クリッピングされずにアイソレータを通過できるかを確認するには、まず次のようにレーザ光のビームウェスト径
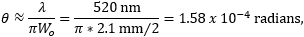
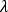 はレーザ光の波長です
はレーザ光の波長です

が得られます。次に、この式における距離を大きくして
具体的な構成
理想的なビームレデューサの設計(図2下)では、入射光のビームウェストは、左側のレンズの入射側曲面からその焦点距離(50 mm)だけ離れていると仮定します。その条件下では、光は図のようにレンズの出射側平面から焦点距離だけ分離れた場所で焦点を結びます。この入射条件が満たされない場合は、最初のレンズから出射されるビームは正確に50 mm離れた位置で焦点を結ぶことはなく、またビームレデューサから出射したビームの径は理想的な計算値にはなりません。ビームレデューサから必要な距離にわたって仕様を満たすビーム径を得るには、2枚のレンズ間の距離を理想的な設計値から調整する必要がある場合があります。このアプリケーションでは、この間隔が調整できるように筐体を構成しています。
2枚のレンズの位置を約85 mm離して固定している筐体は、レンズチューブで構成されています(図2)。この図のように、レンズの曲面はコリメート光の方向を向いています。長さ76.2 mm(3インチ)のチューブ部分(固定長)は、長さ25.4 mm(1インチ)のレンズチューブSM1L10と長さ50.8 mm(2インチ)のレンズチューブSM1M20を用いて組み立てています。焦点距離35 mmのレンズはØ25 mm~Ø25.4 mm(Ø1インチ)レンズチューブ内に固定されています。焦点距離50 mmのレンズを保持している調整機能付きレンズチューブSM1V10は、不足している長さを追加し、さらに2枚のレンズ間の距離を最適化する機能を果たします。このアセンブリは、アイソレータのアライメント中はレンズチューブマウントSM1RCで保持されています。
このビームレデューサの使用方法はこちらの動画ページでご覧ください。
最終更新日: 2021年6月18日
レーザービーム径を拡大することで効果的にビーム発散角を縮小できるか?
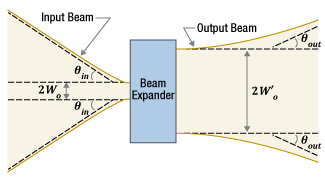
ビームエキスパンダは、ウェストが小さく発散の大きな入射光をウェストが大きく発散の小さな光に変換します。そのため、ビームエキスパンダから離れた位置における出射光のビーム径を、入射光がそのまま伝搬したときのビーム径に比べて小さくすることができます。回折効果により、ビーム径は距離によって変化します。ウェストの小さなビームのビーム広がり角は大きいため、ビームエキスパンダを使用してウェスト径を大きくすることで、ビームがウェスト部分から離れるにつれてビーム径が大きくなる割合を小さくすることができます。ビームエキスパンダは、ビームの広がり角を小さくして、出射光のウェスト位置から離れた位置でのビーム径が特定の値を超えないようにするためによく使用されます。
Click to Enlarge
図 3:入射光のウェスト径は出射光のウェスト径よりも小さいです。しかし、ウェスト径の小さな入射光の伝搬に伴うビーム径の変化は、ウェスト径の大きな出射光の変化に比べて十分に大きいです。上図のような限られた領域内でも、入射光の径は出射光の径よりも大きくなります。
Click to Enlarge
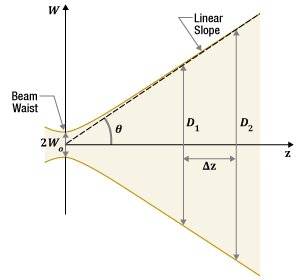
図4: ビームウェストから遠く離れると、ビームの広がり角はほぼ一定になります。本文で説明されているように、この角度
ビームエキスパンダ(およびレデューサ)
ビームエキスパンダ(およびレデューサ)に、あるウェスト径のコリメート光を入射すると、異なるウェスト径のコリメート光を出射します。拡大率あるいは倍率(m)は、
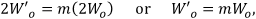
で与えられ、これはビームエキスパンダの前後のビームウェスト径
入射光および出射光のウェスト位置におけるビームの断面を測定することで、ウェスト径を推定できます。出射ビームのウェスト位置は、多くの場合はメーカによって特定されていますが、不明な場合にはビームエキスパンダの出射部近傍でのビーム径を測定し、それをウェスト径の近似値として使用することができます。
ビーム広がり角
レーザ光のビーム径は、つねにウェスト部分で最小になります。ウェストから離れると、ビーム径は回折効果により大きくなりますが、伝搬に伴うその増加の割合がビームの広がり角に対応します。ビームウェストから遠く離れると、広がり角はほぼ一定になります(図4参照)。この広がり角(θ、単位:ラジアン)は、以下の式で表されます。

この値は、波長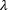 )
)
ビームエキスパンダまたはレデューサにおける入射ビームと出射ビームの広がり角の違いは、ビーム拡大率

で表されます。ここで、θin は入射ビームの広がり角、θoutは出射ビームの広がり角ですが、いずれもビームウェストから遠く離れた位置における値です。
ビームエキスパンダ(m > 1)の場合、出射ビームのウェスト径は入射ビームのウェスト径よりも大きくなり、出射ビームの広がり角は入射ビームの広がり角より小さくなります。出射ビームの広がり角が小さくなるため、ビームエキスパンダはアプリケーションで規定された最大ビーム径を超えることなく、自由空間光をより長い距離にわたって伝搬させるのによく用いられます。
ビームレデューサ(m < 1)の場合は、入射ビームよりも小さなウェスト径と大きな広がり角の出射ビームが得られます。その結果、出射ビーム径はビームレデューサの出射部近傍では小さくなりますが、光の伝搬に伴いビーム径は入射ビームよりも急速に大きくなります。ビームレデューサを使用する場合、光軸に沿ってビーム径をチェックし、ビーム径がアプリケーションにおいて許容される最大ビーム径を超えないことを確認することが重要です。
ビームのクリッピング防止
ビームエキスパンダ近傍の出射ビーム径は、多くの場合、出射ビームのウェスト径の良い近似値になっています。ビームエキスパンダから遠く離れるとビーム径は大きくなり、ビームのクリッピングやその他の予期しない影響が生じる恐れがあります。ビーム径
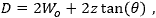
出射ビームのウェストからの重要な距離
最終更新日:2021年8月23日
Content improved by our readers!
ビームエキスパンダまたはレデューサの設計方式(ケプラー式、ガリレイ式)とその特徴
ビームエキスパンダまたはレデューサの設計方式が常にそのアプリケーションに影響を与えるわけではありません。しかし、例えばケプラー式のアライメントしやすさや直感的な設計、ガリレイ式のコンパクト性など、幾つかの要因は方式を選択するのに影響する場合があります。また、ケプラー式では2つのレンズの間で光を集光し、反転したビームを出射します。ガリレイ式ではビームを反転させず、またユーザはレンズを選択して出射ビームの球面収差を低減させることができます。
ビームエキスパンダとレデューサは、一般に発散光ではなくコリメート光にのみ使用され、またこれらの設計はケプラー式およびガリレイ式の望遠鏡から着想を得ています。どちらのデバイスも、倍率は出射側レンズの焦点距離を入射側レンズの焦点距離で除した値に等しくなります。
Click to Enlarge
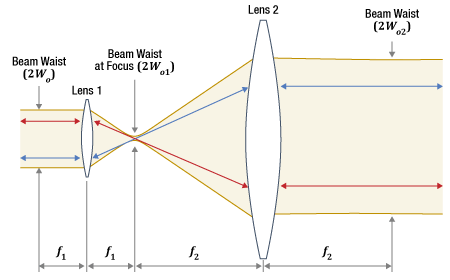
図5:ケプラー式の最もシンプルなビームエキスパンダまたはレデューサは、2枚の正レンズで構成されます。レンズ1の焦点距離はf1、レンズ2の焦点距離はf2です。レンズは2つの焦点距離の和に等しい距離
Click to Enlarge
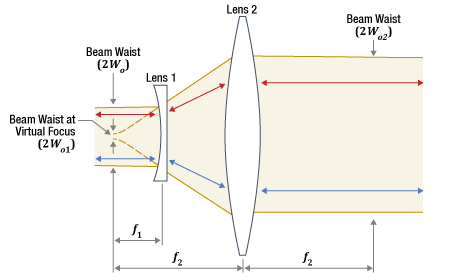
図6:ガリレイ式の基本的なビームエキスパンダまたはレデューサは、焦点距離が
ケプラー式の特徴
ケプラー式の最もシンプルな設計では、2つの正レンズがそれぞれの焦点距離の和に等しい距離だけ離れて配置されます(図5)。ケプラー式望遠鏡をベースにした設計では、その長さは2枚のレンズの焦点距離の和より短くなることはなく、また出射ビームは入射ビームに対して反転されます。
ビームは2つのレンズの間で集光されます。これにより、ビームを空間的にフィルタリングすることができます。例えば、ピンホールフィルタをビームの焦点位置に配置してビーム品質を向上させることができます。焦点から離れて出射側レンズに近づくにつれて、ビーム径は大きくなります。出射側レンズからのコリメート光の径を大きくするためには、出射側レンズを焦点からより遠く離す必要があります。焦点と出射側レンズの距離は出射側レンズの焦点距離と等しくなければならないため、焦点距離の長いレンズを使用する必要があります。
ケプラー式は、切断や加工などに使用される高出力パルスレーザなどの高エネルギービームには、一般に適していません。例えば、ナノ秒のパルス幅で1 MW程度以上の光パワーを有するビームを集光すると、空気がイオン化して火花が発生することがあります。これにより、パルスパワーが低下し、ビーム品質を低下させる可能性があります。
ガリレイ式の特徴
ガリレイ式の基本的な望遠鏡にも2枚のレンズが使われますが、1枚は負レンズでもう1枚は正レンズです(図6)。これらのレンズは、レンズ間の距離が焦点距離の差になるように配置されるため、ケプラー式よりもコンパクトになります。
ガリレイ式は、ビームエキスパンダやレデューサによって生じる球面収差を最小限に抑えるためにも使用されます。すべての球面レンズでは球面収差が生じ、これによりビームの焦点が光軸に沿って広がってしまいます。正の球面レンズの場合、レンズの外周近傍に入射する平行光線は、レンズの中心近傍に入射する平行光線と比較して、レンズにより近い光軸上の点に集光します。負の球面レンズにはこれと反対の効果があります。ガリレオ式では負レンズが使用されており、これにより正レンズによって生じる球面収差の一部を相殺することができます。
デバイスをビームエキスパンダとして使用するときは、径の小さなビームを負レンズ側に入射します。負レンズから発散する光は、2枚のレンズの間で集光することはなく、正レンズに近づくにつれてその径は大きくなります。この発散ビームは負レンズの反対側に虚焦点を有するものとみなすことができます(図6参照)。正レンズはこの虚焦点から正レンズの焦点距離
拡大率
ビームエキスパンダおよびレデューサは、コリメート光を入出射させます。ビームはコリメートされていても、伝搬時にビーム径は回折効果により変化します。入射ビームのウェストは入射側のレンズからその焦点距離だけ離れた位置にあるのが理想的です(図5、6参照)。次に、出射ビームのウェストは出射側のレンズからその焦点距離だけ離れた位置になります。入射ビームのウェストが入射側レンズからその焦点距離の位置にない場合、出射ビームのウェスト位置、ウェスト径および/または出射ビームの発散は、推定される値と一致しません。
ビームのウェスト径
デバイスが2枚のレンズで構成されている場合、ビーム拡大率を計算する式はケプラー式もガリレイ式も同じです。拡大率は、出射側レンズの焦点距離を入射側レンズの焦点距離で除した値に等しくなります。図5および図6のデバイスでは、光が焦点距離f1のLens 1に入射する場合はビームエキスパンダになります。この場合、2枚目のレンズ(Lens 2)の焦点距離はf2で、ビーム拡大率

図5および図6のデバイスをレデューサとして使用する場合は、Lens 2に光を逆方向から入射します。この場合はLens 1が出射側レンズになり、ビーム拡大率はf1をf2で除した値m21 になります。
最終更新日:2020年7月2日
Insights:光学実験のベストプラクティス
スクロールするか下のリンクをクリックすると、実験室での実習時のヒントや機器セットアップ時の注意点等がご覧いただけます。
- テーブルクランプ:保持力を最大にする方法
- 光学テーブル:テーブルクランプとテーブル面の歪みについて
- ワッシャ:オプトメカニクスに使用する場合
- 電気信号:AC結合 vs DC結合
- ファイバーコリメータ:アダプタを使って取り付ける場合
- 移動ステージ中央の大きな取付穴はどのように使用するか
- 直線ステージ取付けスロットの使い方
- 低パワー光検出方法を改善する最初のステップ
テーブルクランプ:保持力を最大にする方法
Click to Enlarge
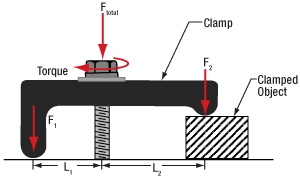
図 2:L1 > L2であるため、物体を保持する力は負荷した力(FTotal)の半分よりも大きくなります。クランプCL2/Mの左側の脚の長さは、物体の高さにあわせて調整可能です。そのためクランプの上面と取付け面を平行にすることができます**。
Click to Enlarge
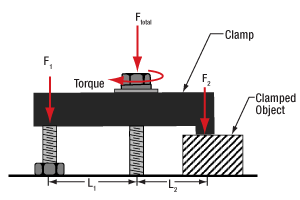
図 1:L1 < L2であるため、物体を保持する力は負荷した力(FTotal)の半分よりも小さくなります。上のクランプはCL5Aです。
クランプのスロット内の締め付けネジの位置が物体から離れすぎていると、クランプされている物体は動きやすくなります。ネジの位置を適切にすることにより、クランプされた物体の位置ずれを防止することができます。
クランプ力を最大化するためには、ネジをできるだけ物体の近くに配置してください**。
これは、CL5A(図1)やCL2/M(図2)のようなクランプを用いた場合、トルクのかかったネジによって加わる力(FTotal)は2点に分配されるためです。
クランプ力F2が物体にかかります。F2の値がFTotalの何%になるかは、以下で説明するようにL1とL2に依存します。残りの力(F1)は、クランプの反対側の端にかかります。
これらの2つの力は、次の式によって求められます。
 | もう一方の接点にかかる力: | 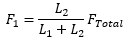 |
これらの式は、物体とネジ間の距離が小さくなると物体にかかるクランプ力が大きくなることを示しています。L1とL2が等しいとき、締め付けられたネジによってかかる力は、F1とF2に等しく分配されます。
**クランプ力を最大化するには、図1および図2に示すように、クランプの上面と物体に接触する面のどちらも、取付け面に対して平行でなければなりません。
クランプと物体間の接触面が取付け面に対して平行ではない場合、物体にかかる力は、物体を取付け面に押し付ける力と、取付け面に沿う方向に押す力とに分解されます。取付け面に沿う方向の力は、物体を移動せるのに十分な場合と、それほどではない場合があります。
物体の高さに対応させるために、CL2/Mのようなクランプではその一端の脚がネジになっており、高さ調整が可能になっています(図2参照)。クランプと取付け面の間のネジ山の数は物体の高さに応じて調整しますが、同時にクランプの上面が光学テーブルに対して水平になるように調整する必要があります。
最終更新日:2019年12月4日
1
光学テーブル:テーブルクランプとテーブル面の歪みについて
Click to Enlarge
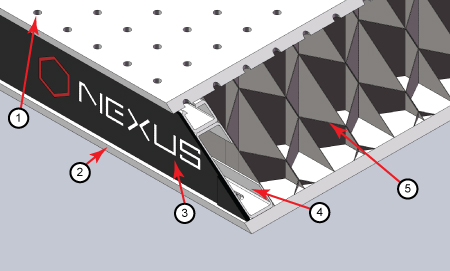
図3:Nexusテーブル/ブレッドボードの断面図。(1)上板、(2)下板、(3)サイドパネル、(4)サイドレール、(5)ハニカムコア。ステンレススチールの上板と下板の厚さは5 mmです。
Click to Enlarge
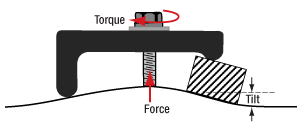
図5:ネジにトルクをかけるとテーブルの上板を上方向に引っ張る力が発生します。上に引っ張られた板が取付け面を傾けるため、物体に角度偏差を生じさせる可能性があります。上の図では、分かりやすくするために誇張して示しています。
Click to Enlarge
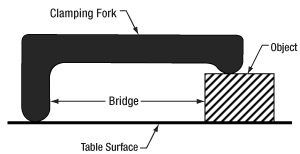
図4:CL5Aのような標準的なテーブルクランプでは、一端のみがテーブル面に接触します。反対の端は固定する物体と接触します。 2つの端の間にはブリッジ(隙間)が形成されます。クランプ力を加えるネジは表示されていません。

Click to Enlarge
図6:クランプアームPOLARIS-CA1/Mには取付けネジを挿入するスロットと、取り付けるポストを固定するためのネジが付いています。また、上面と底面は同じ形状です。クランプアームが取付け面と接触する面はほぼループ状につながっているため、ブリッジ(隙間)による影響はほとんど生じません。
テーブルクランプ(クランプフォークも含む)は、複合構造の光学テーブルの取付け面よりも剛性が高くなっています。ネジに加えるトルクを大きくしていくと、その力でテーブルクランプの背の部分が曲がると想像するかもしれません。しかしネジがテーブルクランプを変形させる前に、テーブルの上板を上に引っ張るため、上板がフラットではなくなります。そのためコンポーネントを光学テーブルに固定する際、テーブルクランプは慎重に使用しなければなりません。クランプアームはテーブルクランプの代わりにご使用いただけるもので、下記の説明の通り、テーブルの取付け面を変形させにくい製品です。
光学テーブルの構造
複合構造の光学テーブルとブレッドボード(図3参照)は、振動を減衰させながら剛性の高い構造となるよう設計されています。厚さ5 mmのステンレススチール製の上板はフラットな面となるよう製造されていますが、局所的な力が加わると変形する可能性があります。上板が変形すると光学部品は水平に設置できなくなり、光学系のアライメントや性能に悪影響を及ぼす場合があります。
テーブルクランプ
標準的なテーブルクランプは、一端がテーブル表面上に、もう一端は物体上に置かれます(図4)。この2つの端の間には、テーブル表面からクランプまでの隙間が生じます。このブリッジ(隙間)により、1本のネジでクランプをテーブルに固定すると同時に、物体を保持する力を発生することができます。
ネジにトルクをかけることによってクランプを固定するとき、ネジはテーブルの上板を上方向に引っ張ります(図5参照)。
ネジにかけるトルクをさらに大きくすると、テーブルの上板が上に持ち上がります。テーブルの上板が持ち上がることはテーブルに恒久的なダメージを与えるリスクがあるだけでなく、クランプで固定している光学部品のアライメントも乱してしまう場合があります。テーブルの上板が持ち上がると、クランプされている物体の下の取付け面は傾きます。
クランプアーム
POLARIS-CA1/Mなどのクランプアーム(図6参照)は、取付け面の変形を最小限に抑制しながらポストを固定するように設計されています。
図6のクランプアームと、テーブルクランプには2つの大きな違いがあります。1つは光学テーブルに接触する面(赤で表示)で、もう1つはポストを固定する方法です。
光学テーブルに接触する面(クランプのベース周り)は、ほぼループ状につながっています。クランプをテーブルに取り付けたときの接触面は、テーブルに対してフラットな平面になります。ループとして不連続な部分は、ポストをグリップするための幅の狭いスロットのみです。
テーブルクランプで使用するネジは1本だけですが、この設計では2本のネジを使用します。1本のネジ(表示されていません)でクランプをテーブルに固定し、もう1本のネジ(表示されています)でポストをグリップします。1本のネジが両方の機能を果たす必要がないため、クランプする物体と光学テーブルの間のブリッジ(隙間)は必要なくなります。
クランプの接触面はループ状で、全表面が接触しているわけではありませんが、取付け面の変形はほとんど無視できる程度です。これは接触面の内側の空洞の部分が狭く、またクランプの両サイドで囲まれているため、テーブルを上に引っ張る力に対して抵抗できることによります。
最終更新日:2019年12月4日
2
ワッシャ:オプトメカニクスに使用する場合
Click to Enlarge
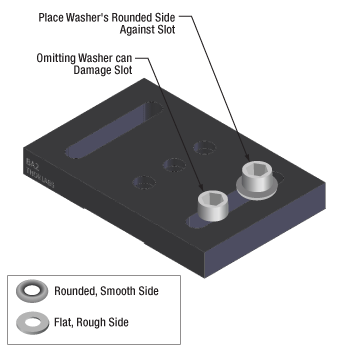
図8:スロットを損傷させないよう、ボルトを挿入する前にワッシャを入れてください。ワッシャの丸みを帯びた滑らかな面をスロット側に向けて置き、フラットな粗い面がボルト頭部と接触するようにします。滑らかな面は、アルマイト処理された表面を傷つけることなく、容易に移動できるように設計されています。上の図はベースBA2(/M)です。
Click to Enlarge
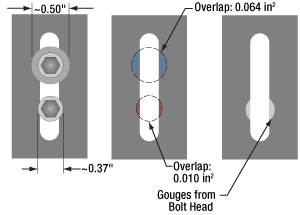
図7:ワッシャの直径はボルト頭部より35%大きくなっています。これによりベースBA2/Mのスロットにオーバーラップする面積はボルトの6倍になります。ワッシャはボルトの力をより広い面積に分散することで、スロットがえぐられるのを防止する役目をはたします。
標準的なキャップスクリュの頭部は、ネジの外径よりもそれほど大きくはありません(図7)。例えば1/4-20"ネジの頭の径は0.365~0.375インチ(約9.27~9.53 mm)で、このネジ用の貫通穴の径は0.264インチ(約6.71 mm)です。
デバイスを固定するためにネジを直接貫通穴に入れて締め付けると、力が貫通穴のエッジ部分にかかり、ネジでデバイスのエッジ部分をえぐってしまう場合がよくあります(図7)。
このエッジ部分が恒久的に変形してしまった場合、ネジの頭はえぐられた溝に戻ろうとするため、デバイスを精密に調整しようとしても、デバイスは元の位置に戻ってしまいます。
円形の貫通穴の場合は、ネジに対してデバイスを移動させようとするものではないので、このような変形による問題は生じないことが期待できます。
しかしスロットの場合には、スロットに沿ってどの位置にでもデバイスを固定できなければなりません。ワッシャを使用すると、力がスロットのエッジから離れる方向に分散されるので、スロットが変形しにくくなります。図7では、ワッシャがもたらす効果を図示しています。ベースBA2/Mのスロットと頭の径が0.37インチ(約9.4 mm)のキャップスクリュの接触面積は0.010 in2(約6.5 mm2)です。径0.5インチ(12.7 mm)のワッシャを使用すると接触面積は0.064 in2(約41.3 mm2)となり、6倍ほど大きくなります。
当社のワッシャには、それぞれの面に特徴があります(図8)。1つの面はフラットで粗く、もう1つの面は丸みを帯びていて研磨されています。丸みを帯びた研磨された面を、アルマイト処理されたデバイスの面に向けて置いてください。
ネジを締め付けるときに、ネジの頭でワッシャがアルマイト処理された面に対して回転する場合があります。
フラットで粗い面をアルマイト処理された面に押し付けた場合、摩擦でその表面を傷つける場合があります。しかし、丸みを帯びた面を接触させた場合、滑らかな面による摩擦は小さいため傷がつきにくく、デバイスの外観がより長く保たれます。
最終更新日:2019年12月4日
3
電気信号:AC結合 vs DC結合
Click to Enlarge
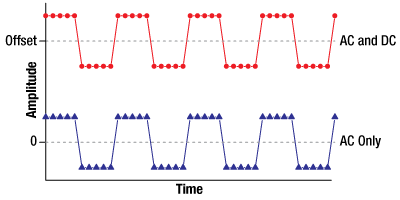
図9:信号のDCオフセットは信号の平均値です。青い線(ACのみ)の平均振幅は0なので、DCオフセットはありません。赤い信号(ACとDC)は、赤い信号のACオフセットが0ではないこと以外、青い信号と同一です。DC結合は赤い信号を変化させることなく通過させます。AC結合ではDCオフセットを除去し、信号の低周波成分を減衰させます。
機器にAC結合とDC結合の電気入力の選択肢がある場合、変調信号入力に対して、DC結合の方がよい選択であることが多々あります。
AC結合とDC結合
AC結合とDC結合は、入力信号と、機器のその他の電気回路の間のインターフェイスです。
DC結合は直流結合で、本質的にワイヤが信号の入力部に接続しています。この導電結合は直流成分と交流成分である信号の周波数成分すべてを伝送します。図9の赤い線の直流成分は0ではありません。
AC結合の主な特長はコンデンサを信号入力部に対して直列に配置することです。コンデンサはハイパスフィルタとして機能し、阻止コンデンサと呼ばれることもあります。AC結合ではDCならびに低周波成分が大きく減衰されます。このような静電結合は、入力信号からDCオフセットを除去し、AC成分のみを通過させるために使用されます。図9の青い線にはAC周波数成分しかありません。
可能な場合、DC入力をご使用ください
DC入力が好ましい理由は多くあります。低周波数応答性が良く、信号のDC成分をAC成分とともにモニタでき、また信号の周波数成分に影響を及ぼさないため、信号の歪みを生じさせません。
DCオフセットが大きいか、AC入力によるフィルタリングが必要な場合を除き、DC入力をお勧めいたします。DCオフセットが大きいことの問題の1つは、機器の分解能よりも低いレベルまで下げる場合があることです。極端なケースにおいてはDCオフセットにより光のクリッピングや飽和効果が生じる場合があります。
なお、DC入力であっても、信号の歪みがないことは保証されませんのでご留意ください。歪みはデバイスの帯域幅の不足や、終端でのインピーダンスの不一致などほかの理由で起こる場合があります。
Click to Enlarge
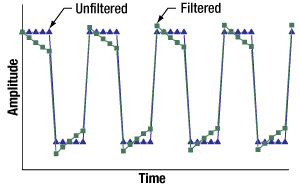
図 11:上のグラフの青い曲線のように変調信号によってはDC成分がなくても、少なくない量の低周波成分は存在します。この信号がAC結合のハイパスフィルタによってフィルタイングされると、結果信号に歪みが生じます。緑の線はその1例です。
Click to Enlarge
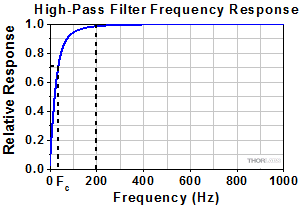
図 10:コンデンサがベースのハイパスフィルタの周波数応答性をモデル化しています。カットオフ周波数(Fc)は35 Hzで、図11の信号のフィルタリングに使用されました。信号の繰り返し周波数は 200 Hzです。
AC入力を使用する理由
AC結合は信号のDC成分を阻止することにより、信号の全体の振幅を減少させることができます。これにより、機器の測定分解能を向上することができ、また飽和やクリッピングの問題も克服できます。情報伝送を高周波成分で行う場合、そして低周波成分に関心がない場合、AC結合は良い結果をもたらします。また一部の通信用途などDCの周波数成分が容認されない用途においてはAC結合が好ましい場合があります。
AC入力を使用する場合
AC結合を使用した場合、AC結合がハイパスフィルタとして機能し、信号の周波数成分に影響を及ぼすことを念頭におくことが重要です。
図10で示すように、AC結合はDCオフセットを除去するだけでなく、関心のある低周波成分も減衰させる場合があります。AC結合は結果、信号の歪みにつながる場合があります。ハイパスフィルタの影響を説明するため、図11では繰り返し周波数が200 Hzのバイナリ信号を、カットオフ周波数(Fc)35 Hzのハイパスフィルタでフィルタリングする前と後のグラフを示しています。
AC結合のデジタル通信信号では、DCオフセットのないDCバランスのとれた信号を使用することによりこの問題を軽減しています。信号のDCバランスが取れていない場合、一連の信号は高い信号レベルに張り付いてしまう場合があります。これにより、信号が静電フィルタリングの影響を受け、non-zeroのDCレベルが生じることがあり、その結果、ビットエラーをもたらされます。
最終更新日:2019年12月4日
4
ファイバーコリメータ:アダプタを使って取り付ける場合
Click to Enlarge
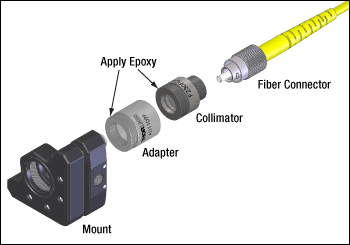
図12:上の図では各コンポーネントをネジで結合しています。ファイバーコネクタのネジを緩めると、意図せずほかの部品同士の接続まで緩めてしまう場合があるため、当社ではほかの2箇所の接続部を接着剤で固定することをお勧めしています。
ファイバーコリメータは、ファイバ出力型光源から光学系に光を入射するときによく使用されます。当社では様々な種類のファイバーコリメーターパッケージをご用意しております。その一部のパッケージはネジの無い滑らかなバレル(トリプレットコリメータなど)になっていますが、ほかにはバレルの先端にミリ規格のネジ(非球面コリメータなど)が付いているものがございます。
通常当社では、どちらのパッケージにも、バレルを2線接触で保持するタイプの、先端がナイロン製の止めネジ(セットスクリュ)が付いたアダプタの使用をお勧めしております。
一方、ファイバーコリメータをマウントにねじ込むことができる、外ネジ付きのアダプタ(AD1109F)もございます。
しかし、このようなアダプタを使用した場合、ネジによる接続が重なってきます(ネジ付きファイバーコネクタ、ネジ付きコリメータ、そしてネジ付きアダプタ)。その結果、ファイバーコネクタを緩めるときに注意しないと、その他のネジによる接続部分まで緩めてしまい、セットアップに原因不明な不安定性が生じる場合があります。
そのため、このような取り付け方をしたい場合には、当社ではネジ付きファイバーコリメータとネジ付きマウントを接着剤で固定することをお勧めしています。
最終更新日:2019年12月4日
5
移動ステージ中央の大きな取付穴はどのように使用するか
移動ステージには、ステージの周辺よりも中央寄りの位置に、光学テーブルやブレッドボードへの取付け穴が配置されているものがあります。そのようなステージの場合、取付け面に固定したり外したりする際に、上部プレートを下部(ベース)プレートの中心に合わせる必要があります。そのとき、上部プレートの大きな貫通穴と下部プレートの小さな貫通穴は1つのザグリ穴のような形になります。
その状態でキャップスクリュを上部プレートの大きな穴から挿入し、取付け面にねじ込んでステージを固定します。ここでは直線移動ステージMT1B(/M)を用いてその方法をご紹介しています。ステージを取り外すときは、同じ穴を使用してネジを緩めて外します。

Click to Enlarge
図14:ステージ上部プレートの2つの大きな貫通穴から、ステージ下部プレートの取付け穴を利用することができます。

Click to Enlarge
図13:ステージ下部プレートの中央付近の貫通穴は、ステージを光学テーブルやブレッドボードに固定するための取付け穴です。
動画1:直線移動ステージMT1B(/M)を光学テーブルに固定する手順

Click to Enlarge
図15:ステージ上部プレートの大きな貫通穴から5 mmボール(六角)ドライバを差し込み、挿入したM6キャップスクリュを締めてステージを固定することができます。
取付け穴の位置について
取付け穴(図13)は下部プレートに開いている貫通穴で、この下部プレートがテーブルに固定されます。取付け穴の径は、M6キャップスクリュのネジ部分は通しますが、頭部分は通さない大きさです。この取付け穴は、ステージの可動部である上部プレートの大きな貫通穴(図14)から利用します。
しかし、取付け穴を利用するには、上部プレートと下部プレートの位置を合わせる必要があります。アジャスタで上部プレートの位置合わせを行いますが、このとき上部プレートの大きな貫通穴と下部プレートの小さな貫通穴の中心を一致させ、ザグリ穴のような形にします。キャップスクリュをネジの部分から上部プレートの貫通穴に挿入すると、ネジはスムーズに下部プレートの取付け穴に入ります。
最初にステージを固定してからコンポーネント類を取り付けてください
上部プレートと下部プレートの位置合わせができたら、下部プレートを取付け面側に向けて、ステージを光学テーブルまたはブレッドボード上に置いてください。ザグリ穴状態の2つの貫通穴と取付け面のネジ穴を合わせ、ステージの上から貫通穴を通してM6キャップスクリュを挿入し、光学テーブルに締め付けてください(図15)。
上部プレートは下部プレートに対して移動するため、使用しているときは一般に上部プレートが妨げになって取付け穴のネジは操作できません。また、ステージに取り付けたコンポーネントにより、概して上部プレートの貫通穴の一方または両方が塞がれてしまいます。そのため、実験の途中でステージの取付け位置を変更することには不便が伴う場合があります。従って、コンポーネント類をステージに取り付ける前に、ステージを適切な位置に固定することを推奨します。
他の選択肢として、MTシリーズ用のMT401/Mのようなベースプレートを使用すれば、ステージの周囲に塞がれることのない取付けスロットを確保できます。ステージをここで説明したようにベースプレートに固定してから、ベースプレートの取付けスロットを使用して取付け面に固定します。
取付け方法を動画でご覧ください
取付け方法は動画1でご覧いただけます。またこちらの動画ページ では、アジャスターネジを電動アクチュエータに交換する方法など、移動ステージに関する他の情報もご覧いただけます。
最終更新日:2020年9月8日
直線ステージ取付けスロットの使い方
直線移動ステージの下部プレートの4隅に取付けスロットがある場合、通常そのうちの2つ以上の取付けスロットは上部プレートに妨げられて使用することができません。素早く4つの全てのスロットを使用するには、まずマイクロメータまたはアクチュエータで上部プレートを手元側に引き寄せて2つの取付けスロットを露出させ、次に上部プレートを逆方向に手で押し出して他の2つの取付けスロットを露出させる方法があります。そうした後、ロッキングプレートの固定ネジを締めて上部プレートの位置を固定します。ここでは直線移動ステージXR25P(/M)を用いてその方法をご紹介しています。

Click to Enlarge
図 17:この写真では、マイクロメータの反対側の側面に付いている長方形のスロット付きロッキングプレートが見えています。また、手前の2つの取付けスロットは露出していますが、後ろ側の2つの取付けスロットは上部プレートに覆われて利用できない様子も見えます。

Click to Enlarge
図16:上部プレートがマイクロメータで最も引き寄せられたとき、ステージの片側の2つの取付けスロットが露出して利用できるようになります。どちらのスロットにもM6キャップスクリュとワッシャを取付けられます。ステージの反対側の2つの取付けスロットは、上部プレートに妨げられて利用できません。
動画2:直線移動ステージXR25P(/M)を光学テーブルに固定する手順

Click to Enlarge
図18:上部プレートを引き寄せた位置から最も押し出した位置まで移動させると、他の2つの取付けスロットが露出して利用できるようになります。ロッキングプレートのネジを2 mm六角レンチで締め付けて、上部プレートの位置を固定します。
2つの取付けスロットが利用できるように上部プレートを移動させる
ステージを光学テーブルやブレッドボードに固定するための4つのザグリ穴スロットは、ステージの下部(ベース)プレートに付いています。上部プレート(可動部)が下部プレート(固定部)の中心に位置しているときは、4つの全ての取付けスロットが上部プレートに妨げられて利用できません。上部プレートが最も引き寄せられた位置か最も押し出された位置にあるときには、取付けスロットが2つずつ露出して、それぞれを利用することができます。
4つの全てのスロットを素早く利用するには、まずマイクロメータやその他のアジャスタを使用して、上部プレートを手元側の位置に引き寄せます。そうすることで2つの取付けスロットが露出し、M6キャップスクリュとワッシャを締めたり緩めたりすることができます。図17でご覧いただけるように、上部プレートがこの位置にあるときは、ステージの反対側の取付けスロットは上部プレートに妨げられて利用できません。
ほかの取付けスロットを利用するために上部プレートを手で押して固定します
下部プレートを固定し、上部プレートを手元側に最も引き寄せた状態にして、上部プレートをバネの力に対抗して手で押し、最も押し出した位置まで移動させます。 このとき上部プレートから手を離さないでください。手を離すと上部プレートがバネで引っ張られ、ストッパに衝突してステージが破損する場合があります。
上部プレートは、下部プレートのもう一方の取付けスロットが露出する位置まで押してください。次にロッキングプレートのネジを締め付け(図18)、上部プレートの位置を固定します。上部プレートを固定したら、露出した取付けスロットへのM6キャップスクリュとワッシャの取付け・取外しが可能になります。
ステージを破損させないために
ロッキングプレートのネジを緩めるときは、バネで上部プレートが戻らないように手で押さえてください。上部プレートが静止する位置で手をそっと離してください。上部プレートがストッパに衝突すると、その衝撃でステージ部品のミスアラインメント、ボールベアリングへのダメージ、あるいはステージの移動時における角度偏差などが生じる場合があります。
手順は動画をご覧ください
手順は動画2でご覧いただけます。また、こちらの動画ページでは、アジャスターネジを電動アクチュエータに交換する方法など、移動ステージに関する他の情報もご覧いただけます。
最終更新日:2020年9月8日
低パワー光検出方法を改善する最初のステップ
低パワーの光信号の測定は、周囲光の低減、パワーセンサ(フォトセンサ)に入射する反射光や散乱光の遮断、ビームスポットサイズの適正化(センサの受光面サイズ以内にする)、パワーメータのダイナミックレンジの適切な設定、および周囲光下でのパワーメータのゼロ設定などで改善することができます。ここで目標とするのは、パワー測定での不要な光の影響を最小限に抑えることと、センサがビーム全体のパワーを連続して測定すること、そして実験条件に応じてパワーメータを適切に設定することです。
周囲光
周囲光とは、光学系における光ビーム以外のすべての光を指します。多くの場合、室内光が最大の周囲光になりますが、かなりの光がPC画面や他のモニタ画面、機器のLEDインジケータなどで生じている場合もあります。周囲光で困る点は、測定中に使用者が移動したり、インジケータの点滅や画面表示を切り替えたりしても光の量が変動することです。
周囲光の影響により、パワーの読み取り値が不自然に上昇したり、低パワー光の検出の妨げになったり、あるいはセンサを飽和させたりすることがあります。センサが飽和すると、センサは最大レベル、またはそれに近い信号を出力します。周囲光によって飽和したセンサでは、周囲光に付加されるた入射光パワーに応答できないか、あるいはほとんど応答できない状態になります。周囲光が飽和しない程度の低いレベルであっても、検出しようとする信号光が周囲光に比べて無視できるほど小さい場合には、やはり検出できません。

Click to Enlarge
図19:上のセットアップでは、ネジ変換アダプタSM1A29を用いてSM1レンズチューブをパワーセンサS130Cに取り付けています。パワーセンサは、レンズチューブの開口部が直近の光学部品の透過側にほぼ接触するように配置されています。レンズチューブはパワーセンサを不要な光から遮蔽するのに寄与します。このセットアップは、こちらの動画で直線偏光子を入射面に対して45°にアライメントする方法の実演に使用されました。
Click to Enlarge
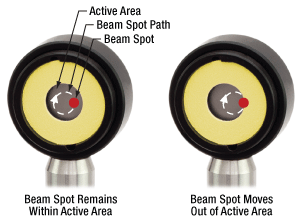
図21: ビームスポットは、アライメントの状態や通常の動作状態においてもパワーセンサ内を移動する場合があります。光パワーを正確に測定するには、ビーム全体がパワーセンサの受光面内になければなりません。上の図では、測定中にビームスポットが円状に移動する様子を白い点線の円で描いています。ビームスポットがセンサの受光面内に留まるのが理想です(右)。ビームがパワーセンサの受光面から外に出てしまう場合(左)は、パワーの読み取り値が不自然に小さくなる理由を説明するのが困難になります。
Click to Enlarge
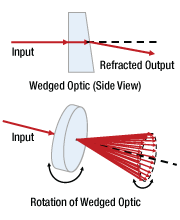
図20:上の光学素子の前面と背面は平行ではありません。光学素子を光軸周りに回転させると、透過ビームの方向が変化します。このような状況では、光パワーの測定が不正確になる場合があります(図21参照)。
周囲光を最小に抑えるには、室内光を消す、遮光機能付きのエンクロージャ内にセットアップを設置する、モニタにカバーをかける、スクリーン画面をセンサとは反対側に向ける、LEDを消灯するか黒色テープで覆うといった対策がとれます。図19のようにセンサの筐体にレンズチューブを取り付けるのは、パワーセンサに入る周囲光を低減するのに効果があります。
迷光
光学系内のビーム光は、セットアップ内の光学素子や筐体による散乱、反射、回折などを通じて、迷光を発生させる場合があります。迷光は様々な光学素子から複数回の影響を受けていたり、主光路とオーバーラップしたりするため、その光路を予測したり遮断するのは難しい場合があります。信号測定に対する迷光の影響は、周囲光の影響と似ています。
迷光を遮断する最良の方法はビームの光路とセットアップに依存し、複数の技術が組み合わされて使用されます 光路を辿らずに迷光を除去できれば、それが最も簡単です。光学面を入射ビームが垂直に入射しないように回転させれば、反射光を光路以外の方向に向けることは可能です。しかしこの方法は、光学素子への入射角が実験に影響を与えない場合にしか使用できません。
信号光と迷光の光路間の角度が比較的大きい場合には、センサにレンズチューブを取り付けることで(図19)迷光を遮断することができます。信号光と迷光の光路間の角度が小さい場合には、1つの方法として、センサの前にアイリスを配置して迷光を遮断し、信号光のみを通過させる方法があります。もう1つの方法としては、センサを遠ざける方法があります。十分な距離があれば、信号光と迷光の間の距離が大きくなり、迷光がパワーセンサに入射しなくなるか、またはパワー測定にほとんど影響を与えなくなります。
パワーセンサのサイズとビーム変位(ビームウォーク)の許容範囲
信号光の直径がパワーセンサの受光面の直径より大きい場合、信号光の測定値は不自然に小さくなります。なお、ガウスビームの一般的な測定値として規定されている1/e2ビーム径には、光パワーのおよそ86%が含まれています。光パワーの99%を含む直径は、1/e2ビーム径より1.5倍大きくなります。
ビームはセンサ受光面の中心にアライメントされているのが理想です。ビームがセンサの中心にない場合は、測定誤差のリスクが増大します。ビームスポットがセンサの受光面の外にまで広がっている場合は、パワーの測定値は小さくなります。ビームの一部分が受光面とオーバーラップしているときには、パワーがある程度測定されているため、すぐに問題があることに気づかないかもしれません。そのため、測定する前にビームスポットと受光面のオーバーラップの具合を確認することをお勧めします。
このビームスポットと受光面の不完全なオーバーラップの問題は、測定中にビームスポットが移動するときには、一時的な問題である場合があります。例えば、測定中に光学素子を光軸周りに回転させる必要がある場合は、ビームスポットも移動するかもしれません(図20と図21)。これは、光学素子の前面と背面が光路に対して垂直ではない場合に特に懸念されることです。ビームスポットが移動する場合には、受光面の大きなパワーセンサを選択することで対応できる場合があります。
パワーセンサのダイナミックレンジ
センサのダイナミックレンジは、センサが対応可能な入射光パワーの最小値から最大値までの範囲を指します。正確な測定をするためには、信号光パワーがセンサのダイナミックレンジ内であることが必要です。
ノイズフロアにより、一般に検出可能な光パワーの最小値が決定されます。ノイズフロアは、パワーセンサに光が全く入射されていないときにパワーメータで読み取られるパワー信号のことです。このパワー信号は、パワーセンサ、パワーメータ、ケーブル、増幅器、フィルタ、およびその他の全てのコンポーネントを含む検出器システム全体のノイズから生じるものです。ノイズフロア以上の応答を発生させるのに十分な入射光パワーがないと、信号としては検出されません。応答信号がノイズフロアに近いと、測定精度は低下します。ノイズフロアに近いレベルの信号では、小さな信号対雑音比(SNR)しか得られません。
パワーセンサのメーカでは、最大パワーの仕様値を、飽和強度と呼ばれる閾値以下にしばしば設定します。飽和強度の閾値よりも十分に低いレベルで使用することが推奨されるのは、パワーが閾値近くになるとセンサの応答が非線形になり、実際に入射されたパワーよりも小さな値を表示する場合があるからです。これにより、意図せずにアプリケーションで許容される最大パワーを超えてしまう事態も考えられ、これは極めて懸念すべきことです。入射光パワーが飽和強度を超えると、測定値はしばしば最大値に固定されることがあります。飽和状態かどうかを確認する方法の1つは、パワーを若干上げてパワーの読み取り値をモニタする方法です。読み取り値が一定であるか、予想ほど変化しない場合には、センサが飽和している可能性があります。
パワーメータのゼロ設定を周囲光レベルに合わせる
信号光がセンサに到達しないように遮断した状態で、センサを覆わずにゼロ設定を行います。信号光の遮断は、光源側に内蔵シャッタがあればそれを使用し、あるいは光源の前にビームブロックを直接置いて行います。ビームブロックをセンサに近づきすぎないよう置くことが重要です。なぜならゼロ設定時には、パワーセンサは測定中に存在するすべての周囲光に晒されている必要があるからです。この設定をすることで、周囲光の影響は測定値から差し引かれます。ゼロ設定時にセンサに覆いを付けてしまうと、周囲光のパワーが信号光の測定値に加算されます。
最終更新日:2022年5月16日
コリメート光は無限遠まで一定のビーム径を維持するか
理想的なのは、コリメート光の径がレンズの位置から無限遠まで一定であることですが、伝搬していくにつれ全く同じ径を維持するコリメート光は物理的に存在しません。コリメートビームの広がり角は、ビーム径が変化する割合を示しますが、光源とコリメータの両方の特性に依存します。そのため、ランプやLEDなど広帯域波長光源からのコリメートビームは、レーザなどの狭帯域波長光源からのコリメートビームとは異なるふるまいをします。
Click to Enlarge
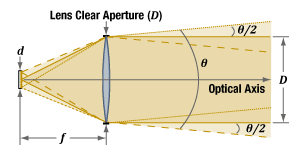
図1:ランプやLEDなどの広帯域波長光源を、レンズから焦点距離
Click to Enlarge
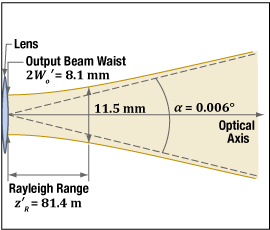
図3:図2の入射パラメータにより、レンズから焦点距離(50 mm)の位置にビームウェストがあるコリメート光が出射されています。なお、この図の尺度は図2より大きくなっています。ビームウェストの近く )
)
Click to Enlarge
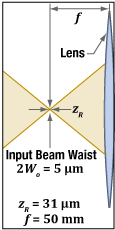
図2:ビームウェスト径(Wo)が5 µm、レイリー長(zR)が31 µmの632.8 nmレーザ光源が、焦点距離(f )50 mmのレンズによってコリメートされます。
Click to Enlarge
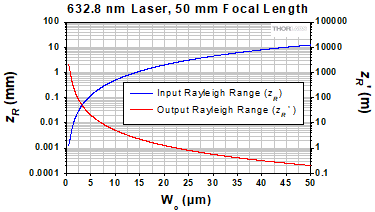
図4:入射光はビームウェスト径(Wo)が小さく、その結果レイリー長(zR)が狭いときに、点光源と見做すことができます。コリメートされた出射ビームのレイリー範囲(zR')は、Wo 、焦点距離、波長に依存します。焦点距離を長くするか、波長を短くすると、zR'は大きくなり、出射ビームの広がり角全体が小さくなります。上のグラフは、波長632.8 nm、焦点距離50 mmで計算されました。比較のため、波長1550 nm、焦点距離25 mmでの値も計算されています。
ランプまたはLEDからのコリメート光
理想的な点光源は全方向に均一な光を放射し、焦点距離
θ ~ d / f ,
この光源が理想的な点光源に近いほど、コリメートビームの広がり角は小さくなります(図1)。光源が小さいか、レンズから遠い位置にあるか、もしくはその両方のとき、その光源は理想的な点光源により近くなります。
十分な点光源と見做せるランプまたはLED
コリメートされた出射ビームの広がり角が用途の要件と合致したとき、その光源は理想的な点光源と見做すことができます。広がり角が大きすぎる場合、コリメートレンズの焦点距離を大きくして、光源を遠くに配置するという対策があります。しかし、これによりレンズに入射する光量、すなわちコリメートビームの出射光量が減少するというマイナス効果が出てしまいます。
図1では、光源の各点から放射された光がレンズの有効径いっぱいまで広がっています。光源の異なる点からの光線は異なる角度でレンズから出力するため、出射ビーム径はレンズ位置で1番小さくなることを示しています(レンズからの出力後、ビームがレンズの有効径から広がっています)。光源の各点からの光がレンズの有効径の一部のみにしか広がらない場合、ビームウェストはレンズからずれることになります。
点光源としてのレーザ光源
この点光源モデルはレーザ光にも適用できますが、この場合光源は入射ビームウェストと定義されます。光源のサイズはビームウェスト径
点光源モデルを当てはめるとき、レーザと広帯域光源では類似点があります。例えば、レーザ光源でもまた、コリメートビームの広がりを最小に抑えるために焦点距離だけ離れた位置にレンズを配置する必要があります。また、レーザ光源(入射ビームウェスト)が小さければ小さいほど、コリメートビームの広がりは小さくなります。
LEDやランプとは異なり、レーザ光源は広がりは大きいが、全方向に均一な光は放射しません。単波長レーザの光の場合、光軸と垂直な面における強度分布がガウス関数に似ています。その場合、コリメートビームのふるまいはガウシアンビームの式を用いて表すことができ、ビームの広がり角を表す式は波長を含む必要があります。
レーザのコリメート光
レーザ光源のサイズは、コリメートビームの特性を判断するのに役立ちます。サイズは通常、ビームウェストの半径
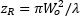 ,
,
ここで(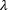 )は波長です。 入射ビームウェストが小さく、その結果、レイリー範囲も小さくなると、出射されるコリメート光の広がりは小さくなります。 (例示の図2と3をご覧ください。) コリメートビーム全体の広がりは、入射光のビームウェスト径を小さくすることで小さくなります。
)は波長です。 入射ビームウェストが小さく、その結果、レイリー範囲も小さくなると、出射されるコリメート光の広がりは小さくなります。 (例示の図2と3をご覧ください。) コリメートビーム全体の広がりは、入射光のビームウェスト径を小さくすることで小さくなります。
光源のビームウェストがレンズから焦点距離の位置にあるとき、コリメート光のビームウェストはレンズの反対側の焦点距離の位置にあります。ビームの広がりはビームウェストから離れると大きくなり、ビーム広がり角はウェストから近い領域または遠い領域で分けて表します。
ビームウェストの近くでは、出射ビームは理想的なコリメートビームに似ています。この領域では、ビーム広がり角は最小で、ビーム径は出射光のビームウェスト径
 .
.
用途によっては、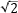 倍)となることを覚えておくと役立ちます。zR とzR'、入射ビームと出射ビームのレイリー範囲の異なる関係性については、それぞれ図4に示しています。
倍)となることを覚えておくと役立ちます。zR とzR'、入射ビームと出射ビームのレイリー範囲の異なる関係性については、それぞれ図4に示しています。
出射側のビームウェストから十分遠い位置にあると
 .
.
最終更新日:2021年4月20日
コリメートレンズから出射された光のビームスポットは、ランプまたはLED光源の像を形成するか
レンズがランプやLEDなどの光源から焦点距離の位置にあるとき、レンズは平行光線束のオーバーラップで構成された光を出射し、像は形成しませんがビームスポット(ビームウェスト)を形成する場合があります。光線束はそれぞれ異なる角度で出力するため、光軸と垂直面の強度は分布を持ちます。強度は光が集光しているように見えるビームスポット(ビームウェスト)位置で最も高くなります。しかし、各光線束は平行であるため、像は形成されません。ビームスポットの位置と径は、光源とコリメートレンズの光学特性に依存しますので、用途に適したビームスポットが得られるよう設計できます。
Click to Enlarge
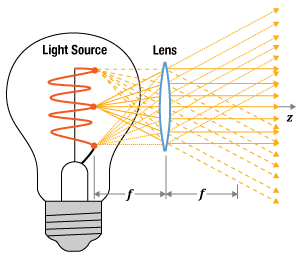
図6:光源からの光が大角度で放射されるとき、各点光源からの光線は、レンズの全表面積に入射されます。レンズは平行光線の束(各点から1つの光線束)を出射しますが、ビームスポット(ビームウェスト)はレンズの焦点距離先ではなく、レンズの出射面の位置になります。
Click to Enlarge
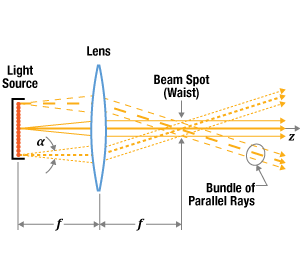
図5:レンズから焦点距離(f )の位置にビームスポットが得られているには、いくつかの要因があります。Z軸周りの光線の対称性や、各点光源からの出力光がレンズ全体まで広がらないことなどがこれに含まれます。レンズは各点光源から1つの光線束を出射しますが、各束の直径はレンズ径よりも小さくなります。光線束がオーバーラップすることでビームスポットが形成されます。
Click to Enlarge
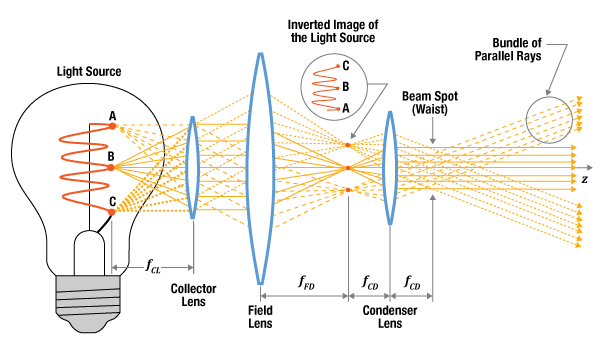
図7: 複数のレンズを用いればどこにでもビームスポットを形成することができます。こちらのケースでは、ビームスポットはコンデンサーレンズの出射面から焦点距離(fCD )の位置にあります。各点光源から放射される光線はビームスポットでは平行であるため、ビームスポットでは像は形成されません。なお、各点光源の逆さ像は、フィールドレンズとコンデンサーレンズの間で、フィールドレンズ視野レンズから焦点距離(fFD )の位置に形成されます。この例において、光源はコンデンサーレンズから焦点距離(fCL )の位置にあります。
ビームスポットで像は形成されません
図5の左側の光源は、放射点が垂直方向に並んでいます。これは一般的な光源ではありませんが、後述のとおりレンズを複数用いることで、このような特性を持つ光源を作ることはできます。
各点からの光線は小さな角度( )で広がっています。光は焦点距離(f )だけ離れた位置のレンズに入射されます。レンズは平行光線の束(各点光源につき1束)として光を出射します。
)で広がっています。光は焦点距離(f )だけ離れた位置のレンズに入射されます。レンズは平行光線の束(各点光源につき1束)として光を出射します。
各光線束は光軸(Z軸)を交差します。特定の点光源から放射された光の角度を知るには、まず点光源からレンズまでZ軸に平行な線をトレースします。この線はレンズ位置から、光軸(Z軸)上でレンズから焦点距離だけ離れた点に向かいます。この図では、これらの光線は各群の中心にあり、太い線で描かれています。
すべての平行光線束が交差することで、レンズから焦点距離先の位置でビームスポット(ビームウェスト)が得られます。ここで、出射ビーム径は最も小さくなり、強度は最も高くなります。しかし、ビームスポットでは光源の像が形成されません。なぜなら各束の光線は互いに平行だからです。光源の像を形成するには、各束がそれぞれ1点に収束しなければなりません。
ビームスポット(ビームウェスト)は常に得られるわけではありません
図5ではレンズから焦点距離の位置にビームスポットが得られていますが、これにはいくつかの理由があります。1つには光源がレンズから焦点距離だけ離れた位置にあります。2つ目には、光源から放射される光線群はすべてZ軸周りに対称であることです。さらに、各点からの光線の円錐はレンズ全体まで広がっていないため、出射される光線束の径は比較的小さくなります。
図6ではより典型的な白色広帯域光源を表しています。各点からの光線は大きい角度で放射されているため、光線はレンズの全面積に入射されています。このとき、ビームウェストの位置はレンズの出射面になります。
ビームスポットの設計
ビームスポットでの強度が最も大きくなり、光源の像が形成されないため、ビームスポットは均一照射に有用となります。光源の各点からの光が幅広い角度で放射され、レンズから遠い位置で均一に照射される必要があるときには、複数のレンズを用いることがあります。
図7ではレンズ系の代表例を示しています。コレクターレンズが平行光線の束を出射し、ビームスポットは図7のとおりコンデンサーレンズの出射側にあります。フィールドレンズはコレクターレンズから出射された各光線束を集光します。光源の上下反転像が、フィールドレンズとコンデンサーレンズ両方からそれぞれの焦点距離だけ離れた位置に形成されています。この反転像からの光線は、コンデンサーレンズの入射面の一部に入射されているため、このレンズから出射された光は焦点距離だけ離れた位置にビームスポットを形成します。このビームスポットからの光は均一で、光源像は形成しません。
最終更新日:2021年5月7日
移動ステージに取付けられたコンポーネントを、アジャスタを介して伝わる振動から絶縁できるか?
移動ステージは、アジャスタからの振動を下部(ベース)プレートに結合させることで、可動部である上部プレートには影響しにくいように設計することができます。アジャスタを固定するバレルクランプをベースプレートに取り付けることにより、アジャスタの操作時にステージに取り付けられたオプトメカニクス部品が受ける振動を最小に抑えることができます。

Click to Enlarge
図2:上の写真ではアジャスターネジを取り外しているため、上部プレートがバレルクランプから独立していることがより分かりやすくなっています。上部プレートは手前側の位置に戻っており、下部プレートに取り付けられているバレルクランプのベースよりも高い位置にあります。

Click to Enlarge
図1:直線移動ステージMT1B(/M)のバレルクランプが見えます。クランプは下部プレートに取り付けられているため、上部プレートはアジャスターネジに触れたときの振動から絶縁されています。
ステージとアジャスタの接触について
移動ステージには、バレルクランプによって手動アジャスタや電動アクチュエータが取付けられています(図1)。アジャスタのバレルはクランプによってしっかり固定されており、アジャスタからクランプへの振動を効率的に結合する強固な機械的接触になっています。クランプは直接下部プレートにボルトで固定されているため(図2)、アジャスタに触れることによる振動はステージの固定部に伝わります。この振動は光学テーブルまたはステージが固定されている取付け面によって減衰します。
アクチュエータとオプトメカニクス部品が取り付けられている上部プレートが直接接触するのは、アクチュエータ先端の1点のみです。この接触は強固な接続ではないため、アクチュエータと上部プレート間の振動の結合は弱くなります。同様に、上部プレートと下部プレートの接触点も強固ではないため、振動は効率的には伝わりません。
移動ステージに関するその他の情報
こちらからは、ステージの取付け方法や手動アジャスターネジを電動アクチュエータに交換する方法など、移動ステージに関するその他の情報を動画でご覧いただけます。
最終更新日:2020年9月2日
ポストホルダ: 穴の内側の長方形の溝について
Click to Enlarge
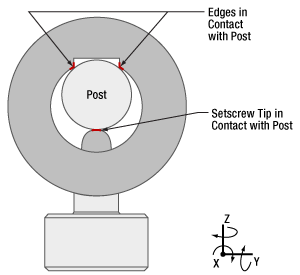
図4:上から見た図。ポストとポストホルダの間の3つの接触点(赤で表示)で、ポストのYZ軸に対する移動や回転を止めています。X軸に対する移動や回転は摩擦力で抑止されます。

Click to Enlarge
図 3:当社のポストホルダの穴の内側には鋭いエッジの溝が加工されています。

図 5:ブローチには上図のように刃が並んでおり、その高さは徐々に高くなっています。刃を材料に接触させ、機械でブローチを表面の端から端まで引っ張ります。各刃はそれぞれ少量の材料を削りとり、ブローチ加工された溝の深さは刃全体の高さの差と同じになります。
当社の全てのポストホルダには、穴の内側に沿って平行なエッジを有する溝が作られています(図3)。止めネジ(セットスクリュ)を締め付けることで、ポストが溝の2つのエッジに押し付けられます(図4)。エッジ間の距離が広いため(ポストホルダ内径の約半分)、ポストはエッジに対して安定に保持され、また再現性も得られます。
溝の2つのエッジに接触することでY軸とZ軸に対する移動と回転が止められるため、ポストの6つの自由度のうちの4つが拘束されます。また、ポスト側面と溝のエッジ間の摩擦により、残りの2つの自由度であるX軸に対する移動と回転が抑止されます。
穴の内側に溝が無い場合には、ポストとポストホルダの接触は1本の線になります。ポストにはZ軸回りの回転とY軸に沿った移動の自由度が残り、その位置は安定しません。
この不安定さによる光学セットアップ内の各部品位置のシフト量がサブマイクロメートルのレベルであったとしても、累積することでシステムの性能に重大な悪影響を及ぼす場合があります。また、システムを頻繁に再アライメントする必要が生じるかもしれません。
ブローチ加工
ポストを安定に保持するためには、溝のエッジは直線状でなければならず、隆起や凹凸があってはなりません。これらのポストホルダの溝は、ミクロンスケールで見ても直線状の鋭いエッジを有しています。エッジの直線性が不完全な場合には、ポストがホルダ内で動いたり、ホルダ内でのポストの位置再現性が得られなくなったりする場合があります。
溝の滑らかで直線状のエッジは、ブローチ加工と呼ばれる機械加工によって作ることができます。ブローチ(図5)は鋸に似ていますが、その刃の高さは徐々に高くなっています。
表面に沿ってブローチを引っ張ると、各刃はそれぞれ少量の材料を削り取ります。ブローチによって切削される溝の深さは、刃全体の高さの差(H2 - H1)に等しくなります。
溝を作るうえでブローチ加工が他の加工方法に比べて好まれる理由は、直線状の加工が可能であるほかに大量生産にも対応できるためです。
最終更新日:2019年12月11日
1
ベースは、アンダーカットのある面を下向きに置くと安定します
Click to Enlarge
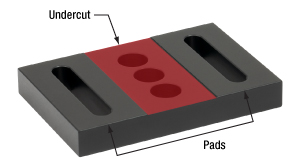
図7この図はベースの下側を示しており、赤く表示された箇所がアンダーカットです。この部分を切除することで、極めて平坦なパッドを実現できます。

Click to Enlarge
図 6:適切な安定性を得るため、ベースはアンダーカットがある面を光学テーブルまたはブレッドボードに向けて取り付けてください。

Click to Enlarge
図9:当社のデバイスに付いているパッドは、ボルトで固定したときに安定性が向上します。パッドは非常に平坦で、アンダーカット(赤で表示)から突き出た形になっています。アンダーカットによりテーブルやブレッドボードとの接触面積が制限されます。

Click to Enlarge
図 8:ステージやその他のデバイスの取付けプラットフォームにはパッドがありません。
アンダーカットはBA2/Mのようなベースの下側の面に機械加工されます(図6と7)。アンダーカットによりパッドと呼ばれる脚ができます。最大限の安定性を得るため、パッドがテーブルやブレッドボードに接触するようにベースを置いてください。
ベースの上側の面にはアンダーカットは無く、部品取付け用の面になっています。
ベースを上下逆に取り付けると、ベースがテーブルやブレッドボード上で動いたり、その他の機械的な不安定性が生じたりする場合があります。
パッドの平面度
パッドの平面度を向上させる鍵はアンダーカットです。パッドは、アンダーカットの加工後に平面加工されます。
この工程で生じる摩擦熱でパッドが加熱され、平面度はそれによって影響をうけます。アンダーカットでパッドの表面積を小さくすることで、この工程での発熱量が抑えられます。
機械加工においては、発生する熱を最小限に留めることは有益です。金属は加熱されると膨張しますが、機械加工中に発生する不均一な加熱により、部品の寸法が歪む場合があります。加工中に部品の寸法が歪むと、冷却後の部品には高いスポットやその他の望ましくない形状が残る可能性があります。そのような部品を使用すると、不安定性やミスアライメントにつながる場合があります。
精密な機器やデバイスのパッド
パッドの付いたほかの例として、図8と9に直線移動ステージLX10(/M)を示します。
最終更新日:2019年12月9日
2
Insights:光ファイバ
スクロールするか下のリンクをクリックすると、光ファイバを使用するセットアップを設計する際に考慮すべき点がご覧いただけます。
- NAはファイバの受光角を表す指標となり得るか
- MFDがシングルモードファイバにおいて重要な結合パラメータである理由とは
- NAによりシングルモードファイバからのビーム広がり角がわかるか
- シングルモードファイバへの光の結合効率に影響する因子は?
- 最大受光角はマルチモードファイバのコア全体に渡り一定か
NAはファイバの受光角を表す指標となり得るか
Click to Enlarge
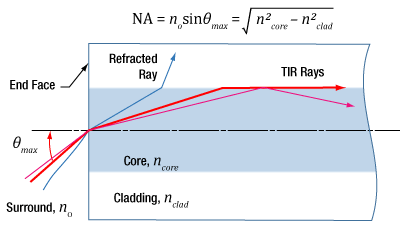
図1:入射角が≤θmaxの光線は、コアとクラッドの界面で全反射(TIR)するため、マルチモードファイバのコア内に閉じ込められます。全反射する条件は、ncore > nclad です。
Click to Enlarge
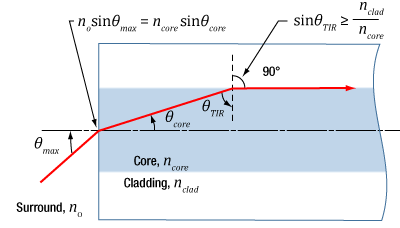
図2:コアとクラッドの境界での光の作用は、コアとクラッドの屈折率に依存し、端面に入射された光がコア内に結合するかを決定します。NAは幾何学的計算と、図の上にある2つの式を用いて求められます。
開口数(NA)は、ほとんどのマルチモードファイバにおいて図1のように最大の受光角を表します。この関係性はシングルモードファイバにおいては適用することができません。
受光角とNA
光線モデルでは、光線がファイバのコアに結合するか否かは入射角によって決まります。カットオフ角は最大受光角(θmax )で、NAに関連します(図1)。
入射角が≤θmaxの光線は、ファイバのコアとクラッド間の境界において全反射(TIR)します。これらの光線はファイバ内を伝搬していくので、コア内に閉じ込められたままとなります。
入射角がθmaxよりも大きい光線については、コアとクラッド間の境界で屈折し、部分的に透過する成分が生じます。この光はしばらくの間クラッド内を伝搬する場合がありますが、最終的にはファイバから損失していきます。
関係性は幾何学によって定義されます
NAとθmaxの関係性が図2で示されています。両界面にはスネルの法則が用いられ、sin(90°) = 1が代入されています。この図では、コアとクラッド間の境界で全反射が生じる最も極端な条件を示しています。
コアncore とクラッドnclad の屈折率が重要な役割を果たします。全反射が起きるにはncoreがnclad よりも大きくなければなりません。その差が大きければ大きいほど、NAと最大受光角も大きくなります。
入射角とファイバのモード
入射角が≤θmax のとき、入射光はマルチモードファイバの導波モードのどれか1つに結合されます。一般的に言えば、入射角が小さければ小さいほど、励起されるファイバのモード次数も小さくなります。次数が小さいモードは、強度をコアの中心近くに集中させます。次数が最も小さいモードは、端面に垂直に入射された光によって励起されます。
シングルモードファイバではご利用いただけません
シングルモードファイバの場合、図2のような光線モデルは使用できず、計算した開口数(受光角)は、最大の入射角度に等しくはなく、またファイバの集光能力を表すものではありません。
シングルモードファイバの導波モードは1つ、次数が最も小さいモードで、入射角が0°の光によって励起されます。しかし、NAを計算すると、その値は0ではありません。光線モデルでは、シングルモードファイバから放射、または結合される光線の広がり角を正確に予測することもできません。ビームの広がりは回折効果によって起こりますが、光線モデルにおいては考慮されていません。しかし、波動光学モデルによれば説明可能です。ガウシアンビームの伝搬モデルを使用すれば高確度でビームの広がり角を求めることができます。
最終更新日:2020年1月20日
1
MFDがシングルモードファイバにおいて重要な結合パラメータである理由とは
Click to Enlarge
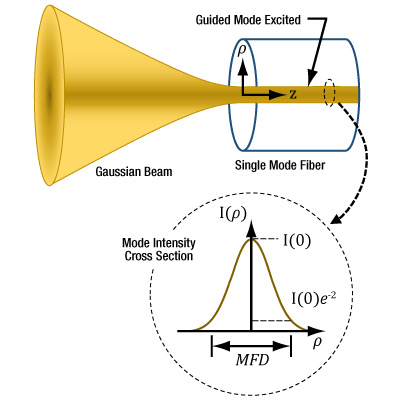
図3:最大の結合効率でシングルモードファイバに結合するためには、光が軸上のガウシアンビームで、ウェスト位置がファイバの端面にあり、ウェスト径がMFDと等しくなる必要があります。ファイバの出射光もこれらの特性によりガウス分布に近い形状となります。シングルモードファイバにおいて、開口数(NA)の使用した光線モデルは、結合状態を決定するには不適切です。ここでは半径( ρ )におけるモード強度(I )プロファイルが示されています。
光はシングルモードファイバを伝搬していくと、そのビーム断面の強度分布はガウス分布に似た形状となります。モードフィールド径(MFD)はこの強度プロファイルの幅を表します。入射ビームがこの強度プロファイルに合致すればするほど、より効率よく多くの光がファイバに結合します。入射されるガウシアンビームのビームウェストがMFDと等しいと、とりわけ高い結合効率が得られます。
ガウシアンビームの伝搬モデルにおいてMFDをビームウェストにすることで、確度の高い入射ビームパラメータと出射ビームの広がり角を得ることができます。
結合条件の決定
光ファイバの利点は、ファイバの導波モードによって伝播される光が放射線状には広がらず、最小限の減衰で伝搬していくことです。光をファイバの導波モードに結合するには、入射ビームと導波モードの特性を一致させる必要があります。導波モードに結合しない光はファイバの外に放射されます。光がファイバから漏れ出したと言えるのです。
シングルモードファイバの導波モードは1つであり、波動光学解析によってモードをベッセル関数で表すことができます。ガウス関数とベッセル関数の振幅プロファイルは、非常によく似ており[1]、代わりにガウス関数を使用すると正確な結果をもたらしながら、ファイバのモードのモデリングが簡易化されるので便利です。
図3では、入射光が導波モードに結合するために一致しなければならないシングルモードファイバの断面方向の強度分布を示しています。強度(I )プロファイルは、径方向距離( ρ )のガウス関数にほぼ一致します。MFDは、ファイバ長に沿って一定で、e-2とピーク強度の積に等しい強度の幅です。モードフィールド径(MFD)内は、ビームパワーの約86%が含まれます。
次数が最も小さい横モードだけが放射されるレーザ出力光はガウシアンビームとなるため、このレーザ光はシングルモードファイバに良い結合効率で結合できます。
シングルモードファイバへの光の結合
シングルモードファイバのコアに効率よく光を結合するには、入射するガウシアンビームのウェストをファイバの端面に合せてください。ビームウェストの強度プロファイルは、モードの断面の強度の特性と重複し、合致しなければなりません。入射ビームに必要なパラメータは、ガウシアンビームの伝搬モデルとファイバのMFDから求めることができます。
結合効率が小さくなるのは、ビームウェスト径とMFDが一致しない、端面のモーダルスポットによりビームの断面のプロファイルが歪んだり、中心がずれている、光がファイバの軸に沿って誘導されていない場合に起こります。
参考文献
[1] Andrew M. Kowalevicz Jr. and Frank Bucholtz, Beam Divergence from an SMF-28 Optical Fiber (NRL/MR/5650--06-8996) (Naval Research Laboratory, Washington, DC, 2006).
最終更新日:2020年2月28日
2
NAによりシングルモードファイバからのビーム広がり角がわかるか
開口数(NA)を使用してシングルモードファイバから出射される、あるいはシングルモードファイバに結合する光円錐を概算する場合、大きな誤差が生じる場合があります。広がり角はガウシアンビーム伝搬モデルを使用した方がより良い概算値が得られます。このモデルにより、広がり角を算出し、用途に適したビームスポットサイズを得ることができます。
シングルモードファイバにおけるモードフィールド径(MFD)内は、ビームパワーの約86%が含まれるため、MFDによりスポットサイズを決めることは、シングルモードファイバから光をコリメートしたり、光を集光する際の適切な定義であるとされています。一次近似でファーフィールドで測定されたとき、
 , , | (1) |
は、広がり角または受光角(θSM )(単位:ラジアン)です。これは1/2ビーム角で、波長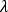 )
)
| Rayleigh Range: | ||
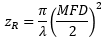 | ||
| Beam Radius at Distance z: | ||
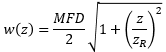 | ||
図 4:青い線は、シングルモードファイバからの出射光の広がり角(θSM )をNAを用いて計算した結果を示しています。赤い線は、ガウシアンビーム伝搬モデルを使用して計算されており、これにより、ビームスポット径の大きな誤差を回避することができます。 こちらのグラフではSM980-5.8-125からのビームをモデル化しています。NAは0.13、MFDは6.4 µmの値を使用しています。動作波長は980 nm、レイリー範囲は32.8 µmでした。 | ||
ガウシアンビームによるアプローチ
シングルモードファイバの端面から出射される光は円錐状に広がりますが、この光はファイバ軸から様々な角度で出力する複数の光線と同様の振る舞いにはなりません。
この光はガウシアンビームに似ており、モデル化ができます。放射光がガウシアンビームと同様に伝搬するのは、光の導波モードがガウス分布に近似しているからです。
ガウシアンビームの広がり角は、光線として作用する光を想定して計算された広がり角度とは実質的に異なります。光線モデルを使用した場合、広がり角は sin-1(NA)となります。しかし、NAと広がり角の関係性は高次マルチモードファイバのみ有効です。
図4では、NAを使用して広がり角を計算すると大きな違いが生じる可能性を示しています。 ガウシアンビームでは、広がり角はビームパワーの86%を含む領域とされており、この領域の境界円における強度は、ピーク強度の1/e2となっています。
図4の右の式は、シングルモードファイバ端面から出射されるビームの広がり角を正確にモデル化するガウシアンビームの式です。計算に使用するファイバのMFD、NAならびに動作波長を含む値はグラフ下に記載されています。ビーム発散角は、1/e2半径によって定義されたビームサイズの変化により算出されています。ビームサイズは、z < zRの距離においては非線形で、ファーフィールド(z >> zR)においてはほぼ線形に変化します。
グラフに記載されている角度は各曲線の傾斜から計算されました。式(1)で求めたファーフィールドの概算が使用された場合、広がり角は0.098ラジアン(5.61°)です。
参考文献
[1] Andrew M. Kowalevicz Jr. and Frank Bucholtz, Beam Divergence from an SMF-28 Optical Fiber (NRL/MR/5650--06-8996) (Naval Research Laboratory, Washington, DC, 2006).
最終更新日:2020年2月28日
Content improved by our readers!
3
シングルモードファイバへの光の結合効率に影響する因子は?
Click to Enlarge
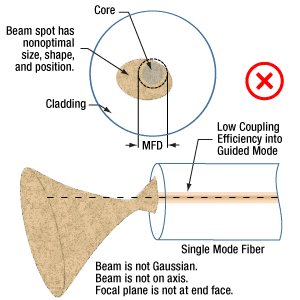
図6:シングルモードファイバへの光の結合効率を低下させる条件とは、入射ビームと、ファイバ導波モードの光学特性の類似性を損なわせるあらゆる状態です。
Click to Enlarge
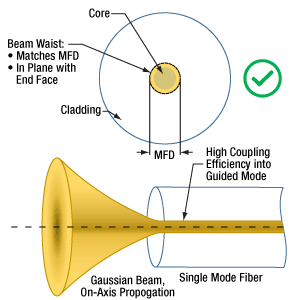
図5:最大の結合効率でシングルモードファイバに結合するためには、光は軸上のガウシアンビームで、ウェスト位置がファイバの端面にあり、ウェスト径がMFDと等しくなる必要があります。
入射ビームの角度、位置、強度プロファイルの調整により、シングルモードファイバへの光の結合効率を向上させることができます。ファイバの端面が平坦かつファイバの長軸方向に対して垂直であることを想定し、結合効率は下記の基準を満たすビームにおいて最適化されます(図5参照)。
- ガウス分布の強度プロファイル
- ファイバ端面に垂直入射
- ビームウェストがファイバ端面にある
- ビームウェストの中心位置がファイバのコアにある
- ビームウェスト径がファイバのモードフィールド径(MFD)と等しい
これらの理想的な結合条件からかけ離れた状態を図6で示しています。
これらのビーム特性は、シングルモードファイバの導波モード [1]の波動光学論に従っています。
光源による結合効率の制限
次数が最も低い横モードを放射するレーザのみがガウス分布に近似するビームを生成し、そして結合効率の良い光をシングルモードファイバに結合することができます。
マルチモードファイバーレーザまたは広帯域光源からシングルモードファイバの導波モードに結合された光は、光がファイバ端面のコア領域に集光されたとしても結合効率は低くなります。 これらの光源からの光の大部分は、ファイバから漏れ出します。
結合効率が低い要因は、これらのマルチモード光源の光の一部のみしかシングルモードファイバの導波モードの特性に合致しないからです。光源の光を空間的にフィルタリングすることで、ファイバのコアに結合される光の量を見積もることはできます。シングルモードファイバが受光できるのは、最大でもフィルタを通ったガウシアンビームの光のみとなります。
マルチモード光源の光のファイバーコアへの結合効率は、シングルモードファイバの代わりにマルチモードファイバを使用すると改善します。
参考文献
[1] Andrew M. Kowalevicz Jr. and Frank Bucholtz, Beam Divergence from an SMF-28 Optical Fiber (NRL/MR/5650--06-8996) (Naval Research Laboratory, Washington, DC, 2006).
最終更新日:2020年1月17日
4
最大受光角はマルチモードファイバのコア全体に渡り一定か
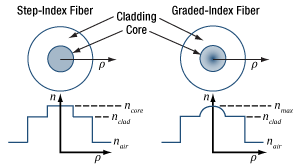
これはファイバの種類によって異なります。ステップインデックスマルチモードファイバは、ファイバのコアのどの位置においても最大受光角は同じです。反対にグレーデッドインデックスマルチモードファイバは、コアの中心部のみで、入射角が最大範囲である光線を受光します。最大受光角は、中心から離れるにつれ小さくなり、クラッドの境界近くでは0°に近くなります。
Click to Enlarge
図7: ステップインデックスマルチモードファイバの屈折率( n )は、コア全体に渡り一定です。グレーデッドインデックスマルチモードファイバの屈折率はコアに渡り変動します。最大の屈折率は通常、コアの中心です。
Click to Enlarge
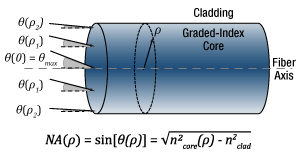
図 9:グレーデッドインデックスマルチモードファイバの受光角は半径( ρ )によって異なります。なぜならコアの屈折率が径方向の距離によって変動するからです。通常、最大受光角は中心付近、0°に近い最小受光角はクラッドの境界付近で起こります
Click to Enlarge
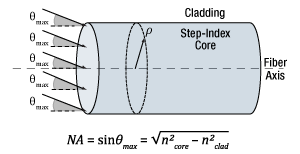
図 8:ステップインデックスマルチモードファイバは、角度が≤|θmax |の入射光を良好な結合効率でコアに受光します。最大受光角はコア半径( ρ )に渡り一定です。ファイバ端が空気に接していることを想定しています。
ステップインデックスマルチモードファイバ
ステップインデックスマルチモードファイバのコアは、図7の左上に示すようなフラットトップの屈折率プロファイルを有します。 光がファイバの平坦な端面に入射されたとき、最大受光角(θmax )は、コアのどの位置においても同じです(図8)。これはコア全体にわたって屈折率が一定であり、そして受光角はクラッドの屈折率に大きく依存するからです。
光が入射されるのがコアの中心だろうと端だろうと、ステップインデックスマルチモードファイバは、ファイバの軸に対して±θmaxの角度内の光円錐を受光します。
グレーデッドインデックスマルチモードファイバ
図7の右上に示すような一般的なグレーデッドインデックスマルチモードファイバは、屈折率がコアの中心で最も高く、径方向の距離( ρ )に反比例して小さくなります。図9の式は、径方向距離の依存したコア屈折率により、最大受光角、すなわち開口数(NA)が算出できることを示しています。この式は、ファイバ端面が、平坦で、空気と接しており、ファイバ軸に対して垂直であることを想定しています。
図9では、コアの屈折率により角度が制限されている光錐を示しています。最大の角度の広がり
ステップインデックスか、グレーデッドインデックスか?
ステップインデックスマルチモードファイバの方がグレーデットインデックスマルチモードファイバよりもより多くの光を集める可能性があります。これは、ステップインデックスのコアに渡り、開口数(NA)は一定で、グレーデッドインデックスのコアでは放射距離に応じてNAが小さくなるからです。
しかし、グレーデッドインデックスのプロファイルにより、すべての導波モードで同じような伝搬速度が得られるため、ビームがファイバを伝送する際のモード分散が小さくなります。
できるだけ多くの量の光をマルチモードファイバに結合する必要がある用途で、モード分散に敏感ではない場合には、ステップインデックスマルチモードファイバの方がより良い選択となります。逆のケースにおいてはグレーデッドインデックスマルチモードファイバを検討する必要があります。
参考文献
[1] Gerd Keiser, Optical Fiber Communications (McGraw-Hill, New York, 1991), Section 2.6.
最終更新日:2019年1月2日
5
コンデンサの開口数(NA)は、顕微鏡の分解能に影響を与えるか
コンデンサの開口数(NA)は、顕微鏡の分解能に大きな影響を与えます。その理由は、試料への光の入射角の範囲が、試料を透過する、あるいは試料で反射される光の角度範囲に影響を与えるためです。分解能を最適化するための一般的な方法は、少なくとも対物レンズのNAと同等以上のNAを有するコンデンサを使用することです。言い換えると、コンデンサによって形成される光の円錐の頂角は、対物レンズが受光する角度範囲と一致するか、またはそれ以上でなければなりません。
Click to Enlarge
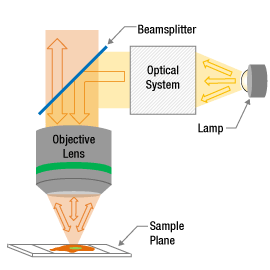
図2:落射照明顕微鏡では、対物レンズから光が試料に照射されます。対物レンズは試料からの反射光や散乱光を集光する役割も果たします。そのため、図1とは異なり、照射の角度とイメージングの角度はどちらも対物レンズのみに依存します。
Click to Enlarge
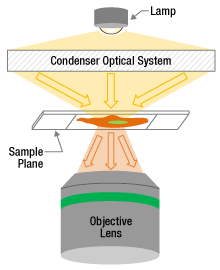
図 1:透過型顕微鏡では、光源からの光はコンデンサ光学系を通して試料に照射されます。その透過光は対物レンズによって集光されます。集光された光から、カメラあるいは接眼レンズを用いて像が生成されます。
Click to Enlarge
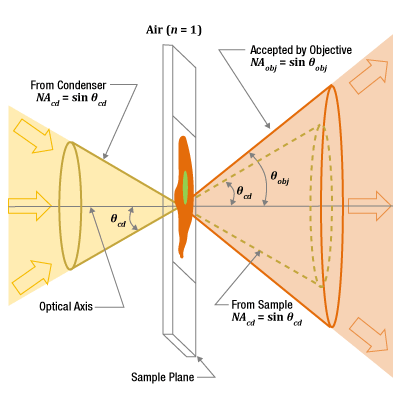
図3:コンデンサから試料上の1点に入射する光(左、薄黄色)、試料を透過する光(右、点線)、および対物レンズが集光可能な光の範囲(右、オレンジ色)を示す円錐。円錐の角度は光軸からの角度です。試料に入射する光の円錐の半頂角と試料を透過する光の円錐の半頂角がほぼ同じ
コンデンサと対物レンズ
透過型顕微鏡では、コンデンサは光源からの光を集光して試料に照射します(図1)。コンデンサ光学系には通常いくつかの光学素子が含まれ、アライメントすることで試料面を均一に照明することができます。対物レンズは試料面の反対側に位置し、試料を透過した光を集光します。この集光された光から、接眼レンズあるいはカメラを用いて像が生成されます。
これに代わって、対物レンズが試料への光の照射と試料からの光の集光の役割を共に果たすように、顕微鏡を構成することもできます(図2)。この場合には独立したコンデンサ光学系はありません。
開口数(NA)
コンデンサは試料面に対して光を様々な角度から照射します(図3)。試料上の1点を頂点とし、コンデンサからの光の円を底面とする円錐を用いて、光の入射角範囲(θcd )を定量化することができます。試料上の点を透過した光の角度範囲は、入射した光の角度範囲とほぼ同じです。対物レンズが集光できる角度範囲(θobj )は、それとは異なる円錐を用いて示すことができます。
これらの角度範囲は、次のレンズの開口数(NA)の式を用いて定量化することができます。
NA = n sin(θ ),
NAは円錐の半頂角(θ )と、周囲の媒質の屈折率(n )に依存します。NAが大きいほど、角度範囲を示す円錐は広がります。 この角度は光軸からの角度です。
例えば、対物レンズのNAが0.7で、レンズと試料の間が空気(
分解能
顕微鏡の分解能(δ )、「どれくらいまで近接した2点を分離してイメージングできるか」という性能を表します。この最小距離を見積るときに、一般的に
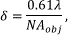
という式が用いられますが、ここには波長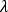 )
)
NAcd ≤ NAobj の場合には、修正された式、
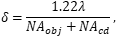
を用いることでより良い近似値が得られます。またこの式はコンデンサのNAが分解能にとって重要であることを示しています。
最終更新日:2021年6月9日
顕微鏡におけるケーラー照明について
Click to Enlarge
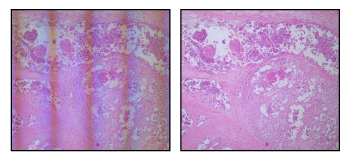
図4:光源の像として発光素子の構造が見えます(左)。ケーラー照明では、光源の像が試料面やカメラセンサ面に形成されず、試料面の照明は均一になります(右)。
複数の要素で構成される顕微鏡システムでは、ケーラー照明になるように調整することができます。ケーラー照明では、ランプやLEDのような光源から集光される光と、試料から集光される光とで像の結び方が異なります。光源からの光は、試料(物体)面やカメラのセンサ面に結像させないようにします。試料面の照明では、一般に幅広い角度から均一に光が当たるようにしますが、これは高分解能イメージングを行う上では必要とされます。その結果、ケーラー照明ではランプやLED光源の像がカメラセンサ上で重畳(スーパーインポーズ)されないことになります。
光源の像
光源からの光が試料面に結像すると、均一な光が試料に当たらないことになります(例:図4左)。この画像では発光体の構造がはっきりと見えています。これに対してケーラー照明では、光を平行光線束にして試料面に照射するため、試料面での照明は均一になります(図4右)。また、光学系を調整してケーラー照明とすることで、カメラセンサ上に光源が結像することも防止できます。それにより、光源の発光体の構造が試料の画像に重畳されることは無くなります。
照明光路
照明光路は、光源から始まり、試料を通ってカメラセンサに到達します。下の動画(動画1)では、ランプまたはLEDなどの分散光源からの光線を追跡しています。
光源上の複数の放射ポイントから、光は様々な角度で放射されます。その光は集光レンズで集光され、さらに伝播する光は視野絞りによってその最大径が制限されます。次に光は視野レンズを通過し、それにより開口絞りの位置で光源の各ポイントの像が形成されます。開口絞りはコンデンサーレンズの前側焦点面に配置されるため、開口絞りでの光源の像のアライメントは重要です。
開口絞りにおける光源の像からの光は、コンデンサーレンズによって平行光線束に変換されます。各光線束は光源の像の個々の点から始まります。特定の光線束が試料面に入射する角度は、その光源上の点が光軸から離れているほど大きくなります。言い換えれば、開口絞りを絞ることで照明の角度範囲は狭くなり、試料面での照明強度も低下します。
光源の像の位置は、コンデンサーレンズの前側焦点面にあるため、試料面には平行光線束のみが入射します。試料面では光源の像は形成されず、照明は均一になります。
試料面を透過した光源からの光は、対物レンズの後側焦点面(対物レンズとチューブレンズの間)で結像します。光源の像はカメラセンサ上では形成されないため、像の品質は維持されます。
イメージング光路
イメージング光路は試料面から始まり、カメラセンサで終わります。動画ではこの光路の光線も追跡しています。試料上の各点からの光はカメラセンサ上の1点に結像します。
動画1:透過型顕微鏡における光学素子(左)は、ケーラー照明が得られるように調整された状態で表示されます。その条件下では、動画の照明光路を追跡した光線で示されるように、試料面は均一に照明され、光源の像が試料面やカメラセンサ上で重畳することはありません。一方、イメージング光路を追跡した光線は、同じ光学素子の配置で 試料面の像がカメラセンサ上に形成されることを示しています。
最終更新日:2021年6月18日
積分球によって放射されるUV蛍光ならびに青色蛍光
Click to Enlarge
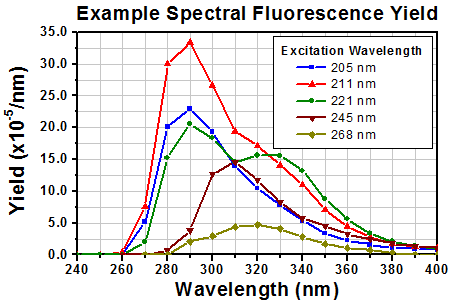
図1:各波長における典型的な蛍光収量は、励起波長の強度より4桁程度低くなっています。[4]
蛍光スペクトルの収量は、積分球内で発光する蛍光の強度と励起波長の強度により決まります。収量(Yield)は積分球の内面全体で励起した蛍光量(波長に依存)を励起光の強度で割って計算します。
データご提供:Dr. Ping-Shine Shaw, Physics Laboratory, National Institute of Standards and Technology, Gaithersburg, MD 20899, USA.
積分球内面のコーティングにはポリテトラフルオロエチレン(PTFE)が使用されています。この素材は白色ですが、幅広い波長において高い、かつ平坦な反射率と、化学的不活性があることなどの理由から好まれます。
しかし、積分球はPTFEならびにPTFEよりも反射率が低い硫酸バリウムでコーティングされており、UV光を照射した場合、低量ではありますがUVならびに青色の蛍光を発光することにご留意ください。[1-3]
PTFE内の炭化水素
蛍光発光しているのはPTFE自体ではなく、UVならびに青色の蛍光の原因はPTFE内の炭化水素です。コーティングの原料には低量の炭化水素不純物が存在しており、また積分球を使用したり保管している間に汚染源によりさらに炭化水素がコーティング材に付着します。[1]
蛍光波長域と強度
米国標準技術研究所(National Institute of Standards and Technology/NIST)の研究者がPTFEコーティング付き積分球の励起蛍光を調査しました。積分球の全蛍光量を蛍光波長と励起波長を変えて測定しています。最大蛍光量は、励起光強度より4桁程度低くなりました。
PTFEから発光するUVならびに青色の蛍光は主に200 nm~300 nmの吸収帯で励起されます。蛍光は図1のとおり250 nm~400 nmの波長範囲で発光します。励起波長を長波長側にすることにより、短い波長で発光する蛍光量が少なくなり、蛍光スペクトルの形状が変動することが示されています。
PTFE内の炭化水素のレベルが高くなると、蛍光量も多くなります。それに伴い、積分球からの出力量は吸収帯波長において少なくなります。それは、このスペクトル域においてより多くの光が吸収されるからです。[1, 3]
使用への影響
PTFEから発光するUVならびに青色蛍光は、多くの用途において影響はほとんどありません。蛍光の強度が小さく、励起されるのは主に300 nm未満の入射波長の場合だからです。この蛍光に影響される用途には、UV放射の長期に渡る測定、UV光源の校正、UV反射率標準の確立、UVリモートセンシングの実施などがあります。
蛍光の影響の最小化
蛍光レベルの最小化ならびに安定化のためには、積分球をガソリン・ディーゼルエンジンの排気や、ナフタレン・トルレンなどの溶剤を含めあらゆる炭化水素源から隔離することが必要です。また、炭化水素による汚染は最小化または減少することはできますが、完全に除去できないことにご留意ください。[1]
炭化水素に曝される履歴は積分球ごとに異なるため、個別の積分球における入射光への応答性を予測することはできません。蛍光により、用途への悪影響があった場合には、積分球の校正をお勧めいたします。下記[4]では、校正に必要な光源(対象の波長にわたってスペクトルがよく知られている重水素ランプやシンクロトロン放射)、モノクロメータ、ディテクタ、積分球と、その手順について説明しています。
参考文献
[1] Ping-Shine Shaw, Zhigang Li, Uwe Arp, and Keith R. Lykke, "Ultraviolet characterization of integrating spheres," Appl.Opt. 46, 5119-5128 (2007).
[2] Jan Valenta, "Photoluminescence of the integrating sphere walls, its influence on the absolute quantum yield measurements and correction methods," AIP Advances 8, 102123 (2018).
[3] Robert D. Saunders and William R. Ott, "Spectral irradiance measurements: effect of UV-produced fluorescence in integrating spheres," Appl. Opt. 15, 827-828 (1976).
[4] Ping-Shine Shaw, Uwe Arp, and Keith R. Lykke, "Measurement of the ultraviolet-induced fluorescence yield from integrating spheres," Metrologia 46, S191 - S196 (2009).
最終更新日:2020年1月22日
1
試料交換誤差について
Click to Enlarge
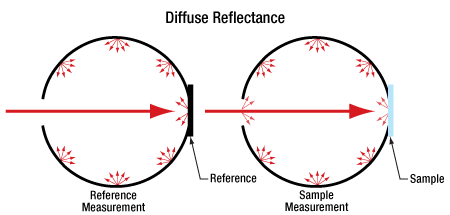
図 2:拡散試料の透過率と反射率を上記のように測定することによって、試料交換誤差に起因する試料スペクトル歪みがもたらされる可能性があります。問題は基準試料と測定したい試料測定時の、試料領域の反射率が異なることです。
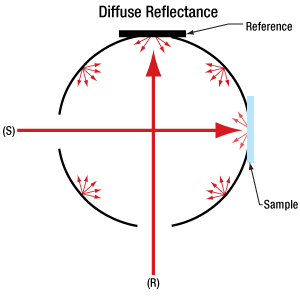
Click to Enlarge
図 3:上の実験構成では、積分球内の条件が基準試料測定時と測定したい試料測定時で同じのため、試料交換誤差の影響は受けません。基準試料測定時、光は(R)に沿って通り、(S)に沿っては通りません。反対に測定したい試料測定時、光は(S)に沿って通り、(R)に沿っては通りません。
積分球を使用することにより光学試料の透過ならびに拡散反射スペクトルの絶対値が測定できます。これらのスペクトルは、測定したい試料と基準とする試料の両方のスペクトルを測定することによって求められます。
基準試料の測定は、照射光源のスペクトルを知る上で必要です。基準試料のスキャンで得られた値により、測定したい試料の測定値から光源のスペクトル測定値を差し引くことができます。
光源の基準測定は、透過率データの場合、試料を配置せずに測定し、反射率測定の場合には高反射の基準試料を置き、測定します。
この試料測定や基準試料測定時において試料交換誤差が生じた場合、この誤差の影響がない実験手法でない限り、補正された試料スペクトルの確度に悪影響を及ぼす場合があります。
試料交換誤差をもたらす条件
積分球の光学性能は、内面の各位置での反射率に依存します。透過スペクトルや拡散反射スペクトル測定時、積分球の内面の一部分に試料を置きます(図2)。しかしそのような内面の一部が変化することにより、積分球の性能が変動します。
試料交換誤差は、測定手順の中で、積分球内の試料をほかの試料に交換することがあるときに懸念されます。例えば、拡散反射を測定しているとき(図2下)、最初の測定は基準試料を積分球内に取り付けて実施するとします。次にこの試料を取り外して測定したい試料に交換し、2回目の測定を行います。そして両方のデータセットを利用して、試料の補正拡散反射率(絶対値)を求めます。
この手順では、試料スペクトルに歪みが生じます。測定したい試料と基準試料の吸収ならびに散乱特性が異なるため、これらを交換することで積分球内の試料面部分の反射率が変わってきます。2つの測定において積分球の平均反射率が変わってくるため、基準試料と測定したい試料には完全な互換性がありません。
解決策1:測定したい試料と基準試料を同時に取付ける
試料交換時の誤差を回避する1つの実験手法は、測定したい試料と基準試料を同時に積分球内に取付け、測定データを取得することです。この手法では、2つの試料を追加ポートとして取り付けられる大きさの積分球が必要です。
光源は積分球の外側に配置し、測定したい試料と基準試料の両方を順次測定します。試料からの正反射、あるいは透過ビームは、積分球の外に誘導されているため、拡散光のみが検知されます。積分球の内面(の条件)は、どちらの測定でも同じのため、試料交換時の誤差の懸念はありません。
解決策2:試料用ポートならびに基準ポートから測定する
測定したい試料と基準試料が積分球内に同時に取付けられない場合、試料の交換が発生します。交換が必要な場合には、下記[1]で説明する手順で試料交換時の誤差を取り除くことができます。
この手順では合計で4回の測定が必要です。基準試料を設置時、2つの異なるポートから測定を行います。1回目の測定では基準試料が視野内にある方向から測定し、2回目の測定では試料が視野内に無い方向から測定します。その後測定したい試料に交換し、同様の測定を繰り返します。これらの測定値を利用して下記[1]に説明する計算をすることにより、試料交換時の誤差は取り除かれます。
参考文献
[1] Luka Vidovic and Boris Majaron, "Elimination of single-beam substitution error in diffuse reflectance measurements using an integrating sphere," J. Biomed.Opt. 19, 027006 (2014).
最終更新日:2019年12月4日
2
Insights:レーザ
スクロールするか下のリンクをクリックして動作レーザや取り付けるときのヒントについてご覧ください。
- レーザ装置からは、いつでもその筐体の軸に平行なコリメート光が放射されるか?
- 量子カスケードレーザ(QCL)とインターバンドカスケードレーザ(ICL):動作限界と発熱によるロールオーバ
- HeNeレーザ:取扱い方と取付け方のガイドライン
- チョッパーホイールを使用したビームサイズの測定法
- レーザ光に薄レンズの公式を適用できるか
レーザ装置からは、いつでもその筐体の軸に平行なコリメート光が放射されるか?
レーザは、レーザーパッケージの長軸に対して平行なビームを放射しない場合があります。この角度偏差はポインティング角度(θp)と呼ばれており、動画1で説明しています。角度偏差は、レーザの配置にピッチ(チップ)とヨー(ティルト)調整付きのキネマティックマウントを使用すると、補償することができます。
動画1:ポインティング角度(θp)は、コリメートされたレーザ光(赤い矢印)の方向と、レーザ筐体(点線)の長軸との間の角度偏差です。この軸はコリメータまたはコリメートされたレーザーパッケージの前面に対して垂直です。
動画2:コリメートレーザーパッケージPL202にアダプタAD11NTを取り付けることにより、ピッチ(チップ)とヨー(ティルト)調整を可能にするマウントKM100にレーザを固定するこができます。
角度偏差
ビームの角度偏差は、レーザがマウントに適切に取り付けられていない、レーザ共振器が筐体内の中央に完全に配置されていない、あるいはレーザーパッケージ内蔵の光学素子を透過するビームが偏向しているなど、いくつかの要素によって生じる場合があります。複合的な公差(公差の積み上げ)は非ゼロのポインティング角度をもたらします。
レーザが円筒形の筐体に納められている場合、この偏差はレーザをV溝付きマウントに置いて測定することができます。レーザを長軸周りに回転させ、レーザースポットの軌跡の円の直径を記録するのです。コリメートレーザーパッケージの仕様にはよく最大角度偏差が示されています。
角度補正にキネマティックマウントを使用
レーザ光の角度を補正する方法の1つに、キネマティックマウントをレーザを固定して、マウントのアジャスタを使用してレーザのピッチとヨーを調整する方法があります。
キネマティックマウントがレーザ筐体の外径に直接取り付け可能な場合があります。 キネマティックV字型マウントは、Ø38 mm(Ø1.5インチ)ポスト用V字型クランプも含め、アダプタを使用せずに様々な径の筐体に対応できるよう構成可能です。
そのほかのキネマティックマウントは径が固定の内孔です。レーザの筐体とマウントの内孔に対応するアダプタは、円筒形やSMネジ付き部品用など様々な種類をご用意しております。
アダプタの取り付け
アダプタAD11NTを使用してコリメートレーザーパッケージPL202をキネマティックマウントKM100に取付ける方法が動画2でご覧いただけます。アダプタを取り付ける前に、レーザーヘッドをキネマティックマウントの内孔の後ろから通してください。
マウントの内孔の背面にはストッパが付いているので、アダプタをアジャスタ側ではないマウントの面に取り付ける必要があります。ストッパはØ25 mm~Ø25.4 mm(Ø1インチ)光学素子を内孔に固定するのに役立ちますが、Ø25.4 mm(Ø1インチ)アダプタをマウント内孔の後ろ側から取り付けるのを防ぐ役割もあります。
アダプタにはレーザを固定するナイロンチップ付きの止めネジ(セットスクリュ)が付いており、またマウントにもアダプタを固定するナイロンチップ付き止めネジが付いています。ナイロンチップ付き止めネジを採用しているのは、表面に傷を付け、摩耗させないよう取り付けた部品をしっかり保持するためです。
そのほかにもポインティング角度の補正に関する情報が
こちらの動画ページでご覧いただけます。
最終更新日:2020年10月12日
量子カスケードレーザ(QCL)とインターバンドカスケードレーザ(ICL):動作限界と発熱によるロールオーバ
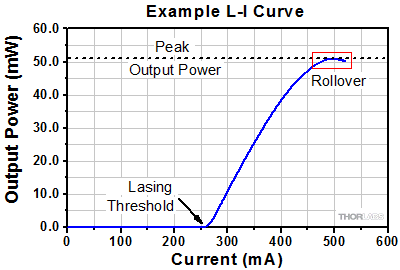
Click to Enlarge
図1:QCLのL-I(光出力-駆動電流)曲線例。QCLとICLレーザで典型的な非線形の勾配と、ロールオーバーの領域が見られます。動作パラメータがレーザ発振領域から発生する熱負荷を決定し、それがピーク出力に影響します。こちらのレーザは25 °Cに温度制御されたマウントに取り付けられています。
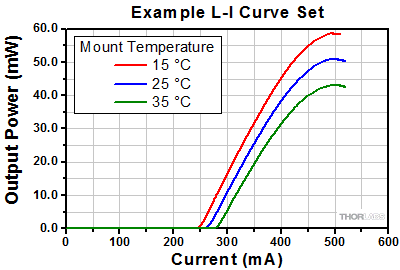
Click to Enlarge
図2:これらのQCLのL-I曲線は、マウント温度がピーク動作電流値に影響をおよぼすことを示していますが、一方で温度制御マウントを使用しても、ロールオーバ値を超え、レーザを損傷しかねない駆動電流が印加される可能性を排除できないことを示しています。
量子カスケードレーザ(QCL)とインターバンドカスケードレーザ(ICL)で測定された光出力-駆動電流特性(L-I)曲線には、図1の赤枠部分に示すロールオーバの領域があります。
ロールオーバの領域にはレーザのピーク出力が含まれます。こちらの例の駆動電流はちょうど500 mAの部分にあたります。この値より高い駆動電流は、レーザを損傷する危険性があります。
レーザ動作
これらのレーザでは、半導体層構造の設計によりエネルギー準位が制御されており、電子が励起準位から制御された準位に落ちる際のエネルギー差により発光します。これらの電子は駆動電流により供給されます。
電子がレーザのエネルギの準位を降りるとき、電子は光子の形でエネルギを放出しますが、電子は光子を放出する代わりに半導体素材に熱を与えることによってもエネルギを放出します。
熱の蓄積
レーザでは、電子の準位間遷移によるエネルギを100%の効率で光子に変換することはできません。エネルギを熱として放出する電子も存在し、それにより、レーザの発振領域の温度が上がります。
レーザ発振領域の熱は、逆に電子によって吸収される場合もあります。このように余分なエネルギが加わることにより、電子がしかるべきエネルギ準位に落ちずに散乱してしまう場合があります。その後、散乱した電子は通常エネルギを光子ではなく、熱として放出します。
レーザの発振領域の温度が上がるにつれ、電子はさらに散乱し、熱ではなく光を生成する電子の割合は小さくなります。温度の上昇はまた、レーザのエネルギ準位にも変化を及ぼし、結果、電子が光子を生成しにくくする場合もあります。これらがともに作用し、レーザ発振領域の温度が上昇し、レーザが電流をレーザ光に変換する効率が低下します。
動作リミットは熱負荷によって決定
L-I曲線の理想的な勾配は、閾値電流以上では線形になることです。図1においてこの閾値電流は270 mAのあたりです。しかし、駆動電流が増加すると勾配が小さくなります。これはレーザ発振領域の温度上昇の影響です。ロールオーバは、レーザが追加した電流をレーザ光に変換できなくなったときに起こります。追加した駆動電流は代わりに熱のみを発生させます。電流値が高くなりすぎると、レーザ発振領域における局部的な高い熱によりレーザが故障する原因となります。
レーザ発振領域の温度の管理には通常、温度制御マウントが必要です。しかし、半導体素材の熱伝導率は高くないため、熱がレーザ発振領域に蓄積することがあります。図2で示すように、マウントの温度はピーク出力に影響を与えますが、ロールオーバを防ぐことはできません。
QCLおよびICLの最大駆動電流と最大光出力は、動作条件に依存します。なぜなら動作条件がレーザ発振領域の熱負荷を決定するからです。
最終更新日:2019年12月4日
1
HeNeレーザ:取扱い方と取付け方のガイドライン
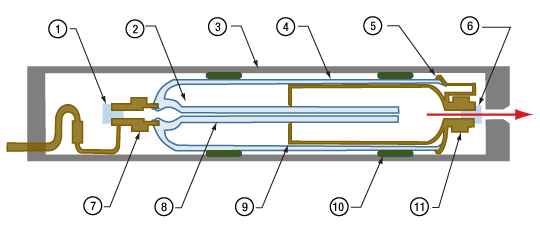
Click to Enlarge
図 3:HeNeレーザの外部筐体は、レーザ共振器の部品と機械的に結合しています。外部筐体への応力は、レーザ共振器部品のミスアライメントと、破損につながる可能性があり、出力ビーム(赤い矢印)の質とパワーに悪影響をおよぼし、最悪、レーザの故障につながる場合があります。
| 1. | 高反射光学素子 | 7. | アノード |
| 2. | ガス溜 | 8. | ガラス製内孔 |
| 3. | 外側の筐体 | 9. | |
| 4. | ガラス | 10. | ポッティングコンパウンド |
| 5. | ガラス-金属封止 | 11. | カソード |
| 6. | 出力光学素子 |
HeNeレーザは、損傷を防ぐために慎重な取扱いと取付けが必要です。
レーザ筐体には決して曲げ力を加えてはなりません。レーザの外部筐体への応力は、レーザ共振器内部品のミスアライメントや、損傷につながる場合があります。これにより下記に影響をおよぼす恐れがあります。
- 出力ビーム品質への影響
- 出力パワーの低下
- ビームポインティングへの影響
- マルチモード成分の誘因
工場では、HeNeレーザを輸送時の衝撃や振動から保護するための梱包が行われ、十分に保護されておりますが、HeNeレーザの損傷につながるような応力がかかってしまう可能性は、お客様が直接取り扱うときに最も高くなります。
HeNeレーザの最適な性能維持のため、落としたり、力づくで取付け具に挿入しないようにしてください。マウントへの取り付け、ケージ部品やリングアクセサリの使用による筐体の固定、輸送、保管時には十分にご注意ください。
HeNeレーザを丁寧に扱うことにより、長期にわたって最適な性能を得ることができます。
最終更新日:2019年12月4日
2
チョッパーホイールを使用したビームサイズの測定法
Click to Enlarge
図5:ブレードは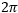 fの角回転速度で、Rθの弧(Rはブレード中心からの距離)をトレースします。図のチョッパーホイールは、MC1F2です。
fの角回転速度で、Rθの弧(Rはブレード中心からの距離)をトレースします。図のチョッパーホイールは、MC1F2です。
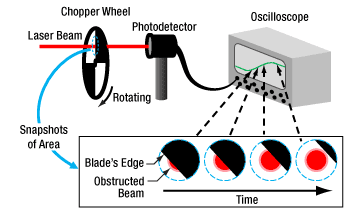
Click to Enlarge
図4:上記に示すセットアップでおおよそのビームサイズの測定が可能です。チョッパーホイールのブレードがビーム横切るとき、S字状の曲線がオシロスコープに現れます。
Click to Enlarge
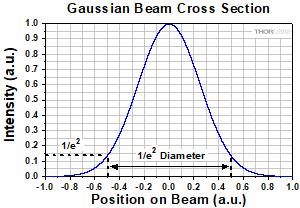
図7:ガウシアンビームの直径は1/e2強度の幅で表されます。
Click to Enlarge
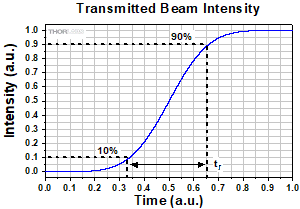
図6:信号の立ち上がり時間(tr )は、通常、強度の10%~90%の時間で定義されます。立ち上がり時間はホイールの回転速度とビーム径に依存します。
カメラや走査スリット型ビームプロファイラはビームサイズやビーム形状を特性化するツールですが、ビームサイズが小さすぎたり、動作範囲外の波長においては正確な測定を行うことができません。
ビームサイズの正確な測定にはチョッパーホイールやフォトディテクタ、オシロスコープが使用されます(図4)。回転するチョッパーホイールがビームを通過すると、S字状の軌跡がオシロスコープに表示されます。
ブレードがθ の角度を掃引すると、S曲線の立ち上がりまたは立ち下がり時間は、ブレードの移動方向に沿ったビームのサイズに比例します(図5)。 ホイールの中心からR の距離にあるブレードエッジ上の点は、ビームサイズにほぼ等しい弧の長さ分(Rθ )、ビームを横切ります。
このビームサイズ測定をするためには、ディテクタとオシロスコープを合わせた応答を、信号の変化の速度よりもはるかに速くする必要があります。
例:S曲線の立ち上がりエッジ
ビームに関連する角度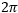 ftr )
ftr )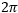 ftr )
ftr )
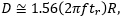
10%~90%の強度間で定義されたビーム径の1.56倍となります。
最終更新日:2021年6月22日1
Content improved by our readers!
レーザ光に薄レンズの公式を適用できるか
レーザ光に対しては、従来の薄レンズの公式よりも、回析を考慮に入れた、修正された薄レンズの公式を使用することをお勧めいたします。この修正された公式はレーザ光をガウシアンビームとして取り扱っており、多くのシングルモードレーザやファイバ出力型レーザ光源に適しています。また、修正された公式はレーザ光が完全なガウシアンの強度プロファイルを有していない場合でも適用可能です。[1]
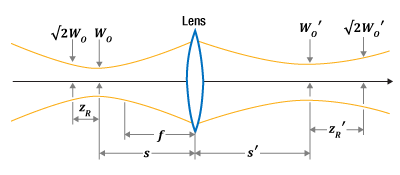
Click to Enlarge
図1:焦点距離がf の薄レンズがガウシアンビーム内に挿入されています。修正された薄レンズの公式では、物体は入射光のビームウェストに相当し、その位置はレンズの入射側からs の距離にあります。入射ビームの半径(W )は、ビームウェストの位置ではWoで、レイリー長の範囲(±zR )ではそれほど大きく変化しません。像は出射光のビームウェストに相当し、その位置はレンズの出射側からs 'の距離にあります。出射ビームの半径(W ')は、ビームウェストの位置ではWo'で、レイリー長の範囲(±zR')ではWo 'からそれほど大きくは変化しません。
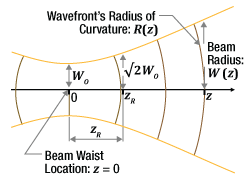
Click to Enlarge
図3:半径W(z)や波面の曲率半径R(z)などのガウシアンビームのパラメータは、ビームウェストからの距離zを用いて計算されます。 ビームウェストは常に原点に位置します。
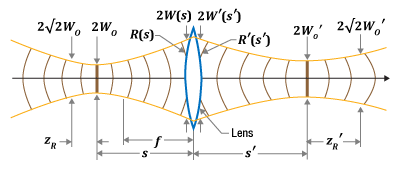
Click to Enlarge
図2: このモデルの重要な点は、レンズにおける入射ビームと出射ビームの関係です。2つのビームの半径は同じで、ビームの波面曲率はレンズの焦点距離と関係します。波面の曲率半径はビームウェストではフラット(太い垂直線)であり、ビームウェストから遠ざかるほど徐々に球形になります。
| Ray-Optics Thin-Lens Equation | ||||
| Conventional Thin-Lens Equation | 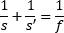 | |||
| Gaussian Beam Equations | Lens System Relations | |||
| Beam Radius | 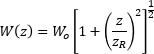 | Beam Radii at Lens |  | |
| Wavefront's Radius of Curvature |  | Wavefront Curvatures at Lens |  | |
| Rayleigh Range | 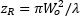 | Magnification (m ) | 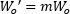 | |
| Gaussian Beam Thin-Lens Equations | ||||
| Modified Thin-Lens Equation | Input Beam Perspective | 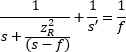 | ||
| Output Beam Perspective | 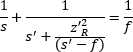 | |||
| Magnification | 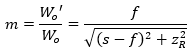 | |||
物体、像、およびレーザービーム
従来の薄レンズの公式(表、上段)は光線光学モデルをベースにしており、レンズの焦点距離(f )用いて、レンズと物体の間の距離
修正された薄レンズの公式では、それらの距離がレンズと入射光および出射光の各ビームウェストとの距離に対応します(図1)。ビームの半径はビームウェストの位置で最小となり、ビームウェストから遠ざかるにつれて大きくなります。ビーム内にレンズを置くと、新たなビームウェストと発散特性を有するビームが出射されます。入射ビームのウェスト半径(Wo )は物体のサイズ、出射ビームのウェスト半径(Wo' )は像のサイズとして扱われます。
修正された公式には、入射側のレイリー長
修正された薄レンズの公式
T入射光と出射光はガウシアンビームとして伝搬することを仮定しています(図2)。 修正された公式は、レンズに対する入射ビームおよび出射ビームの特性(表、中段)を関係付けることで導かれます。
- レンズの入射面と出射面におけるビーム半径は同じです。
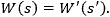
- レンズの焦点距離は、レンズに入射する波面の曲率半径(R )と、レンズから出射する波面の曲率半径(R ')とを関係付けます。

- 倍率(m )は出射ビームと入射ビームのビームウェスト半径(または直径)の比です。
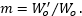
なおビーム半径(W )と波面の曲率半径(R )は、ビームウェストからの相対距離(z )を用いて計算されることにご留意ください。修正された薄レンズの公式が2つあるのは(表、下段)、入射ビームパラメータ(zRとs )または出射ビームパラメータ(zR 'とs ')のどちらが既知であるかによって式が異なるためです。
完全なガウシアンではないレーザービームのレイリー長は、同じビームウェスト半径を有する理想的なガウシアンビームのレイリー長よりも短くなります。この2つの値の比であるM2は、しばしばレーザービームの品質を表す仕様として用いられています。ビームのレイリー長にM2の値を乗じ、その積の値を修正された薄レンズの公式におけるzRまたはzR ' として用いてs ' またはsを求めます。
ガウシアンビームの独特な振る舞い
ガウシアンビームは、特に光線光学モデルと従来の薄レンズの公式による予測と比べると、驚くような振る舞いをすることがあります。
例えば、従来の薄レンズ(表参照)の公式においては、物体をレンズ前方の焦点に置いたとき、像は無限遠に生じると予測します。しかしガウシアンビームにおいては、物体側に相当する入射光のビームウェストがレンズからその焦点距離の位置にあるとき、像側のビームウェストはレンズの出射側から焦点距離の位置に生じます。
そのほかにも、従来の薄レンズの公式では、無限遠の位置に像を結ぶことが可能であると予測します。しかし、レイリー長がゼロではないガウシアンビームの場合は、無限遠の位置にビームウェストを生じさせることはできません。その代わり、像のビームウェストの最大距離は、
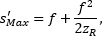
のように入射ビームのレイリー長に依存します。像側のビームウェストがこの距離に生じるようにするには、物体側のビームウェストの位置をレンズの焦点距離よりもさらにレイリー長だけ離れた位置 )
)
参考文献
[1] Sidney A. Self, "Focusing of spherical Gaussian beams," Appl.Opt. 22, 658-661 (1983).
最終更新日:2021年5月20日
CマウントとCSマウントのカメラとレンズに互換性はあるか
Click to Enlarge
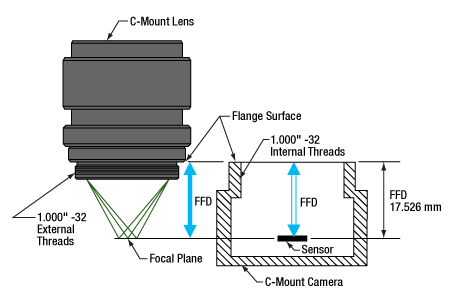
図1:Cマウントのレンズとカメラのフランジバックは同じで、17.526 mmです。そのためレンズを通る光は必ずカメラのセンサ上に焦点を結びます。どちらのコンポーネントにも1.000"-32ネジが付いており、これらは「C-マウントネジ」とも呼ばれます。
Click to Enlarge
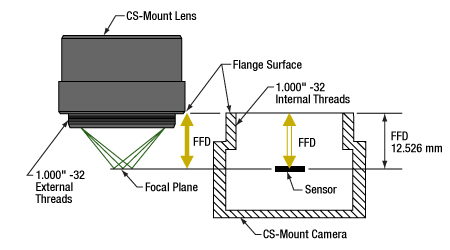
図2:CSマウントのレンズとカメラのフランジバックは同じで、12.526 mmです。そのためレンズを通る光は必ずカメラのセンサ上に焦点を結びます。1.000"-32ネジはCマウントのコンポーネントに付いているネジと同じで、これらは「Cマウントネジ」とも呼ばれます。
CマウントとCSマウントのカメラシステムにはどちらも1.000"-32ネジが付いていますが、この2つのマウントのフランジバック(フランジ焦点距離/FFD、フランジ焦点深度、フランジ-フィルム間距離などとも呼ばれる)は異なります。Cマウントのフランジバックは17.526 mm(図1)、CSマウントのフランジバックは12.526 mm(図2)です。
フランジバックが異なるため、CマウントとCSマウントのコンポーネントには互換性がありません。しかしアダプタを用いることによってCマウントレンズをCSマウントカメラに使用することは可能です。
CマウントとCSマウントの組み合わせ
CマウントとCSマウントのネジ規格は同じですが、マウントの種類が異なるレンズとカメラを直接取り付けることはできません。直接取り付けると、フランジバックが異なるためレンズの焦点面がカメラのセンサ面と一致せず、象がぼやけます。
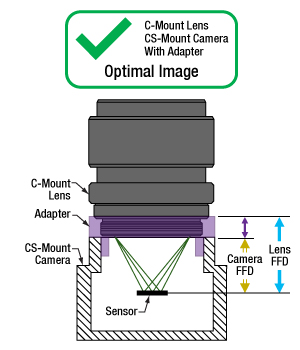
アダプタを使用することで、CマウントレンズをCSマウントカメラに使用することはできます(図3、4)。アダプタによりレンズとカメラのセンサの間隔が5.0 mmだけ長くなり、レンズの焦点面を確実にカメラのセンサ面に一致させることができます。
一方、フランジバックの短いCSマウントレンズは、Cマウントカメラには使用できません(図5)。レンズとカメラの筐体が干渉してカメラのセンサに焦点が合う位置までレンズを近づけることができず、またレンズを近づけられるようなアダプタはありません。
レンズとカメラのパラメータを確認し、互換性のあるコンポーネントなのかどうか、アダプタが必要かどうか、また互換性を持たせる手段はないかを判断することが重要です。
1.000"-32ネジ
インチ規格のネジは、その径とTPI(1インチあたりのネジ山数)によって正確に表現されています。これらの両方のマウントのネジ径は1.000インチ、TPIは32です。Cマウント製品の普及により、1.000"-32ネジは「Cマウントネジ」と呼ばれることがあります。しかし、CSマウントデバイスにも同じネジが用いられているため、この用語は混乱を招く場合があります。
フランジバックについて
フランジバックの値はレンズとカメラの両方について与えられます(図1、2)。レンズの場合、フランジバックはレンズのフランジ面から焦点面までの距離です。フランジ面はレンズ後方のフラットな面で、1.000"-32外ネジとその起点で交差しています。カメラの場合、フランジバックはカメラの前面からセンサ面までの距離です。 レンズがアダプタ無しでカメラに取り付けられているとき、カメラ前方のフランジ面とレンズ後方の面は接触しています。
Click to Enlarge
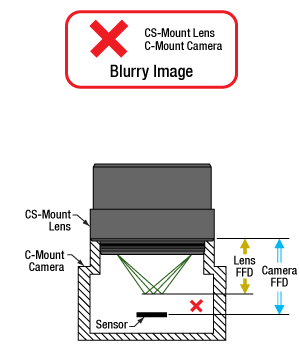
図5:CSマウントレンズをCマウントカメラに直接取り付けると、光はカメラのセンサの手前で焦点を結びます。この場合はフランジバックを青色の矢印の距離だけ短くする必要がありますが、これはアダプタなどでは対処できません。
Click to Enlarge
図4:紫色の矢印が示す距離に相当する適切な厚さのアダプタを使用すると、Cマウントレンズの位置はCSマウントカメラのセンサから最適な位置に配置されます。これによりフランジバックが異なっても、光はカメラのセンサ上に焦点を結ぶことができます。
Click to Enlarge
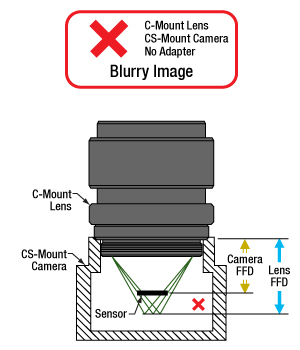
図3:CマウントレンズとCSマウントカメラは、レンズのフランジバック(青色の矢印)とカメラのフランジバック(黄色の矢印)が異なるため、直接取り付けることはできません。光はカメラのセンサ上に焦点を結ばす、像がぼやけます。
最終更新日:2020年7月21日
当社のサイエンティフィックカメラにアダプタは必要か
Click to Enlarge
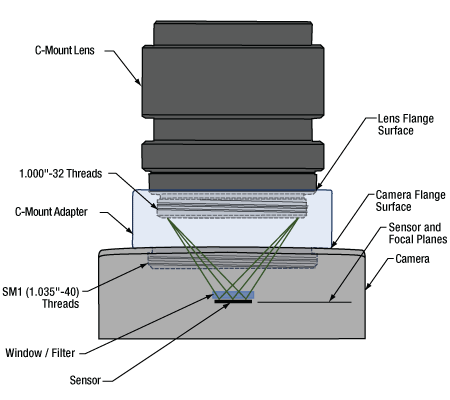
図6:アダプタを使用することで、フランジバックが17.526 mmよりも短いカメラに対して、Cマウントレンズを適切な位置に配置することができます。この図は、ZeluxカメラとアダプタSM1A10Zをもとに描かれています。
Click to Enlarge
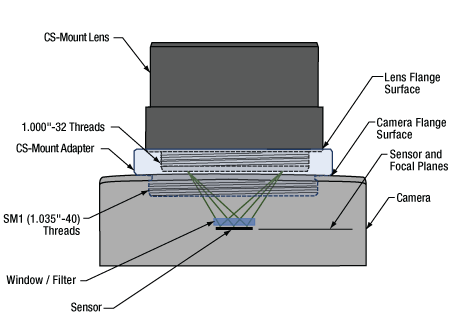
図7: アダプタを使用することで、フランジバックが12.526 mmよりも短いカメラに対して、CSマウントレンズを適切な位置に配置することができます。この図は、ZeluxカメラとアダプタSM1A10をもとに描かれています。
当社のサイエンティフィックカメラKiralux™およびQuantalux®は、すべてCマウントレンズに対応するように予め設定されています。これらのパッシブ冷却方式のカメラからCマウントアダプタを取り外すと、フランジ内のSM1内ネジがご利用いただけます。サイエンティフィックカメラZelux®の取付けフランジにもSM1内ネジが付いています。またCマウントアダプタやCSマウントアダプタもご利用いただけます。
カメラ筐体にはSM1ネジが付いており、これによって当社のコンポーネントで構成されたレンズアセンブリを容易に使用することができます。アダプタを使用すれば、カメラのCマウント構成を変えることも可能です。用途に特化したレンズアセンブリを設計する場合や、そのカメラ用に設計されたものではないアダプタを使用しようとする場合には、カメラとレンズのフランジバック(FFD)が一致し、またカメラセンサのサイズが視野に適していることを確認することが重要です。
カメラとそのアダプタ
ZeluxカメラをCマウントやCSマウント規格に適合する構成に変換するための固定式アダプタをご用意しております(図6、7)。これらのアダプタは、パッシブ冷却方式のKiraluxおよびQuantaluxカメラに付属する調整機能付きCマウントアダプタと同様に、それぞれのカメラ専用に設計されています。
SM1ネジを1.000"-32ネジに変換するアダプタであれば、どの様なものでもカメラにCマウントやCSマウントのレンズを取り付けることが可能ですが、すべてのネジアダプタがレンズの焦点面を特定のカメラのセンサ面に一致させることができるわけではありません。場合によっては、それらの面を一致させられるアダプタが無いことがあります。例えば、こちらのサイエンティフィックカメラでは、ZeluxカメラだけがCSマウントレンズ用の構成にすることができます。
レンズの焦点面の位置は、空気中で測定されるレンズのフランジバックと、レンズとカメラセンサ間に置かれた屈折率を有する全ての光学素子との組み合わせで決定されます。レンズによって集光される光が屈折率を有する光学素子を透過すると、空気中を伝搬する場合とは異なり、焦点面はより遠い位置に移動します(この距離は算出可能)。 このアダプタは、カメラのフランジバックが短いときに、そのフランジバックの長さと、レンズとセンサ間のウィンドウやフィルタによって生じる焦点移動の両方を補正するのに十分な距離を付加するものでなければなりません。
調整機能付きCマウントアダプタ
パッシブ冷却方式のカメラKiraluxおよびQuantaluxは、SM1内ネジ付きカメラ、固定リングで固定されたウィンドウまたはフィルタ(センサの覆い)、および調整機能付きCマウントアダプタから構成されています。
調整機能付きCマウントアダプタの利点は、ウィンドウまたはフィルタと固定リングが取り付けられている時に、レンズとカメラ間の距離を1.8 mmの範囲で調整できることです。調整可能なことで、カメラのセンサ面とレンズの焦点面のミスアライメントによる様々な影響を補正することができます。それらの影響には、温度変化による材料の膨張や収縮、累積公差による位置誤差、異なる厚さや屈折率のウィンドウまたはフィルタに交換したことに伴う焦点シフトなどが含まれます。
無限遠にある物体の鮮明な像を得るためには、カメラのアダプタの調整が必要な場合があります。物体が無限遠にある場合には入射光は平行光であり、レンズのフランジバックは焦点の位置で決定されます。レンズやカメラの実際のフランジバックが意図したフランジバックと一致していない場合があり、無限遠の物体が焦点を結ぶ面がセンサ面からシフトし、そのため像がぼやけてしまうことがあります。
レンズの焦点調整をしても無限遠の物体の鮮明な像が得られない場合には、カメラのアダプタで調整してみてください。アダプタで調整することで公差や環境によるシフトが補正され、像の焦点を合わせることができます。
最終更新日:2020年8月2日
フランジバックがカメラのフランジとセンサ間の距離よりも短くなり得る理由は
カメラとレンズのフランジバック(FFD)を決めるときは、レンズとカメラのセンサ面の間にあるのは空気のみであることを仮定しています。レンズとカメラのセンサの間にウィンドウまたはフィルタ、あるいはその両方が挿入されている場合は、カメラのフランジとセンサ面の間の距離を仕様で指定されたフランジバックよりも長くする必要があるかもしれません。ウィンドウやフィルタにより光路が屈折して焦点面がより遠い位置にシフトするため、フランジバックと同じ距離では短すぎる場合があります。
レンズとカメラセンサの間の光学素子を変更するなら、焦点面のシフト量を計算し、アライメントを保つためにレンズとカメラ間の距離を調整する必要があるかどうか判断してください。焦点の合った像を得るには、適切なアライメントは必要です。理由は、光学素子を変更することで収差やその他の影響が現れ、画像品質が許容できないレベルに低下することがあるためです。
Click to Enlarge
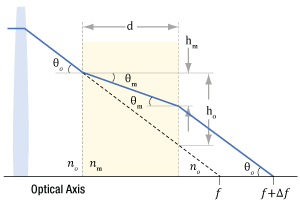
図9:屈折率の違い(θm vs. θo )により光線が屈折するため、光線の光軸に対する角度は空気中よりも媒質内で浅くなります(nm vs. no )。媒質内でdの距離を伝搬したとき、光線は hm しか光軸に近くなりません。そのため、光線はfの位置よりもΔfだけ遠い位置で光軸と交差します。
Click to Enlarge
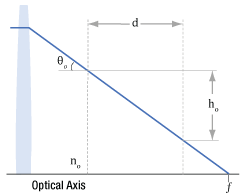
図8:空気中を通る光線は、f.位置で光軸と交差します。光線は距離dを伝搬すると、hoだけ光軸に近くなります。空気の屈折率はno です。
| Example of Calculating Focal Shift | |||
|---|---|---|---|
| Known Information | |||
| C-Mount FFD | f | 17.526 mm | |
| Total Glass Thickness | d | ~1.6 mm | |
| Refractive Index of Air | no | 1 | |
| Refractive Index of Glass | nm | 1.5 | |
| Lens f-Number | f / N | f / 1.4 | |
| Parameter to Calculate | Exact Equations | Paraxial Approximation | |
| θo | 20° | ||
| ho | 0.57 mm | --- | |
| θm | 13° | --- | |
| hm | 0.37 mm | --- | |
| Δf | 0.57 mm | 0.53 mm | |
| f + Δf | 18.1 mm | 18.1 mm | |
| Equations for Calculating the Focal Shift (Δf ) | ||
|---|---|---|
| Angle of Ray in Air, from Lens f-Number ( f / N ) |  | |
| Change in Distance to Axis, Travelling through Air (Figure 8) | 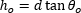 | |
| Angle of Ray to Axis, in the Medium (Figure 9) | 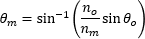 | |
| Change in Distance to Axis, Travelling through Optic (Figure 9) |  | |
| Focal Shift Caused by Refraction through Medium (Figure 9) | Exact Calculation | 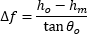 |
| Paraxial Approximation |  | |
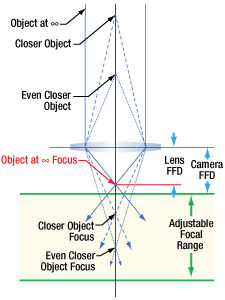
Click to Enlarge
図11:公差や温度の影響により、レンズとカメラのフランジバックが異なることがあります。レンズのフランジバックの方が短い場合には、無限遠の物体の像は焦点調整範囲外になります。このシステムでは焦点を合わせられないため、像はぼやけます。
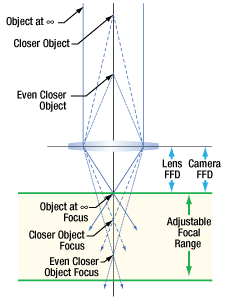
Click to Enlarge
図10:カメラとレンズのフランジバックが同じときは、カメラのセンサ面とレンズの焦点面は完全に一致しています。無限遠の物体の鮮明な像は、システムの焦点調整範囲の一端で得られます。
屈折による焦点移動
光が固体媒質を通るときの光路は直線です(図8)。光が焦点に集光していく過程で、光線の光軸に対する角度
平行平面を有する屈折率の高い
光学素子を通るときの光線は、同じ距離だけ空気を通る光線に比べて、光軸に向かう速さは遅くなります。光学素子から出た後の光線の光軸に対する角度は、また光学素子を通過していないときの角度θoになります。しかし、光学素子から出る光線の位置は、光学素子を通らない場合には決して通ることのない、光軸からより遠く離れた位置になります。光学素子によって屈折された光線は光軸からより遠くなるため、光軸と交差する位置は光学素子を通らない光線よりもΔfだけ先にシフトします。光学素子の厚さが増すと、2つの光線の間は広がり、Δfは増大します。
無限遠およびそれを超えた調整
カメラシステムでは、多くのアプリケーションにおいて、無限遠の物体の高品質な像を得ることが要求されます。これらの物体からの光線は平行光で、近い物体からの光線よりもよりレンズに近い位置で焦点を結びます(図10)。カメラとレンズのフランジバックは、無限遠の位置にある物体からの光線の焦点が、カメラのセンサ面と一致するように決められています。レンズに焦点の調整範囲があるときには、その範囲の一端は無限遠の物体に、もう一端はそれよりも近い物体に焦点が合うように調整されています。
温度変化や累積公差などの影響により、レンズやカメラのフランジバックが仕様を満たさない場合があります。レンズの実際のフランジバックがカメラのフランジバックよりも短いときには、カメラのシステムは無限遠の物体の鮮明な像を得ることはできません(図11)。このオフセットは、レンズとカメラセンサの間にある光学素子を取り外したときも生じることがあります。
これを補正するために、レンズによっては焦点を結ぶ物体の位置を、無限遠を「超えて」設定できるようにしています。これは物理的な距離を意味しているわけではなく、単にレンズの焦点面をより遠くまで移動できるようにしているだけです。当社のKiralux™とQuantalux®カメラに付属する調整機能付きCマウントアダプタは、必要に応じて距離を調整できるようになっています。
レンズのフランジバックがカメラのフランジバックよりも長い場合には、無限遠の物体の像はシステムの焦点調整範囲内にありますが、本来は焦点調整範囲内にあるべき近い物体がその範囲外になります。この状況は、レンズとカメラセンサの間に光学素子を挿入することで生じる場合があります。無限遠の物体のイメージングが可能であるならば、この状況はしばしば許容されることがあります。
カメラの設計例
ハーメチックシールされたTE冷却型のCマウントQuantaluxカメラには、フランジ面とセンサ面の間に18.1 mmの固定された距離があります。しかし、Cマウントカメラシステムのフランジバック(f )は17.526 mmです。フランジバックよりも長い距離が必要であることは、ハーメチックカバーにはんだ付けされているウィンドウとセンサを覆うガラスによる焦点移動を考慮すると明白です。図9の下の表に記載されている結果は、厳密な式でも近軸近似の式でも、必要な全体の距離として18.1 mmという値が得られることを示しています。
最終更新日:2020年7月31日
手動ステージを電動ステージに変換する方法
当社の手動ステージはマイクロメータやその他のアジャスタで移動させますが、それらは移動量とバレル径が適合した電動アクチュエータに交換することができます。交換する前に、取り付けられているアジャスタを完全に手元側に引き寄せて、バネのエネルギーを突然解放することで生じる機械的衝撃からステージを保護することが重要です。
動画1: まず取り付けられているマイクロメータやその他のアジャスタを完全に手元側に引き寄せておくことが重要です。アジャスタが伸びた状態でステージから取り外すと、上部プレートは後方のハードストップに向かって一気に引っ張られます。衝突による衝撃はステージの破損につながる場合があります。
動画3:ステージXR25P(/M)のマイクロメータを完全に手元側に引き寄せた後、ステージのバレルクランプの固定用キャップスクリュを2 mm六角レンチで緩めてアジャスタを取り外します。電動アクチュエータ(この例ではDCサーボモータ駆動のZ825Bを使用)のバレルを挿入し、ロック用止めネジを適度に締め付けます。
動画2:ステージMT1B(/M)の調整ネジを完全に手元側に引き寄せた後、ステージのバレルクランプの固定用キャップスクリュを3/32インチ六角レンチで緩めてアジャスタを取り外します。電動アクチュエータ(この例ではステッピングモータ駆動のZFS13Bを使用)のバレルを挿入し、ロック用止めネジを適度に締め付けます。
バレル径と移動量が適合するか確認する
これらのステージはバレルクランプでアクチュエータを固定するため、アクチュエータのバレル径がクランプの仕様に適合することが必要です。デモで使用しているステージはどちらも3/8インチ(9.5 mm)バレルのアクチュエータが適合します。
アクチュエータの移動量はステージの移動量を超えてはいけません。移動量がステージよりも大きいアクチュエータを使用すると、ステージの限界を超えて移動させようとする可能性が生じ、アクチュエータのモータとステージの両方を破損させる恐れがあります。移動量がステージよりも小さいアクチュエータを使用した場合は、アクチュエータもステージも破損する恐れはありませんが、ステージの移動範囲は狭くなります。こちらのデモで使用している直線移動ステージMT1B(/M)およびXR25P(/M)の移動量は、それぞれ13 mmと25 mmです。
ステージの損傷を防止するためにアジャスタを手元側に引き寄せる
作業を開始する前に、取り付けられているアジャスタを完全に手元側の位置に引き寄せ、ステージ損傷の原因となりうる1つの大きな要因を排除します。アジャスタが完全に手元側に引き寄せられている場合、上部プレートは最後方の位置にあり、バネの張力は緩和されています。アジャスタの先端がステージに接触しなくなるのが理想的です。
アジャスタが伸びた状態では、ステージ内部のバネの力が作用して危険です。バネの力により、上部プレート(すなわち可動部)とアジャスタ先端の接触が保たれています(動画1)。アジャスタが伸びた状態でステージから取り外すと、上部プレートはバネによって後方のハードストップに向かって引っ張られます。この衝突による機械的衝撃は重大な場合があり、ステージ部品のミスアライメント、ボールベアリングへの影響、あるいはステージ移動時における角度偏差の発生といった問題が生じる可能性があります。
交換する
取り付けられているアジャスタを完全に手元側に引き寄せた後、ステージMT1B(/M)またはXR25P(/M)のバレルクランプの固定用キャップスクリュをそれぞれ3/32インチまたは2 mm六角レンチで緩めます。これによりバレルを保持していた力が緩められ、アジャスタを外すことができます(動画2、3)。
電動アクチュエータのバレルを挿入し、固定用のキャップスクリュを適度に締め付けます。このとき、締め過ぎないように気を付けてください。上部プレートのバネの負荷でアクチュエータがバレルクランプから押し出されてはいけませんが、固定ネジを締め付けすぎるとバレルが変形してアクチュエータの線形性に影響を与える恐れがあります。
移動ステージに関するその他の情報は
こちらの動画ページをご覧ください。
最終更新日:2023年11月11日
デジタルマイクロメータからの位置情報の記録

Click to Enlarge
図 2:上のSBC-COMMパッケージは、デジタルマイクロメータ DM713に表示される位置データを記録するのにご使用いただけます。

Click to Enlarge
図1: バビネソレイユ補償板SBC-VIS(左)にはデジタルマイクロメータDM713(右)が付属しており、補償板のリターダンスを調整するのに使用されます。
DM713などのデジタルマイクロメータは、1つのオプトメカニクスを特定の距離だけ移動するのに便利です。例えば、均等な間隔で試料内の点に光を集光するために、対物レンズの前で試料を保持した移動ステージを移動させる場合があります。
しかし、同時にその位置を記録したい場合もあります。1つの方法は、マイクロメータを開始位置(0)に設定し、必要な距離を移動させてその距離を表示させることです。
DM713のみを使用した場合には、表示を読んで記録するという手順が追加されますが、これは表示が見えないような暗い実験室内では面倒な作業になることがあります。それに対する1つの解決策は、RS-232 インターフェイスケーブルが付属する当社のSBC-COMMを使用することです。 当社では、DM713で距離を連続的に測定するためのプログラムを、Visual C#®およびLabVIEW®を用いて作成する方法を解説したソフトウェアアプリケーションノートを作成しています。
ほかの解決策としては、Mitutoyo®製のSPCケーブル05CZA662と、プッシュボタンおよびUSBインターフェイスケーブルが付いたUSBインプットツールIT-016Uを別途ご購入いただく方法がございます。このデバイスを使用すると、任意のテキスト入力ソフトウェアパッケージを開き、1つのプッシュボタンを押すことで、デバイスがキーボードのように機能してソフトウェアに数値を入力することができます。
最終更新日:2019年12月4日
1
Insights:軸外放物面(OAP)ミラー
スクロールするか下のリンクをクリックすると、軸外放物面(OAP)ミラーの利点や使用方法についてご覧いただけます。
- なぜ球面ミラーではなく放物面ミラーを使うのか?
- 軸外放物面(OPA)ミラーの利点
- OAPミラーの軸外し角
- OAPミラーを使用したコリメート光の集光、および点光源からの光のコリメート
- OAPミラーの光軸と集光軸の特定方法
- OAPミラーをペアで使用すると像のリレーやビームへのアクセスが可能になります
- OAPミラーの取付けとアライメント
- OAPミラーをベースにした反射型コリメータにおける光の方向性
なぜ球面ミラーではなく放物面ミラーを使うのか?
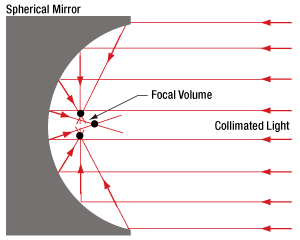
Click to Enlarge
図2:球面ミラーでは、コリメート光のすべての光線が1つの点を通過するように反射することはできません。焦点体積内での光線同士の交差点を、いくつか選んで黒点で示しています。
Click to Enlarge
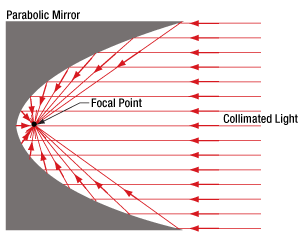
図 1:放物面ミラーでは、コリメート光のすべての光線が1つの焦点に集められます。
放物面ミラーは、点光源からの光をコリメートしたりコリメート光を集光したりする場合には、球面ミラーよりも優れた性能を有します。
コリメート光の集光
放物面ミラー(図1)を用いると、コリメートされている入射光を回折限界スポットに集光することができます。 これに対して球面ミラー(図2)を用いた場合は、コリメートされている入射光を回折限界スポットよりも大きな体積のスポットにしか集光できません。球面ミラーのこの焦点体積(Focal Volume)の大きさは、コリメートされた入射ビームの径を小さくすることで小さくすることができます。
点光源からの光のコリメート
点光源からの光はすべての方向に放射されます。この発散光の光源を放物面ミラーの焦点に置くと、ミラーから出てくる光は非常に良くコリメートされています。理想的な点光源の場合、反射されたすべての光線は互いに完全に平行になります。
点光源を球面ミラーの焦点体積内に置いたときには、ミラーから出てくる光は放物面ミラーと比較してそれほど良くコリメートされません。点光源からの各光線は、球面ミラーで反射されたときには完全な平行にはなりませんが、球面ミラー表面上の近い点で反射された2本の光線は遠い点で反射された2本の光線よりも平行に近い状態になります。そのため、反射面積を小さくすればコリメート光としての品質は向上します。これは焦点体積内の光源から放射される光の角度範囲を制限することと等価です。
放物面ミラーと球面ミラーの選択について
放物面ミラーを選択するのが常に良いとは限りません。アプリケーションにおいて要求されるビーム径、コスト面の制約、スペース上の制限、性能要件など、すべてが選択に影響します。ビーム径が影響するのは、ビーム径が小さいと放物面ミラーと球面ミラーの性能が近くなるためです。放物面ミラーは反射部分の加工がより難しいため、球面ミラーより高価になります。また放物面ミラーのサイズは一般に球面ミラーよりも大きくなります。コストや物理的なサイズの違いに比べて、向上する性能が重要な場合もあれば、重要でない場合もあります。
最終更新日:2019年12月4日
1
軸外放物面(OPA)ミラーの利点
Click to Enlarge
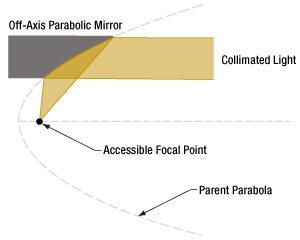
図4:軸外放物面(OAP)ミラーは、大きな放物面の一部分と考えられます。どちらも焦点は同じですが、OAPミラーのほうがよりアクセスしやすくなっています。
Click to Enlarge
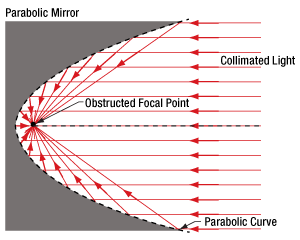
図3:軸対称放物面ミラーの焦点は反射面に近く、また一般に反射面に囲まれているため、焦点にアクセスしにくくなっています。
通常の軸対称放物面ミラーと軸外放物面ミラーは、どちらも1つの焦点を有します。軸外放物面ミラーの利点は、対称な放物面ミラーと違って焦点にアクセスしやすいことです。
焦点が1つであることは放物面ミラーの主たる利点であり、レーザ光を回折限界スポットに集光させることを要求されるイメージングや製造など、様々な用途に利用できます。
焦点周りに対称な通常の放物面ミラーを使用する場合、いくつかのマイナス面があります(図3)。1つは、一般にミラーの側面が妨げとなり、焦点にアクセスできないことです。もう1つは、ミラーを発散光のコリメートに使用したとき、光源の筐体がコリメート光の一部をブロックすることです。特にミラーの光軸に対して小さな角度で放射された光がブロックされます。
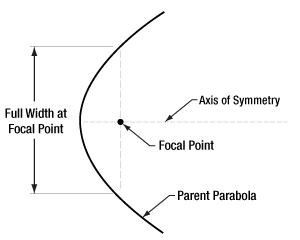
軸外放物面ミラー(図4)を使用するのは、このような問題の解決策の1つです。このミラーの反射面の形状は放物面ですが、焦点周りに対称ではありません。OAPミラーの反射面は、焦点から離れた位置にある親放物面(Parent Parabola)上の一部分に対応します。どの部分の面を選択するかは、焦点とミラー中心間の角度や距離に対する要求に依存します。
最終更新日:2019年12月4日
OAPミラーの軸外し角
Click to Enlarge
図 6:放物面の幅は、軸に垂直な焦点を通る線に基づいて測定するのが一般的です。
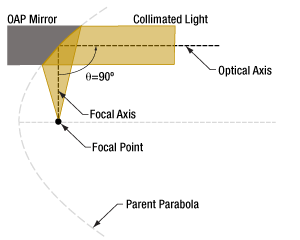
Click to Enlarge
図 5:こちらのOAPミラーの軸外し角は90°です。
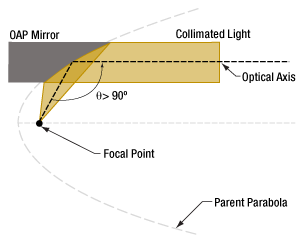
Click to Enlarge
図8:放物面の幅を小さくすると軸外し角が大きくなります。図6と比較してみてください。
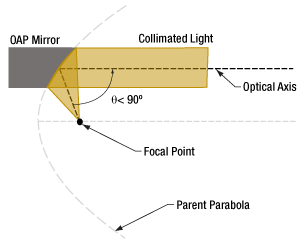
Click to Enlarge
図7:放物面の軸に近い部分を選択すると軸外し角は小さくなります。
OAPミラーの軸外し角(θ )は、ミラーの光軸と集光軸の間の角度です。この角度は、OAPミラーとして使用される親放物面(Parent Parabola)上のセグメントと、親放物面の幅(図6)に依存します。図5におけるOAPミラーの軸外し角は90°です。
放物面セグメントと焦点の近接について
焦点により近い放物面セグメントを選択すると、軸外し角は小さくなります。図7におけるミラーの軸外し角は図5のミラーに比べて小さいですが、この2つの図で唯一異なるのは図7でOAPミラー用に選択された親放物面上のセグメントが焦点により近いことです。
親放物面上のセグメントの位置によって焦点距離も変化します。焦点に近い放物面セグメントを選択すると、ミラー中心と焦点の間の距離が短くなります。
親放物面の幅
親放物面の幅を大きくすると軸外し角が小さくなります。その関係を図7と8で示しています。図7の放物面の幅は大きいく、それに対してミラーの軸外し角は小さくなっています。
親放物面の幅は焦点距離にも影響します。放物面の幅が大きくなると、焦点距離は長くなります。
軸外し角について
OAPミラーの軸外し角は90°で設計されていることが多いですが、90°未満のOAPミラーも一般的です。
最終更新日:2019年12月4日
3
OAPミラーを使用したコリメート光の集光、および点光源からの光のコリメート
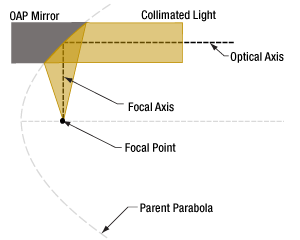
Click to Enlarge
図 9:OAPミラーの集光軸と光軸は一致せず、平行でもありません。
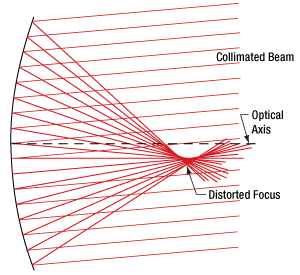
Click to Enlarge
図 11:入射するコリメートビームがミラーの光軸に対して平行でない場合、回折限界スポットは得られません。集光する領域が広がってしまいます。
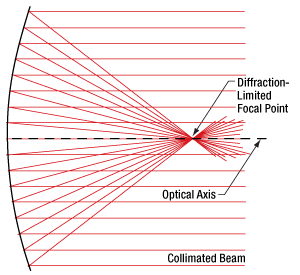
Click to Enlarge
図 10:入射するコリメートビームが放物面ミラーやOAPミラーの光軸に対して平行な場合、光は回折限界スポットに集光されます。
放物面ミラーや軸外放物面(OAP)ミラーでは、適切なビームが適切な軸に沿って入射された場合にのみ、期待するコリメートビームや回折限界集光スポットが得られます。
放物面ミラーとOAPミラーの比較
OAPミラーの反射面は親放物面(Parent Parabola)の一部であり、その中心位置は親放物面の光軸上にはありません(図9参照)。図10は標準的な放物面ミラーの図です。
OAPミラーの光軸は親放物面の光軸に対して平行ですが、互いに離れています。しかし、OAPミラーの焦点と親放物面の焦点とは一致しています。
OAPミラーの集光軸は焦点とOAPミラーの中心を通ります。OAPミラーの集光軸と光軸は平行ではありません。一方、反射面が親放物面の光軸の中心にある標準的な放物面ミラーでは、それらの軸は一致しています。
コリメート光の集光
放物面ミラーやOAPミラーを使用してコリメート光を回折限界スポットに集光する場合、光はミラーの光軸に沿って入射する必要があります(図9と図10を参照)。
入射するコリメート光が光軸に対して平行でない場合は、1点に集光されません(図11参照)。
OAPミラーの集光軸に沿ってコリメート光を入射したり、あるいは光軸に対して平行ではない光を入射したりすると、光を回折限界スポットに集光することはできないため、当社ではそのような使い方はお勧めしていません。
点光源からの光のコリメート
点光源から良好なコリメート光を得るには、点光源をミラーの焦点に置く必要があります。
点光源をOAPミラーの光軸上に置いたり、焦点ではない位置に置いたりした場合は、点光源からの光を良好にコリメートすることはできません。
OAPミラーは、その原点がミラーの焦点と一致するような球面波もコリメートすることができます。
最終更新日:2019年12月4日
4
OAPミラーの光軸と集光軸の特定方法
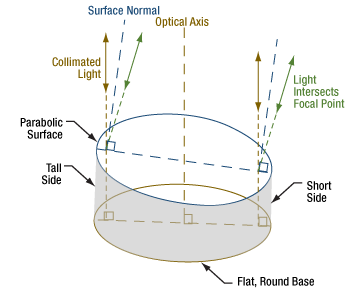
Click to Enlarge
図13:光軸の方向はミラー基板のベースに対して垂直であることに留意することで特定できます。焦点位置は、光軸に対して平行に入射するコリメート光の光線を考慮することで推定できます。これらの光線は、局所面法線に対して対称な方向に反射され、ミラーの焦点を通過します。

Click to Enlarge
図 12:OAPミラーのベースはフラットで、その形状は円形であり、側面の高さは一定ではありません。フラットなベースはミラーの光軸に対して垂直です。上はMPD2151-P01です。
軸外放物面(OAP)ミラーを使用するときに、光軸と集光軸を特定するのが困難な場合があります。特にミラーの放物面の曲面が見えにくい場合には困難です(図12参照)。
ミラー基板の物理的な特性や寸法は、ミラーを配置したりアライメントしたりする際の指標として有用です。
ミラー基板のベース側はフラットで、形状は円形です。光軸はそのフラットなベースに対して垂直です。従って、コリメート光はベース面に対して垂直に入射する必要があります。
基板の側面は高い部分と低い部分があり、反射面は傾斜しています。反射面の様々な位置での面法線は、表面を目視することで大まかに推定することができます(図13)。
焦点位置は、光軸に対して平行に入射したコリメート光の光線が、ミラーの表面で反射される様子を考えることで推定することができます。入射光は面法線に対して対称な方向に反射されます。そして反射光は焦点を通ります。ミラー側面の高い位置と低い位置の近傍からの2本の光線をイメージして追跡することで、焦点の位置を推定できます。
当社のOAPミラーの取付けおよびアライメントの方法
当社のOAPミラーの底面には、1つのアライメント用の穴と、3つの取付け用のタップ穴が加工されています。タップ穴は正三角形の頂点位置に配置されており、ネジの切られていないアライメント用の穴の位置はOAPミラーの短い側面の位置を示しています。タップ穴はミラーをアダプタや取付けプラットフォームに固定できるように設計されています。
最終更新日:2019年12月4日
5
OAPミラーをペアで使用すると像のリレーやビームへのアクセスが可能になります
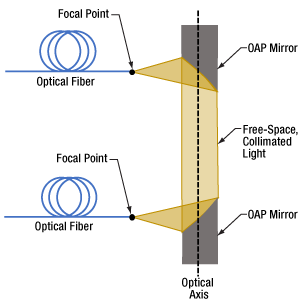
Click to Enlarge
図15:OAPミラーのペアを用いると、1本のファイバから光を出射させ、他のファイバにその光を入射することができます。これにより、バルク光学素子を光路に挿入する必要があるときなどに、ビームにアクセスすることが可能になります。ファイバのコア径は小さいため、ファイバ端面から出射される光は点光源に近くなります。
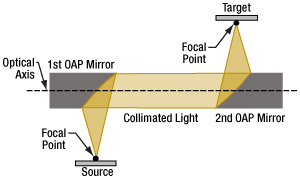
Click to Enlarge
図14:OAPミラーのペアはイメージング用としてや、ビームのリレー用として使用することができます。
像のリレー
OAPミラーをペアで使用すると、ミラー間を伝搬する光がコリメートされるため、図14および図15に示すようにリレー光学系として機能します。OAPミラーは焦点からの光をコリメートするか、またはコリメート光を集光するためだけに設計されているため、光源も結像光もコリメートされていない場合はOAPミラーを2つ使用する必要があります(有限共役結像)。
2つのOAPミラーを使用した場合、ミラー間の距離の調整が容易になります。コリメート光の光路は、フィルタや他の光学素子を挿入するのにも便利です。もう1つの利点は、2つのミラー間の距離を調整することで、システムのアライメントを乱すことなく、ソース面上やターゲット面上の焦点位置を移動することができることです。
ファイバーネットワーク内のビームへのアクセス
OAPミラーのペアを用いて、光ファイバーシステム内の光にアクセスできる自由空間光の光路を作ることができます。図15はその構成例で、必要なフィルタや他のバルク光学素子をビーム光路に挿入するのに便利です。自由空間光の光路長はアライメントを乱すことなく調整することができます。
このシステムをセットアップするとき、ファイバ端面のコアがそれぞれソース側とターゲット側の焦点と一致するようにアライメントしなければなりません。また、両方のミラーでコリメートされた光の光路は同一線上にあり、完全にオーバーラップする必要があります。
この構成はファイバ用光学フィルタ/減衰器マウントの基本形です。
最終更新日:2019年12月4日
OAPミラーの取付けとアライメント
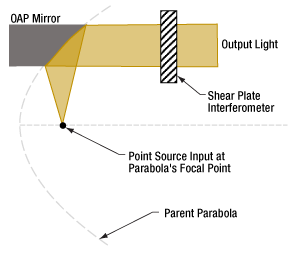
Click to Enlarge
図 17:OAPミラーを使用して点光源をコリメートするとき、出力ビームにシヤリング干渉計を置くと、アライメントが容易になります。

Click to Enlarge
図 16:OAPミラーの反射面の形状は、親放物面の焦点から離れた位置を中心とする親放物面の一部分に一致します。そのため、OAPミラーの反射面は回転対称ではありません。ミラーを取付けるときには、ミラーがその光軸周りに回転しないように注意しなければなりません。
OAPミラーは回転対称ではありません。これは、ミラーの反射面として親放物面の焦点から離れた一部分を用いているためです(図16参照)。反射面のこの非対称性により、OAPミラーが回転すると焦点位置も回転します。そのようなことが生じれば光学システムの性能低下につながるため、ミラーは反射面が光軸周りに回転しないように固定する必要があります。
ミラーの光学性能は、他の5つの自由度のアライメントについても、そのドリフトの影響を受けます。アライメントのドリフトを防止する方法の1つは、キネマティックマウントではなく、固定マウントを使用することです。
シヤリング干渉計は、OAPミラーを点光源の入射光にアライメントするときに役立ちます。この干渉計はコリメート光の品質を評価するために出力ビーム上に置かれます(図17)。コリメートビームの品質が最適化させると、アライメントも最適化されています。
最終更新日:2019年12月4日
OAPミラーをベースにした反射型コリメータにおける光の方向性
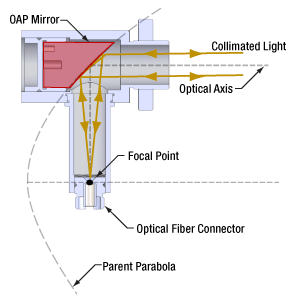
Click to Enlarge
図 19:コリメータの反射光学素子はOAPミラーです。ミラー基板は赤で示されています。この反射面は、放物面の頂点から離れた位置の放物面の一部分です。親放物面とOAPミラーの焦点は一致しています。
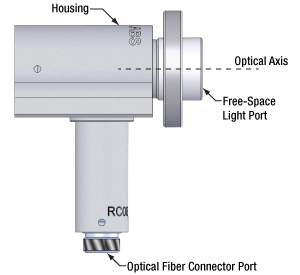
Click to Enlarge
図18:当社ではファイバーコネクタ用のポートと、光軸に対して平行に伝搬するコリメートされた自由空間光用のポートを備えた、反射型コリメータをご用意しています。
当社の反射型コリメータの2つのポートは入れ替えることができません。1つのポートには光ファイバのコネクタを取付けますが、そこでは発散光を放出する点光源であることが要求されます。もう1つのポートはコリメートされた自由空間光用として設計されています(図18参照)。
自由空間光用ポート
このポートに入射する光は、光軸に対して平行なコリメート光でなければなりません。ファイバ端面、半導体レーザやその他の光源などからの発散光は入射しないでください。そのような光はファイバーコネクタ用のポートではコリメートされておらず、またファイバーポートに接続されたファイバに結合もされません。
ファイバーコネクタ用ポート
このポートではファイバの端面がミラーの焦点にアライメントされます。ファイバの端面は焦点に置かれた点光源に近いため、自由空間ポートからはコリメートされたビームが出射されます。ファイバ端面を焦点にアライメントすることは、自由空間光用ポートからの光がコリメートされ、光軸に対して平行に出射される理由でもあります。
光の方向性について
コリメータにおける光の方向は、反射素子として回転非対称の軸外放物面(OAP)を使用していることで決まっています(図19)。断面図では、ファイバの端面がOAPミラーの焦点でもある親放物面の焦点に置かれていることを示しています。
最終更新日:2019年12月4日
ファラデー効果の大きさを測定する方法
ファラデー効果を有する物質を磁場中に置き、光を伝搬させると光の偏光方向が回転します。物質内のファラデー効果の大きさを測定する1つの方法は、物質に直線偏光の光を入射し、強い磁場を印加して出射光に現れる偏光方向の変化を観察するものです。偏光方向の変化を決定するために、物質からの出射光の偏光状態を直接測定する必要はありません。その代わりに、回転する直線偏光子を透過した光パワーを測定することで出射光の状態を解析することができます。測定される光パワーは振動しますが、その位相は回転する偏光子に入射する直線偏光の偏光方向に依存します。この方法による測定をCdMgTeの結晶を使用して実施しました。結晶からの出射光の測定結果を用いて、物質のファラデー効果の大きさを特徴付けるベルデ定数を算出しました。
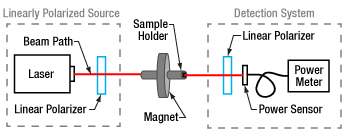
Click to Enlarge
図1: ファラデー効果は、直線偏光の光源と偏光状態の検出システムとの間に試料を置くことで測定できます。CdMgTe結晶の長さは環状磁石の穴の長さの1/3ほどで、プラスチック製のサンプルホルダを用いて穴の中心に固定しました。検出システムでは、光パワーセンサを目盛付き回転マウントに取り付け、できるだけ直線偏光子の出射側に近接して設置しました。このセットアップの利点は、アライメント作業が最小限で済むことです。
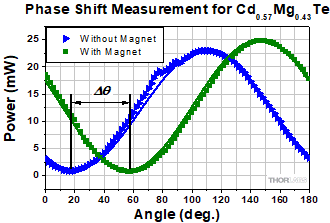
Click to Enlarge
図3: 検出用偏光子の透過軸を回転し、2°ごとに光パワーを測定しました。磁石を使用しなかった場合(三角)と使用した場合(四角)についてデータを取得しています。各データにフィッティングするモデルとしてはマリュスの法則(実線)を用いました。2つの曲線間の位相シフト
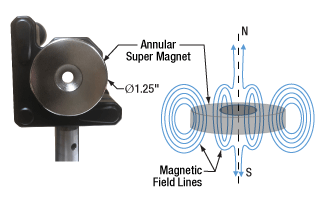
Click to Enlarge
図2: 試験する結晶は環状磁石(左)の穴の中に設置しました。長さ2.2 mmの結晶を長さ6.35 mmの穴の中心に設置しました。その位置で磁場は最も強くかつ均一になり、その方向はN-S軸に沿っています(右)。
| Curve Fit to Data Acquired Without Magnet | Curve Fit to Data Acquired With Magnet | Faraday Rotation (Δθ ) |
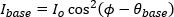 |  | 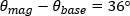 |
ファラデー回転
ファラデー効果による偏光状態の回転はファラデー回転と呼ばれ、その大きさは物質内の磁場の強度(B)と、磁場中に置かれた物質内を伝搬する光の光路長(L)の両方に正比例します。この比例定数はベルデ定数(V )と呼ばれます。
この物質固有のパラメータは波長と温度に依存し、その物質のファラデー効果の大きさを特徴づけるものです。ベルデ定数が既知の場合、磁場の強度と物質の長さを用いて、ファラデー回転(Δθ )は次の式で表されます。
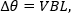
ベルデ定数を得る一つの方法として、特定の長さの物質と既知の磁場強度におけるファラデー回転を測定する方法があります。
ファラデー効果の測定
この方法に基づき、図1のセットアップを使用してCdMgTe結晶のファラデー効果の大きさを測定しました。
785 nmのファイバ出力型レーザからのコリメート光で構成された直線偏光光源からの出射光を、まず固定された直線偏光子に透過させました。
測定可能なファラデー回転を発生させるのに十分な磁場強度を得るために、環状の磁石を使用しました。結晶は、磁場が最も強い磁石の穴の中心に取り付けました(図2)。
結晶からの出射光は、目盛り付き回転マウントに固定された2つ目の直線偏光子を透過し、センサに到達します。パワーセンサは、直線偏光子の出射側にできるだけ近接して設置しました。
磁石を使用したセットアップと使用しないセットアップで測定を行いました。各データセット(図3)は、2番目の直線偏光子の透過軸の角度を2°刻みで変えて測定した平均パワーの記録です。2つの曲線は同じ周期で振動しますが、位相が互いにずれています
ベルデ定数の計算
図3の2つの曲線間の位相差がファラデー回転です。この値は、次のマリュスの法則を用いて各データをフィッティングさせた後に決定できます。
 ,
,
ここで、Ioは入射光の強度、 は2番目の直線偏光子の透過軸の角度です。フィッティングパラメータ(θ)は、各データセットで独立に最適化された定数です(それぞれ表内のθ base とθ mag )。2つのフィッティングパラメータの差がファラデー回転です(36°)。このファラデー回転の値を使用してベルデ定数を計算できます。
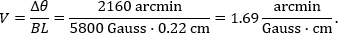
磁石の穴の中心での磁場強度(B) は5800ガウス、結晶の長さ(L)は0.22 cmで、ファラデー回転の角度(Δθ = 36°)は60の係数を掛けて2160 arcminに変換しています。
本コンテンツはZoya Shafique氏からご提供いただきました。
最終更新日:2021年1月14日
ファラデー回転の方向と回転角の大きさを求めるには何が必要か
ファラデー回転角の向きと大きさを決定するために、ここでは直線偏光の入射光と強度の調整が可能な磁場の両方を使用します。ファラデー回転はファラデー効果によって生じます。この効果によって、磁場中に置かれた物質内を直線偏光が伝搬していく過程で、その偏光方向が回転します。ファラデー回転角の特性は、物質から出射する光の偏光方向の磁場依存性を測定し、解析することで得られます。物質に入射する偏光の向きと物質から出射する偏光の向きの間の角度差を、それぞれの磁場強度で測定します。固定長のCdMgTe結晶を用いた例で示しているように、この一連の角度差の値を用いて特定の磁場強度におけるファラデー回転角を求めることができます。
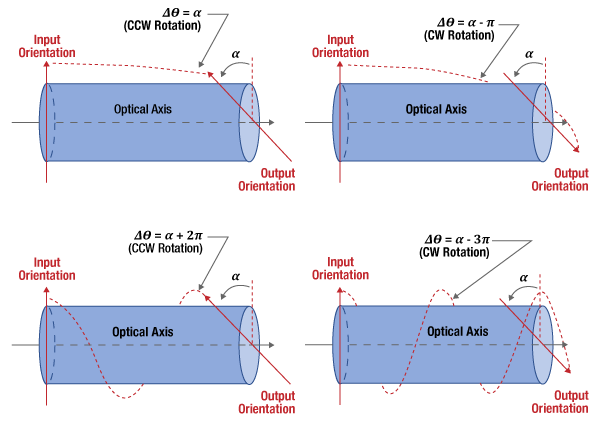
Click to Enlarge
図1:ファラデー効果により、直線偏光の偏光面は光軸周りで回転します。回転方向や回転数は、印加する磁場、光の伝搬方向、および物質の特性に依存します。ファラデー回転の方向と大きさ(Δθ )は、物質への入射光の偏光方向と出射光の偏光方向の間の角度(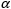 )を測定するだけでは決定できません。なぜならそれらの角度は0~
)を測定するだけでは決定できません。なぜならそれらの角度は0~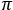 の間の値に割り当てられてしまうためです。
の間の値に割り当てられてしまうためです。
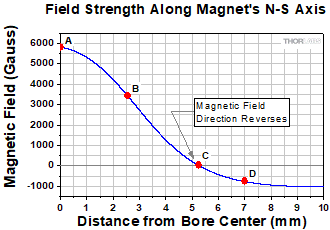
Click to Enlarge
図3:この作業で使用している環状磁石の穴を通る磁場の計算値です。グラフに示されている各点は図2の各点にそれぞれ対応しています。A点は穴の中心に位置し、C点での磁場はゼロです。磁場が磁石のS極に向いているとき、磁場の強度は正の値になります。
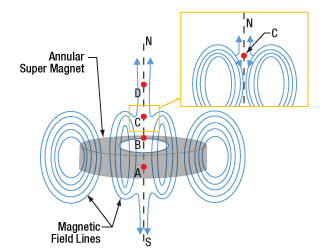
Click to Enlarge
図2:この作業に使用された環状磁石です。NS軸に沿った磁場(計算値)のモデルを図3に示します。上の図のA~Dにおける磁場の強度は、図3のグラフ上の対応する各点で見ることができます。C点において、磁力線は互いに相殺します。また、この点を境に磁場の方向も逆向きになります。
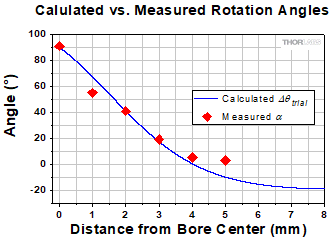
Click to Enlarge
図4:角度の計算値 (Δθtrial )と測定値 (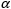 )を同じグラフ上に表示してみるのは、両者の関係性を可視化する1つの方法です。表に示すように、5800 Gaussの磁場を印加して測定された
)を同じグラフ上に表示してみるのは、両者の関係性を可視化する1つの方法です。表に示すように、5800 Gaussの磁場を印加して測定された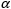 の値を用いて定数(Vtrial )を計算し、その結果を用いてΔθtrialを求めました。Δθtrialと測定値
の値を用いて定数(Vtrial )を計算し、その結果を用いてΔθtrialを求めました。Δθtrialと測定値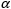 は良く一致しているため、測定された角度はファラデー回転角に等しいと言えます。
は良く一致しているため、測定された角度はファラデー回転角に等しいと言えます。
| Trial Verdet Constant Calculation (Vtrial ) |
 |
| Trial Faraday Rotation Calculation (Δθtrial ) |
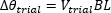 |
ファラデー回転角
光軸周りのファラデー回転の方向は、磁場
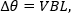
で与えられ、印加された磁場の影響下にある物質内の伝搬距離
測定された角度
物質に入射する直線偏光の向きと、物質から出射する直線偏光の向きを比較する方法 では、角度(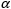 )が得られます。しかし、この方法では各角度が0~
)が得られます。しかし、この方法では各角度が0~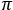 間の数値に自動的に割り当てられてしまい、光軸周りの直線偏光の回転方向と回転数を知ることはできません(図1)。
間の数値に自動的に割り当てられてしまい、光軸周りの直線偏光の回転方向と回転数を知ることはできません(図1)。
磁場の強度を変える
磁場を変えて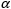 の値を測定すると、特定の磁場におけるファラデー回転角を求めることができます。時間的には一定で空間的には変化する磁場内で物質(試料)の位置を変えると、印加される磁場の強度は変化します。
の値を測定すると、特定の磁場におけるファラデー回転角を求めることができます。時間的には一定で空間的には変化する磁場内で物質(試料)の位置を変えると、印加される磁場の強度は変化します。
例えば、環状磁石の穴の中心軸(NS軸)上での軸に平行な磁場の強度は、その位置によって変化します(図2と3参照)。図3の磁場のグラフは、環状磁石のモデルをベースに計算されています。
磁場の強度は、磁場の向きを変えずに、試料をNS軸に沿って移動させることで変えることができます。この作業では、試料を軸に沿って特定の位置に移動させますが、その位置は磁石の穴の中心から測定しています。
ファラデー回転の特性
ファラデー回転角の特性を取得する便利な方法は、まず最初に、様々な磁場強度で測定される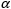 の値が、対応するファラデー回転角の大きさに一致すると仮定してみることです。そして、次のステップとして、その仮定をテストします。
の値が、対応するファラデー回転角の大きさに一致すると仮定してみることです。そして、次のステップとして、その仮定をテストします。
ここでは、長さ0.22 cmのCdMgTe結晶に磁場が印加されたときのファラデー回転角の方向と大きさを求めています。環状磁石によって磁場を発生させ、結晶をNS軸に沿って様々な位置に置いて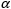 の値を測定しました。結晶は、まず図2に示すA点からC点まで移動しました。この範囲内では、光は磁場方向に沿って伝搬します。C点の通過後、磁場の方向は逆向きになります。
の値を測定しました。結晶は、まず図2に示すA点からC点まで移動しました。この範囲内では、光は磁場方向に沿って伝搬します。C点の通過後、磁場の方向は逆向きになります。
ベルデ定数の試行値(Vtrial、表参照)は、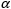 (2160 arcmin)の値と対応する磁場強度 (5800 Gauss)を用いて算出しました。ファラデー回転角の試行値(Δθtrial 、表参照)は、Vtrialを用いて算出しました。測定値とこのモデルによるデータが良く一致していることから(図4)、
(2160 arcmin)の値と対応する磁場強度 (5800 Gauss)を用いて算出しました。ファラデー回転角の試行値(Δθtrial 、表参照)は、Vtrialを用いて算出しました。測定値とこのモデルによるデータが良く一致していることから(図4)、 の測定値はファラデー回転角に等しいと言えます。角度の計算値と測定値の相違は、主にモデル化された磁場と実際の磁場との違いによるものですが、測定誤差が影響している可能性もあります。図4のグラフ化されたデータからは、計算されたベルデ定数の符号が正であること、また式に
の測定値はファラデー回転角に等しいと言えます。角度の計算値と測定値の相違は、主にモデル化された磁場と実際の磁場との違いによるものですが、測定誤差が影響している可能性もあります。図4のグラフ化されたデータからは、計算されたベルデ定数の符号が正であること、また式に を適用することでベルデ定数を正確に計算できることが分かります。
を適用することでベルデ定数を正確に計算できることが分かります。
この角度データの2つのセットが一致しない場合は、実際のファラデー回転角は測定された角度 と
と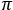 の倍数の和ということになります。特殊なケースとして、測定された角度
の倍数の和ということになります。特殊なケースとして、測定された角度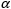 と、計算されたファラデー回転角の試行値の大きさは等しいけれど符号が反対である場合があります。このときの2つの角度の差は
と、計算されたファラデー回転角の試行値の大きさは等しいけれど符号が反対である場合があります。このときの2つの角度の差は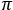 であり、実際のベルデ定数とベルデ定数の試行値の符号は反対になります。
であり、実際のベルデ定数とベルデ定数の試行値の符号は反対になります。
本コンテンツはZoya Shafique氏からご提供いただきました。
最終更新日:2021年5月20日
立ち上がり時間の波長依存性について
Click to Enlarge
図2: シリコン、ゲルマニウム、インジウムガリウムヒ素(In0.53Ga0.47As)の吸収係数と侵入深さ(典型値)のグラフです。侵入深さは吸収係数の逆数です。
Click to Enlarge
図 1:PN接合のディテクタへの光の平均侵入深さは波長によって異なります。侵入深さは吸収係数に関係しますが、その吸収係数は波長に依存します(図2)。
フォトダイオードに光が入射したとき、空気/半導体界面からのフレネル反射で反射されなった光子は、半導体材料内を伝搬していきます。
光子は、吸収されるか、あるいは最後の末端に到達するまで伝搬を続けます。光子が吸収された場合には、電荷担体のペアが生成されます。
空乏領域内で生成された電荷担体は、ほぼ即座に光電流に寄与することができます。しかし、空乏領域以外で生成された電荷担体の場合は、空乏領域まで移動するのに余分なステップを踏む必要があります。この移動に要する時間が拡散時間です。図1では、青色と赤色の光子がP型とN型の領域でそれぞれ電荷担体を生成しています。これらは空乏領域まで拡散しなければなりません。
半導体に入射した光子が吸収される確率は吸収係数に基づいて決まります。図2では、ディテクタに使用される様々な材料における、吸収係数と侵入深さの波長依存性を示しています。
入射光波長が長くなると、吸収係数が小さくなります。これは、より長波長の光子は、吸収されて電荷担体のペアを生成するまでに、平均的により長い距離を伝搬することを意味します。また、電荷担体が空乏領域に到達するまでの距離が長くなれば、立ち上がり時間も長くなります。
図3~5は、シリコン、InGaAs、およびゲルマニウムのフォトダイオードで測定された立ち上がり時間のグラフです。Siフォトダイオードのグラフでは、800 nm未満の波長域での傾斜はほぼ平坦です。これは、表面付近で吸収された光子の拡散時間は無視できることを示唆しています。800 nm以上では立ち上がり時間は急激に大きくなります。Siフォトダイオードの800 nmでの侵入深さは9 µm(図2)であるため、これはセンサの上部から空乏領域の底部までの距離が9 µmより小さいことを示唆しています。
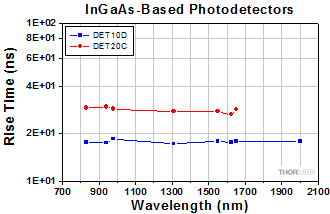
Click to Enlarge
図4: InGaAsフォトディテクタの立ち上がり時間
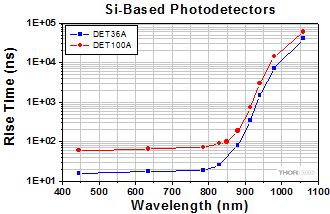
Click to Enlarge
図3: Siフォトディテクタの立ち上がり時間
最終更新日:2019年12月4日
1
Insights:偏波保持(PM)ファイバ
スクロールするか下のリンクをクリックすると、偏波保持ファイバの出射光についての解説をご覧いただけます。
- 偏波保持ファイバはすべての入射偏光状態を維持するか
- 偏波保持ファイバはどのようにして直線偏光を維持するのか
- PANDA型およびボウタイ型偏波保持ファイバからの出射光の消光比(ER)を制限する要因
- ビート長とは?ビート長が偏波消光比の代わりに偏波保持ファイバの仕様として明記されている理由
- ストレスロッド(応力付与ロッド)タイプの偏波保持ファイバの温度依存性
偏波保持ファイバはすべての入射偏光状態を維持するか
偏波保持(PM)ファイバは、ファイバの2つの直交軸のうちの1つに対して平行に偏光する直線偏光しか維持しません。偏波保持ファイバで直線偏光の方向が重要なのは、偏波保持ファイバの2つの直交軸の屈折率が異なるからです。屈折率が高い方向(スロー軸)に沿って偏光する光は、直交方向(ファスト軸)に沿って偏光する光よりも遅く進みます。
直線偏光として入射した光線が、これらの2つの軸のいずれかに平行な偏光でない場合、ファイバから出射する光は楕円偏光します。しかし楕円偏光状態はファイバ長に渡る温度と応力の変化に依存するため、予測ができず、かつ安定しません。
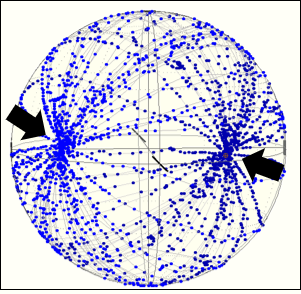
Click to Enlarge
図1:偏波保持ファイバーパッチケーブルの出射光を偏光計によりポアンカレ球表示。矢印で示されている点は、直線偏光とファイバ軸の1つが適切にアラインメントされている結果です。これらの入射状態はファイバによって維持されています。その他の点は楕円偏光状態を示し、入射偏光方向がファイバ軸の1つに平行ではないときの結果です。
偏波保持ファイバは光を偏光しない
偏波保持ファイバは直線偏光子のように作用せず、任意の入射偏光状態を直線偏光状態に変換する機能は有しておりません。
直線偏光子には2つの直交軸が規定されていますが、これらは偏波保持ファイバのスロー軸とファスト軸に相当するものではありません。直線偏光子の場合、軸の1つに対して平行に偏光する光は減衰し、もう1つの軸に対して平行に偏光する光が透過します。1つの偏光成分のみが透過するので、出射光は直線偏光となります。
偏波保持ファイバは直交する偏光成分のどちらも透過させ、どちらかを減衰させることはないため、直線偏光子としてはご使用いただけません。
波長板との比較
偏波保持ファイバと波長板にはどちらもファスト軸とスロー軸があるなど、多くの共通点があります。直線偏光の偏光軸がスロー軸またはファスト軸のどちらかに平行であるとき、偏波保持ファイバと波長板のどちらもその偏光状態を維持します。しかし、入射ビームにスロー軸とファスト軸の両方に沿って偏光する成分がある場合、偏波保持ファイバと波長板のどちらもその入射偏光状態を維持しません。
偏波保持ファイバと波長板は、スロー軸に平行な偏光成分をファスト軸に平行な偏光成分より遅らせることで、光の偏光状態を変化させます。しかし、偏波保持ファイバはファイバにかかる温度や応力の変化によりこの遅延が変動するため、波長板の代わりに使用することはできません。
出射偏光状態
図1で ポアンカレ球上に表示されている偏光計の測定結果は、偏波保持ファイバーパッチケーブルがもたらす様々な楕円偏光状態を示しています。これは直線偏光がファイバ軸に対して任意の方向に入射されているときに起こります。ファイバによりが入射偏光状態が維持されているとき、出射光の偏光計測定結果は、黒い矢印で示している2つの値の内の1つとなります。これらの値は、入射偏光状態の偏光方向とファイバ軸の1つの間のアライメントが適切である結果です。その他の点はすべて楕円偏光状態を示しており、これは入射偏光状態がどちらのファイバ軸に対しても平行ではないときに起こります。
図のデータの軌跡は、直線偏光の偏光方向を光軸の周りで1回転させて生成しました。軌跡がオーバーラップしないのは、ファイバの温度が毎回、回転後に変化したからです。ファイバの温度の感度により、温度が変化する度に異なる楕円偏光状態を得ます。なお、各軌跡が黒矢印の点を通過することをご確認ください。これは入射時の直線偏光状態がファイバ軸の1つによくアライメントされているとき、出射時の偏光状態が温度や応力の変化に依存しないことを示しています。
最終更新日:2020年8月6日
偏波保持ファイバはどのようにして直線偏光を維持するのか
偏波保持(PM)ファイバでは直交する「スロー軸」と「ファスト軸」の間の屈折率の差(複屈折性)が著しく、この複屈折性により偏波保持ファイバが入射光の偏光状態を維持することができます。しかし、入射偏光状態は、2つのファイバ軸のうちの1つに平行にアライメントされていなければ維持することはできません。
偏波保持ファイバはその複屈折性により、ファイバのスロー軸とファスト軸で速度差、より正確に言えば伝搬定数差があり、偏光を保持するためにはスロー軸・ファスト軸に対して平行な偏光とする必要があります。光が直交偏光に切り替わるためには、光の速度(伝搬定数)も直交軸の条件に合う必要が出てきます。ファイバの複屈折を小さくしないと、このような速度変化は起きにくくなります。このようにして、複屈折を有するファイバでは、偏光が維持されます。
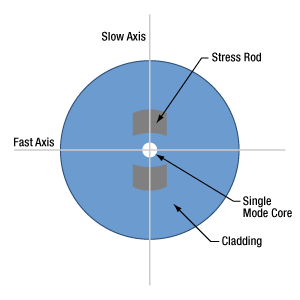
Click to Enlarge
図 3:ボウタイ型ファイバでは、2本のウェッジ型ストレスロッドを使用してコアで張力を得て、複屈折にしています。スロー軸に沿った応力は、製造後のファイバが冷却されていくにつれ、ストレスロッドがクラッドよりも収縮するために付与されます。
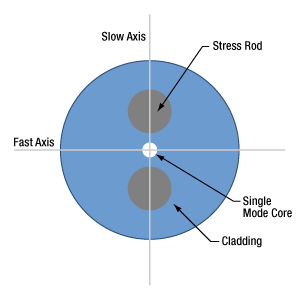
Click to Enlarge
図2:PANDA型偏波保持ファイバは、2本の円柱型ストレスロッドを使用してコアで張力を得て、複屈折にしています。スロー軸に沿った応力は、製造後のファイバが冷却されていくにつれ、ストレスロッドがクラッドよりも収縮するために付与されます。
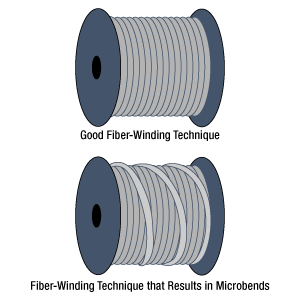
Click to Enlarge
図 4:マイクロベンドを最小化するにはきれいに緩く巻き付けてください(上)。マイクロベンドは、巻き付けたファイバによる凸凹面を横切って巻き付けることにより生じます(下)。
応力の効果について
偏波保持ファイバを構築する方法の1つにファイバーコアに機械的な応力を付与する方法があります。応力によりガラスに複屈折(光弾性)が生じるからです。このように応力を利用した複屈折ファイバで最も一般的なのはPANDA型とボウタイ型で、ファイバのコアに張力が加えられています。
これらの製品では、ストレスロッドと呼ばれるガラスの構造がファイバの全長に渡り、ファイバのコアに平行に伸びています。図2と3の断面図で見ると、ストレスロッドとファイバのコアは直線状に配置されています。製造後のファイバが冷却されていくにつれ、ストレスロッド内のガラスは、周りのクラッド内のガラスよりも収縮されます。ストレスロッドの収縮からの引っ張りにより、コアでは張力が生じ(スロー軸)、直交方向(ファスト軸)にはコアよりも小さい応力がかかります。そのため2つの軸では屈折率差が生じます。
応力低下ともたらす影響について
応力複屈折ファイバのコアでの張力は、温度に依存します。これは、ストレスロッドのガラスとクラッドのガラスで熱膨張率(CTE)が異なるからです。ストレスロッドによりもたらされる張力は、動作温度が高くなると低くなります。これにより複屈折率、そして偏光を維持するファイバの性能が低下するため、結果、消光比(ER)が低下する場合があります。
コアでの張力は、ファイバを小さく巻きつけたり、急激に曲げたり、あるいは凸凹の面に固定するなど、取扱い方によって生じる応力によっても低下する場合があります。局所的な応力付与部におけるマイクロベンドが直交偏光に散乱光を入射し、消光比が低下します。マイクロベンドはファイバの不適切な巻き付け方(図4)、あるいはファイバ素線を表面に押し付けることによって起こる場合があります。
一般的にファイバーコネクタは消光比を低下させます。それは、ファイバを固定するために硬化した樹脂化合物が非対称性の応力の原因となったり、化合物内の樹脂泡がファイバに圧力をかけたり、またファイバとフェルールの内孔が接触し圧力が加わる場合があるからです。一般的に各メーカはファイバの消光比を最大化するために、これらの応力を抑える手段をとっていますが、これらの応力は完全に除去することはできません。
形状複屈折ファイバ
応力複屈折ファイバの温度依存性が好ましくないときには、温度に依存性のない形状複屈折ファイバがございます。これらの偏波保持ファイバの複屈折性は、ストレスロッドによる張力ではなく、楕円形のコアにより生じます(図5)。
偏波保持フォトニック結晶ファイバを含む形状複屈折ファイバは、すべての用途に適しているわけではありません。楕円形のコアと減衰量、そして小さなモードサイズは通信用途には適しませんが、ファイバーセンサでよく使用されています。
参考文献
[1] Chris Emslie, in Specialty Optical Fibers Handbook, edited by Alexis Mendez and T. F. Morse (Elsevier, Inc., New York, 2007) pp. 243-277.
[2] Malcolm P. Varnham et al., "Analytic Solution for the Birefringence Produced by Thermal Stress in Polarization-Maintaining Optical Fibers," J. Lightwave Technol., LT-1(2), 332-339 (1983).
[3] Zhenyang Ding et al., "Accurate Method for Measuring the Thermal Coefficient of Group Birefringence of Polarization-Maintaining Fibers," Opt. Lett., 36(11), 2173-2175 (2011).
[4] M. Shah Alam and Sarkar Rahat M. Anwar, "Modal Propagation Properties of Elliptical Core Optical Fibers Considering Stress-Optic Effects," World Academy of Science, Engineering and Technology, Open Science Index 44, International Journal of Electronics and Communication Engineering, 4(8), 1170 - 1175 (2010).
最終更新日:2020年9月11日
PANDA型およびボウタイ型偏波保持ファイバからの出射光の消光比(ER)を制限する要因
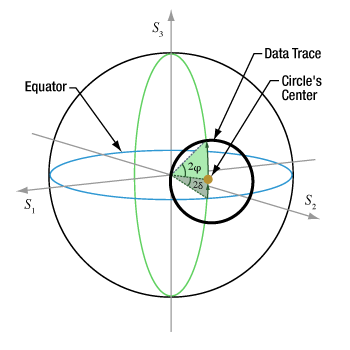
Click to Enlarge
図 6:クロストークの影響により、偏波保持ファイバは一般的にやや楕円形状の偏光を出射します。偏波保持ファイバの温度を変えることで、出射する楕円偏光の状態を制御することができます。偏光の測定値はポアンカレ球上で円の軌跡をたどり、出射光の特性化に使用することができます。
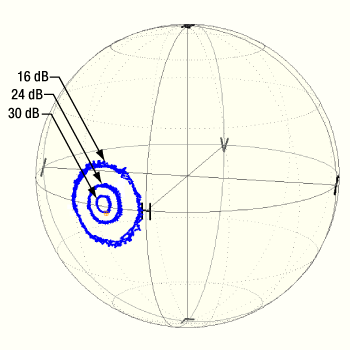
Click to Enlarge
図 7:3つの異なるデータの軌跡がポアンカレ球にプロットされています。いずれも入射偏光状態と偏波保持ファイバ軸の間の角度の不一致を示しています。軌跡はヒートガンを用いてファイバの温度を変化させ、出射偏光状態を回転させることで取得しました。角度の不一致度が減少するにつれ、温度に依存する偏光状態の範囲が小さくなり、消光比が増加します。各軌跡の消光比はdBで表されています。
PANDA型およびボウタイ型の偏波保持ファイバは、不適切なファイバへの光入力結合、ファイバにかかる外部応力の影響、あるいは不完全な状態のファイバの作用により、出射光の消光比(ER)が入射光と比べて低くなる場合があります。光の一部が直交偏光状態に変換されると、消光比は低下します。
ミスアライメントによるクロストーク量の概算
クロストーク(クロスカップリング)は、光の一部が直交方向に対して平行に偏光すると生じます。偏波保持ファイバへの光の結合は、光源とファイバの偏光軸間でミスアライメント(回転)があるとクロストークをもたらします。このとき、光源からの直線偏光がファイバのスロー軸とファスト軸によって別々に誘導される2つの直交する偏光成分の間で分岐されます。
ミスアライメントによるクロストーク量は大きく、出射偏光を測定中にファイバの温度を変化させることで概算することができます。出射光に直交する両方の偏光成分が含まれる場合、その成分の間の遅延は温度によって変動します。温度の変化に応じて出射光の楕円偏光が変化します。
温度の依存する偏光の測定値をポアンカレ球にプロットすると、その軌跡は円になります(図6と7)。ミスアライメントによるクロストーク量の概算値は、図6における角度(2φ)から求められます。
2φは楕円化の具合を表しています。半角(φ )をラジアンで表すと、クロストークの概算量(dB)は、下記の式で求められます。
Cross Talk (dB) ≈ -20 log (tan(φ )).
光源とファイバ間のアライメントを改善する方法の1つは、温度に依存するファイバの出射偏光状態の変動が最小限に抑えられるところまで、光源の偏光角度を光軸周りで回転調整することです。
出射光の消光比の概算
ファイバを伝搬する光は、不完全な状態のファイバであってもクロストーク量は小さいですが、外部からの応力の影響により消光比は著しく低下する場合があります。ファイバを小さく、あるいは凸凹面や鋭角な面にきつく巻き付けたり、ファイバ素線を固い面に固定したりすることも消光比を低下させます。ファイバーコネクタも、ファイバ素線、コネクタのフェルール、あるいは樹脂化合物との接触による応力によりクロストークの大きな原因となる場合があります。
消光比(ER)の概算値は様々な式で求めることができます。
ERδ (dB) ≈ -20 log (tan(φ + |δ |)).
上記の1つ目の式は、ミスアライメントによるクロストーク量の求め方と似ていますが、不完全な状態のファイバによるクロストーク、マイクロベンド、その他ファイバの長さ方向に渡り付与される影響が含まれています。これらの影響により、円の軌跡の中心がポアンカレ球の赤道から2δ角度分だけ変位します。
| with |
|
上記はより確度の高い式で、偏光強度を合計の強度を割った偏光度(DOP)が含まれています。
参考文献
[1] Chris Emslie, in Specialty Optical Fibers Handbook, edited by Alexis Mendez and T. F. Morse (Elsevier, Inc., New York, 2007) pp. 243-277.
[2] Edward Collett, Polarized Light in Fiber Optics (Elsevier, Inc., New York, 2007) pp. 45-53.
最終更新日:2020年9月11日
ビート長とは?ビート長が偏波消光比の代わりに偏波保持ファイバの仕様として明記されている理由
偏波保持(PM)ファイバの出射光の偏波消光比(PER)は、ファイバ製造メーカにとって明記することが難しい仕様です。その理由は、このパラメータがファイバ長、入射光の状態、偏光、アライメントに依存するからです。ビート長はこれらの要素に依存しないため、偏波保持ファイバのポテンシャルを数値化するのに便利なパラメータです。ビート長は短いほどよく、偏波保持ファイバとその動作温度を選択するうえで参照できる有用なパラメータです。ビート長により偏波保持ファイバのポテンシャルに関する情報が得られますが、実際の性能とファイバの出射光のPERは、最終的にファイバの配置に依存します。
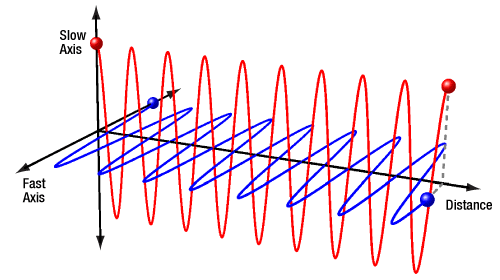
Click to Enlarge
図1:赤と青の曲線はそれぞれ偏波保持ファイバのスロー軸とファスト軸に対して平行に偏光する波形を表しています。スロー軸の方が屈折率が大きいため、この軸に対して平行に偏光する波(赤)の方がより速いレートで振動します。これは(球によって示される)波の振幅を2つの異なる位置から見ることで確認できます。
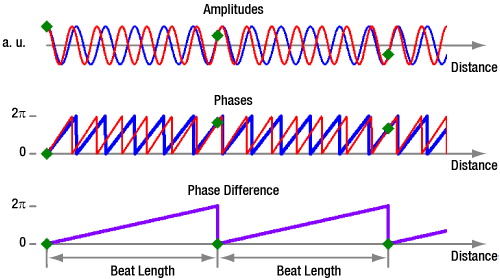
Click to Enlarge
図2:図1で示された波形の振幅を横軸を伝搬距離としてプロットされています(上図)。なお、この図の距離は図1よりも長いことにご留意ください。各波形の位相は0~2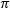 の範囲でプロットされていますが(中央の図)、これらは2
の範囲でプロットされていますが(中央の図)、これらは2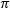 で折り返されて表示されているため、実際の絶対位相はリニアに大きくなります。波形の位相差(下図、
で折り返されて表示されているため、実際の絶対位相はリニアに大きくなります。波形の位相差(下図、  の範囲でプロット)は、距離とともに直線的に増加します。
の範囲でプロット)は、距離とともに直線的に増加します。
3つのグラフの緑色の菱形マークは、0~2 のスケールで両方の波形が同じ位相であるポイントを示しています。マークとマークの間では、スロー軸の波形がファスト軸の波形に比べて2
のスケールで両方の波形が同じ位相であるポイントを示しています。マークとマークの間では、スロー軸の波形がファスト軸の波形に比べて2 余分に位相を蓄積しています。なお、一般的にこの位相は周期の整数で得られるものではありません。ビート長は、この蓄積された位相差が2
余分に位相を蓄積しています。なお、一般的にこの位相は周期の整数で得られるものではありません。ビート長は、この蓄積された位相差が2 となる距離のことで、これは菱形マークとマークの間の距離でもあります。
となる距離のことで、これは菱形マークとマークの間の距離でもあります。
偏波保持ファイバのビート長
偏波保持ファイバのビート長は、ファイバの2つの直交軸であるファスト軸とスロー軸に沿って伝搬する波を比較することで分かります。ファイバ内でこれらの波形が励起するには、単色の直線偏光を入射させ、入射光の偏光角をファイバのファスト軸とスロー軸との中間にします。
これにより直交する偏光波は、同じ振幅を持ち、同位相でファイバに入射されます。しかし波形は伝搬するにつれて同位相を保たなくなります。これはスロー軸の屈折率がファスト軸よりも大きいからです
2つの波形の位相差は伝搬距離とともに直線的に増加します(図2)。2つの波形の位相差が
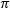
ビート長(Lp )
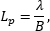
は波長(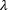 )に比例し、ファイバの複屈折率差
)に比例し、ファイバの複屈折率差
ビート長の典型値について
2つのファイバ軸の間の屈折率差が大きければ大きいほど、複屈折は大きく、ビート長は短く、そしてファイバの偏光保持性能は高くなります。ビート長は、ファイバの複屈折性に変化がない限り、ファイバ長に沿って一定です。製造メーカーはよくいくつかの波長に対するビート長と温度の制限範囲を仕様に明記しています。
以前は、ビート長が1 mm未満の偏波保持ファイバは、楕円のコアで、かつ、標準的なシングルモードファイバに比べて著しく小さいモードフィールド径を持ちました。しかし、多くの用途では、円状のコアと標準的なシングルモードファイバに近いモードフィールド径を持つファイバが必要とされます。これらの基準を満たし、性能の良い偏波保持ファイバのビート長は1 mm~数ミリの間となります。標準的なシングルモードファイバにも測定可能なビート長がありますが、それはメートル単位の長さとなります。これは、コアが完全な円状の断面にはなっていないことに起因しています。コアの楕円率はわずかで、ファイバ長に沿ってランダムに変化するため、標準的なシングルモードファイバは、偏波保持ファイバとしては有用ではありません。
ビートパターン
偏波保持ファイバの場合、ビート長が示すのは、偏波保持ファイバの直交するスロー軸とファスト軸に平行に偏光する波の間で繰り返し示される位相の関係となります。ファイバの任意の位置での位相差が、その光の偏光状態を決定します。例えば同位相であれば光は直線偏光で、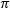 /2 (90°)の差があれば円偏光です。
/2 (90°)の差があれば円偏光です。
これらの波は互いに直交して偏光するため、振幅のビートパターンは生じません。振幅のビートパターンが生じるのは、2つの波に互いに平行に偏光する成分を持つときのみです。同じ理由により、フォトディテクタを使用して周期の異なる2つの直交して偏光する波を合わせた強度を測定するとき、干渉成分がゼロに等しい信号を得ます。
参考文献
[1] Chris Emslie, in Specialty Optical Fibers Handbook, edited by Alexis Mendez and T. F. Morse (Elsevier, Inc., New York, 2007) pp. 243-277.
[2] Malcolm P. Varnham et al., "Analytic Solution for the Birefringence Produced by Thermal Stress in Polarization-Maintaining Optical Fibers," J. Lightwave Technol., LT-1(2), 332-339 (1983).
最終更新日:2021年7月30日
Content improved by our readers!
ストレスロッド(応力付与ロッド)タイプの偏波保持ファイバの温度依存性

Click to Enlarge
図9:パンダ型の偏波保持ファイバにはクラッドにストレスロッド(応力付与ロッド)が存在します。これらの円筒径のロッドは、コアに対して平行に配置されています。ファイバの温度が加工時の温度より下がるにつれ、ストレスロッドのガラスは周りのクラッドよりも収縮するため、コアがスロー軸に沿って引っ張られます。
| Source of Change in Delay | Change in Parameter | Resulting Change in Delay | |
| Birefringence | Length | ||
Birefringence | | --- | |
Fiber Length | --- | 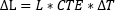 | 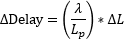 |
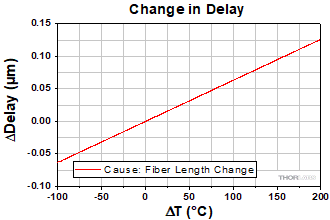
Click to Enlarge
図 11:図10では、複屈折性の温度による変化のみが大きな影響があったため、図10の赤線のみをここに示しています。これらの値は、温度の変化によってファイバ長が増加し、ファイバの複屈折性が一定であることを仮定して計算されています。
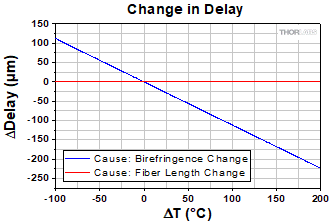
Click to Enlarge
図10:パンダ型偏波保持ファイバを伝搬する直交の偏光成分の間の相対遅延(y軸)は、ファイバの温度が変化すると変動(x軸)します。温度が上昇すると、偏波保持性能は低下します。性能は温度が下がることで向上します。青線と赤線の数値は、それぞれ複屈折性とファイバ長のみが温度によって変化することを仮定して計算されています。
偏波保持ファイバの直交するスロー軸とファスト軸の間の屈折率の差が大きければ大きいほど、偏波保持性能は良くなります。しかし、温度が上昇するにつれてコアの張力が下がるため、この差(複屈折性)は減少します。ファイバの複屈折性の減少は、温度の上昇にほぼ比例します。
温度依存の複屈折性
パンダファイバやボウタイ型ファイバなどの応力複屈折の偏波保持ファイバは、クラッドにストレスロッド(応力付与ロッド)が存在します(図9)。ストレスロッドのガラスはクラッドのグラスよりも熱膨張係数(CTE)が高いため、加工後すぐにファイバの温度が下がるにつれて、ストレスロッドのガラスは周りのクラッドに比べて収縮速度が速くなります。より収縮するストレスロッドは、周りのクラッドを引っ張り、室温程度ではコアに大きな張力を与えます。これによりファイバのコアでは複屈折性が生じます。
比例定数(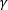 ) において、下記の複屈折性(B )の式は
) において、下記の複屈折性(B )の式は
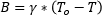 ,
,
ガラスの温度差の関係式で、温度差は液状からガラス状に変化するときの温度(
温度の影響の概算
偏波保持ファイバを伝搬するすべての光が同じファイバ軸に対して平行に偏光する場合、ファイバから出射する光の偏光状態は温度に依存しません。光に2つのファイバ軸に平行な偏光成分が含まれている場合、動作温度の変化により楕円偏光状態が変化します。
これは出射偏光状態を決定する2つの直交成分の間の相対遅延によるものです。遅延はファイバの複屈折性とファイバ長に依存しますが、このどちらも温度に依存性があります。しかし、ファイバの偏波保持性能に大きな影響を与えるのは複屈折性の変化のみです。
これら2つの出射偏光状態への影響は、表の式を使用して求めました。動作波長は1550 nm、ファイバはパンダ型ファイバ(PM980-XP)で長さ2 m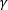 係数は
係数は
計算結果は図10と11のグラフに示しています。遅延(y軸)は温度の変化(x軸)によって変動します。これは、温度に依存する遅延をモニタすることで、温度に依存するファイバの複屈折性と、ファイバが偏光を維持するポテンシャルについての情報が得られることを示しています。
温度とビート長
ファイバの複屈折性が偏波保持ファイバの偏光維持力を決定しますが、複屈折性は通常製造メーカーによって明記されません。 ビート長は通常明記されているパラメータです。ビート長
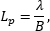
は波長( )と複屈折性の割合で、性能が高い偏波保持ほど短くなります。なお応力複屈折の偏波保持ファイバでは、ビート長は温度上昇とともに長くなります。
)と複屈折性の割合で、性能が高い偏波保持ほど短くなります。なお応力複屈折の偏波保持ファイバでは、ビート長は温度上昇とともに長くなります。
参考文献
[1] Chris Emslie, in Specialty Optical Fibers Handbook, edited by Alexis Mendez and T. F. Morse (Elsevier, Inc., New York, 2007) pp. 243-277.
[2] Malcolm P. Varnham et al., "Analytic Solution for the Birefringence Produced by Thermal Stress in Polarization-Maintaining Optical Fibers," J. Lightwave Technol., LT-1(2), 332-339 (1983).
[3] Zhenyang Ding et al., "Accurate Method for Measuring the Thermal Coefficient of Group Birefringence of Polarization-Maintaining Fibers," Opt. Lett., 36(11), 2173-2175 (2011).
[4] M. Cavillon, P. D. Dragic, and J. Ballato, "Additivity of the coefficient of thermal expansion in silicate optical fibers," Opt. Lett, 42(18), 3650 - 3653 (2017).
最終更新日:2020年9月16日
Insights:偏光
スクロールするか下のリンクをクリックして偏光に用いられるラベルと偏光楕円に対する偏光状態の影響についてご覧ください。
- 垂直成分と平行成分の識別に使用されるラベルについて
- 偏光楕円と偏光状態の関係
- 偏光状態を表すのにポアンカレ球が役に立つ理由
- 非偏光の光源を使用して偏光成分の消光比を測定する方法
- 直線偏光の光源を使用して偏光子の消光比を測定する方法
垂直成分と平行成分の識別に使用されるラベルについて
| Labels | Notes | |
|---|---|---|
| Perpendicular | Parallel | |
| s | p | Senkrecht (s) is 'perpendicular' in German. Parallel begins with 'p.' |
| TE | TM | TE: Transverse electric field. |
| ⊥ | // | ⊥ and // are symbols for perpendicular and parallel, respectively. |
| σ | π | The Greek letters corresponding to s and p are σ and π, respectively. |
| Sagittal | Tangential | A sagittal plane is a longitudinal plane that divides a body. |
図1:偏光は2つの成分のベクトルの和として説明されます。その成分の1つは、入射面と平行な電界振動面、もう一つは入射面と垂直な電界振動面です。なお、電界はビームの伝搬方向に対しても直交に振動します。
偏光が面に対して入射されるときには、よく垂直成分と平行成分で説明されます。これらの成分は互いに、そして光の伝搬方向に対して直交します(図1)。
垂直成分と平行成分に用いられるラベルや記号は、どちらがどちらだか分からなくなる場合があります。表では垂直成分と平行成分に使用されているラベルの一覧がご覧いただけます。
垂直ならびに平行方向は入射面を基準にして定義されています。図1の動画ではビームが表面から反射されている図で説明しています。入射面は、入射光と反射光の両方を含む面として定義されます。垂直方向は入射面に対して垂直、平行方向は入射面内に平行です。
垂直成分ならびに平行成分の電界は互いに直交する面で振動します。垂直成分の電界は入射面に対して垂直な面で、平行成分の電界は入射面内に平行な面で振動します。偏光は垂直成分と平行成分のベクトルの和です。
垂直入射光
垂直入射光の場合、入射面の定義できないため、このアプローチから光の垂直成分と平行成分を明確に定義することはできません。垂直入射光においてこれらを区別する必要性は限られています。なぜなら垂直入射光のすべての成分の反射率は同じだからです。
最終更新日:2020年3月5日
1
偏光楕円と偏光状態の関係
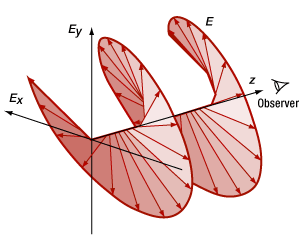
Click to Enlarge
図 3:電場( )が伝搬するとき、ベクトルの先端はらせんの軌道をたどります。この場合、伝搬は z軸に沿っており、
)が伝搬するとき、ベクトルの先端はらせんの軌道をたどります。この場合、伝搬は z軸に沿っており、 ベクトルはプラス(時計周り)のらせん軌道をたどります。
ベクトルはプラス(時計周り)のらせん軌道をたどります。
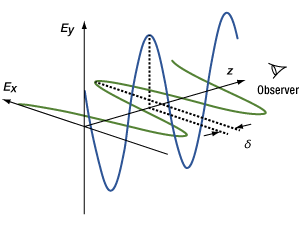
Click to Enlarge
図2:電場(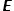 )は2つの直交成分(ExとEy )の和とその2つの位相差
)は2つの直交成分(ExとEy )の和とその2つの位相差
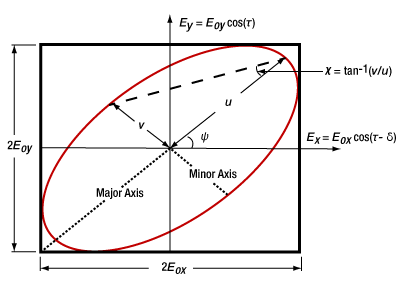
Click to Enlarge
図 4:観察者が図3の起点から伝搬しているビームを見ている場合、回転する電場ベクトルの先端は楕円を描いています。この楕円は角度Ψとχで表すことができます。この図で式(  /λ - ωt )は(
/λ - ωt )は( )により表されています。ここでλは波長、ωは角周波数、そしてtは時間です。
)により表されています。ここでλは波長、ωは角周波数、そしてtは時間です。
偏光楕円は偏光状態を可視化する方法の1つです。
レーザービームが伝搬するとき、電場ベクトルの先端は偏光状態によって決定する3次元の軌道に沿って移動します。光軸方向に垂直な断面への射影を見ると、ベクトルの先端が2次元の楕円軌道をたどりながら伝搬軸の周りを回転しているように見えます。
この軌道の形が偏光楕円です。この軌道は直線偏光では直線、円偏光では円になります。
光の成分
電場ベクトル(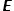 )は、その直交成分Ex とEy で表すことができます。図2では直線偏光でも円偏光でもない偏光楕円を図解しています。ExおよびEyの直交成分は異なる振幅を持っており、ExとEy 間の位相差(δ )は
)は、その直交成分Ex とEy で表すことができます。図2では直線偏光でも円偏光でもない偏光楕円を図解しています。ExおよびEyの直交成分は異なる振幅を持っており、ExとEy 間の位相差(δ )は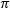 /2の整数倍ではありません。ExとEy の値は周期的に増加したり減少したりしますが、同期せずに変動し、その範囲は異なります。
/2の整数倍ではありません。ExとEy の値は周期的に増加したり減少したりしますが、同期せずに変動し、その範囲は異なります。
電場ベクトルは移動するとき伝搬軸の周りを回転し(図3)、その長さは回転角度によって異なります。Ex - Eyの伝搬軸に垂直な断面への射影を見るとき、ベクトルの先端は偏光楕円の曲線を描きます(図4)。
偏光楕円
観察者側から見るビームは、反対方向から見るのとは異なった偏光楕円となります。このため、観察者がどの方向から見ているのか特定する必要があります。ここでは観察者側から見ているビームを想定しています。
偏光楕円は長辺と短辺がEoxとEoy のそれぞれの振幅ExとEyの2倍に等しい長方形で囲われています。この長方形ではそれぞれの直交成分に含まれた光の割合についての情報が得られます。
偏光状態に応じた特定の偏光楕円の特徴を決定するには、Ex とEy の位相遅延も考慮する必要があります。偏光状態の情報を表している楕円における重要なパラメータはEx軸に対する長軸の角度と、長軸と短軸の長さの比になります。
楕円の長軸とEx軸の間の角度(ψ )、方位角、傾斜角、回転角、傾き角、アジマス角を含め多くの名称で呼ばれています。-90°から90°の間で変動し、EoxとEoyが等しいときには±45°となります。
偏光楕円の楕円率は、長軸と短軸の長さの比率(ε )です。方位は一般的に角度で表されるため、楕円率も角度( χ )表すと便利です。楕円率は、直線偏光のゼロ( χ = 0°)、この場合はδ = 0、から円偏光の1( χ = 45°)、この場合はδ = 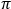 /2、までの値を取ります。
/2、までの値を取ります。
電場ベクトルの先端は、伝搬するときに右回り(時計回り)または左回り(反時計回り)に回転します。これは光のらせん性、ヘリシティとして知られており、右回りの偏光は正のヘリシティ、左回りの偏光は負のヘリシティを持ちます。方向は、時間がゼロのとき(Et=0 )のEベクトルの値と、(T )の1/4遅い時間(Et=T/4 )のEベクトルの値を使用して求めることができます。クロス積(
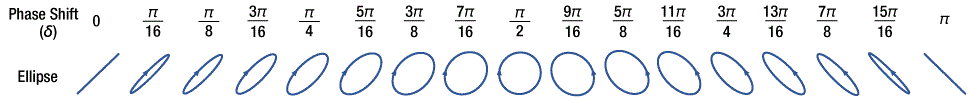
Click for Details
図5:偏光楕円の楕円率と方位角により、電場の直交成分ExとEyの位相差(δ )の情報が分かります。上記の楕円は両成分のピークの振幅が等しい場合を示しています。Eベクトルの回転方向は、偏光楕円の矢印で示されています。それぞれの楕円率と方位角についてがご覧いただけます。
最終更新日:2020年7月7日
偏光状態を表すのにポアンカレ球が役に立つ理由
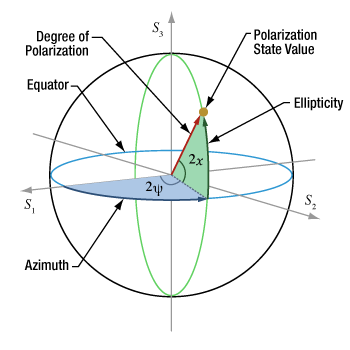
Click to Enlarge
図 5:偏光状態が方位角(S1軸基準)と楕円率(赤道基準)を用いてポアンカレ球にマッピングされています。偏光状態の半径は、光が完全な偏光のとき(無偏光が含まれていない)に最大値となります。
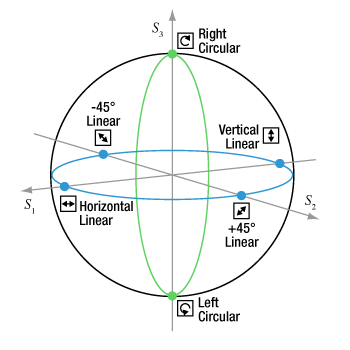
Click to Enlarge
図 6:球面の赤道(青線)上にマッピングされた偏光状態(青い円)は、完全な直線偏光です。S3軸上で±1の値でマッピングされた偏光状態(緑の円)は、円偏光です。直線でも円偏光でもない偏光楕円状態は球体のその他の領域でマッピングされています。
ポアンカレ球には、経緯と緯度を利用して地球儀上の位置を特定するのと同じように偏光状態がマッピングされます。ポアンカレ球での座標は2つの角度(方位角、楕円率)と半径を使用して特定されます。方位角と楕円率のパラメータは、偏光状態を表す偏光楕円からとります。半径は光の偏光度から求められます。最大値は完全な偏光に相当する1です。
ポアンカレ球と偏光楕円はどちらも偏光状態の可視化と偏光の観察に役立ちます。しかしポアンカレ球の大きな利点は、偏光状態の変化の計算が簡素化されることです。
ポアンカレ球のデータポイント
方位角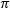 /2
/2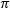 /4
/4
半径1は、球面に相当し、光が完全に偏光していることを示します。半径は無偏光の割合が増えると、小さくなります。偏光度(DOP)は、偏光強度を合計の強度で割った値です。
偏光状態のストークスパラメータ(S1、S2、S3)は偏光状態のデカルト座標に相当します(下表をご覧ください)。
2つの偏光状態の計算方法
ポアンカレ球面上にプロットされた2つの偏光状態を1本の弧でつなぎ、球面三角法を用いてそれぞれの方位角および楕円率の差を計算することができます。これは偏光素子と相互作用した後の光の偏光状態を予測したり、任意の偏光状態を得るために偏光素子が与えるべき方位角と楕円率を決定するのに便利な方法です。
| Cartesian to Poincaré Sphere Coordinates | |||
| S1 = cos(2χ)*cos(2ψ) | |||
| S2 = cos(2χ)sin(2ψ) | |||
| S3 = sin(2χ) | |||
| Selected Polarization States | Azimuth/2a | Ellipticity/2a | (S1, S2, S3) |
| Horizontal Linear | ψ = 0 | χ = 0 | (1, 0, 0) |
| +45° Linear | ψ = /4 /4 | χ = 0 | (0, 1, 0) |
| Vertical Linear | ψ =  /2 /2 | χ = 0 | (-1, 0, 0) |
| -45° Linear | ψ = 3 /4 /4 | χ = 0 | (0, -1, 0) |
| Right Circular | ψ = 0 | χ =  /4 /4 | (0, 0, 1) |
| Left Circular | ψ = 0 | χ = -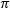 /4 /4 | (0, 0, -1) |
参考文献
[1] Edward Collett, Polarized Light in Fiber Optics (Elsevier, Inc., New York, 2007) pp. 45-53.
[2] Russell A. Chipman, Wai-Sze Tiffany Lam, and Garam Young, Polarized Light and Optical Systems (CRC Press, New York, 2019) pp. 80-83.
最終更新日:2020年9月11日
非偏光の光源を使用して偏光成分の消光比を測定する方法
試験対象の光学素子(DUT) の偏光消光比は、非偏光光源と光パワーセンサの間に高い消光比を有する参照用偏光子とDUTを配置することで推定することができます。この方法では参照用偏光子とDUTのペアを透過する最大パワーと最小パワーを測定します。参照用偏光子の消光比がDUTの消光比よりも非常に大きい場合には、この2つのパワーの測定値の比がDUTの消光比の正確な推定値を与えます。参照用偏光子とDUTが同じタイプの直線偏光子の場合(すなわち消光比が同様の場合)は、この方法では実際の消光比の約50%の値になります。参照用偏光子の消光比がDUTの消光比より2桁大きい場合は、この推定値はDUTの消光比の約99%になると予想されます。
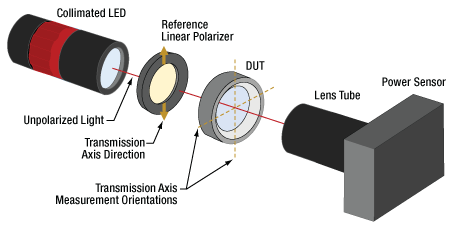
Click to Enlarge
図 8: 試験対象の光学素子(DUT)の消光比は、上図のようなセットアップを使用して測定できます。非偏光の光をLEDで発生させ、DUTと参照用直線偏光子を光源とパワーセンサの間に設置します。パワーセンサに取り付けられたレンズチューブは、パワーセンサからの迷光をブロックします。説明の都合上、参照用偏光子は固定されており、その透過軸は鉛直方向に向けられています。Pmax は、DUTと参照用偏光子の透過軸が平行(どちらも鉛直方向)のときに得られます。Pmin は、DUTと参照用偏光子の透過軸が垂直(すなわちDUTの透過軸が水平方向)のときに得られます。金色の点線は、この2つの測定に対応するDUTの2つの透過軸方向を示しています。
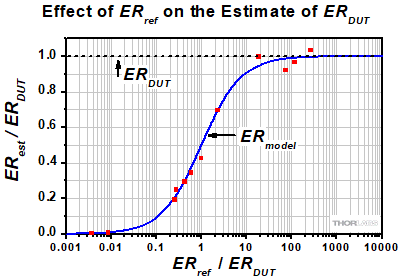
Click to Enlarge
図9: DUTの消光比の測定値
DUTの消光比の推定
図8の実験セットアップを使用してDUTの消光比(ERDUT )を推定できます。非偏光の光は、消光比(ERref )がすでに分かっている参照用偏光子を透過します。DUTを透過した光はディテクタで検出されます。
ERDUT の推定値は、2つの光パワーの測定値から計算できます。1つ目の測定値は参照用偏光子とDUTの透過軸が垂直のときに取得されます。透過軸が直交することで透過光パワーは最小値
2つ目の測定値は、2つの偏光子の透過軸が平行になったときに取得されます。このときセンサに到達する透過光パワーは最大値
Pmax とPmin の比はERest を与え、
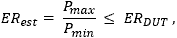
これはERDUT の推定値を与えることになります。ERref がERDUT よりも非常に大きい場合は、この推定値はより正確になります。詳細は下記セクション「高ERの参照用偏光子の使用」でご覧ください。なお、測定にノイズや実験誤差がないと仮定すると、ERest はERDUT より大きくなることはありません。
を正確に測定するのが困難な場合があり、その場合の測定誤差はERest の値に多大な悪影響を与える可能性があります。いくつかのガイドラインに従うことで、低パワー光の測定精度を向上させることができます。
この方法で推定するのは、光の消光比ではなくDUTの消光比の絶対値であることにご注意ください。
参照用直線偏光子の位置
光源の光が非偏光であるとみなされる場合は、DUTを光路内の参照用偏光子の前においても後においても、Pmax とPmin を測定できます。また、DUTと参照用偏光子のお互いの軸を平行または垂直にするために、どちらの偏光子を回転させても、あるいは両方を回転させても問題ありません。これは以下の式で見ることができます。
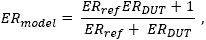
これは2つの部分偏光子のミュラー行列を乗じることで導くことができます。この導出では、両方の偏光成分が不完全であると仮定しているため、透過軸に対して垂直に偏光した光もある程度透過します。無限大の消光比を有する理想的な偏光子だけしか、透過軸に垂直な偏光を完全に透過しないようにはできないので、これは現実的な仮定です。光源が完全に非偏光の場合、この式で計算された値(ERmodel ) は、測定値(ERest )をモデル化したものになります。ERref とERDUTの値は1未満になることは無く、値が1の場合はNDフィルタを表します。[1]
多くの光源は、非偏光であると記載されていても、ある程度は偏光していることにご注意ください。その場合、偏光度(DOP)はゼロではなく、測定の要件と式はここで説明されているものとは異なります。光源のDOPを調べる1つの方法は、図1のセットアップからDUTを取り外し、直線偏光子を光軸を中心に回転させながら検出される光パワーをモニタすることです。直線偏光子を回転しても検出される光パワーが変化しなければ、光源は非偏光であるとみなすことができます。パワーメータのノイズフロアよりも大きな光パワーの変化が検出されたら、光源は部分的に偏光していることになります。
高ERの参照用偏光子の使用
参照用偏光子としては、DUTよりも非常に大きな消光比を有するものを選ぶことが重要です。ERmodel の式からわかるように(計算値は図2の青い曲線で示されています)、ERest の値は理論的に2つ偏光子の消光比のうちの小さい方の値を超えないように制限されます。また、ERmodel がERref よりも非常に大きい場合にのみ、ERDUT の値はDUTの消光比の実際の値に近づきます。参照用偏光子とDUTが同じタイプの偏光子である場合によくあることですが、これらの2つの偏光子の消光比がほぼ同じである場合、ERmodelはERDUT の約50%になります。
図9のグラフ内の赤い四角は実験データ(ERest )を示しています。この測定は消光比が既知の直線偏光子を使用して行われ、片方の偏光子を参照用直線偏光子、もう片方をDUTとして使用しました。
大きな消光比を有する適切な参照用偏光子が利用できない場合は、他の偏光子と組み合わせてセットとして使用することもできます。透過軸同士が互いに完全に平行になるように偏光子を揃えます。このセットの有効消光比(ERset )はそれぞれの偏光子の消光比の積であり、計算ではERref の代わりにERset を使用します。
参考文献
[1] Michael Kraemer and Tom Baur, "Extinction ratio measurements on high purity linear polarizers," Proc. SPIE Polarization: Measurement, Analysis, and Remote Sensing XIII, 10655, 1065505 (2018).
最終更新日:2021年5月16日
直線偏光の光源を使用して偏光子の消光比を測定する方法
試験対象の光学コンポーネント(DUT)の消光比は、レーザ光または直線偏光光源を使用して測定できますが、多くの場合、光源とDUTの間に直線偏光子を挿入する必要があります。よくあるケースですが、光源からの出力光の消光比がDUTの消光比よりも大幅に高くない場合には、直線偏光子が必要になります。DUTの消光比を正確に測定するには、入射光の消光比がDUTの消光比よりも非常に大きいことが必要です。1つまたは複数の直線偏光子を光源とDUTの間に挿入すると、DUTに入射する光の消光比を大きくすることができます。
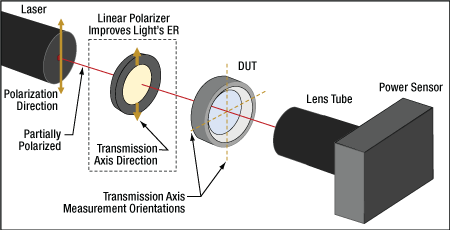
Click to Enlarge
図 10: 試験対象の光学素子(DUT)の消光比は、2つの光パワーの測定値から推定できます。1つ目のPmax を測定するときは、DUTの透過軸が入射光の偏光方向に対して平行(上図では鉛直方向)になっている必要があります。2つ目のPmin を測定するときは、DUTの透過軸が入射光の偏光方向に対して垂直(上図では水平方向)になっている必要があります。DUTへの入射光の消光比がDUTの消光比よりも非常に高い場合、より正確な推定値を得られます。光の消光比を向上させるために、光源とDUTの間に1つまたは複数の直線偏光子を挿入することが必要な場合があります。直線偏光と記載されているレーザからの光でも、消光比が低すぎて必要な精度が得られないことが多いためです。
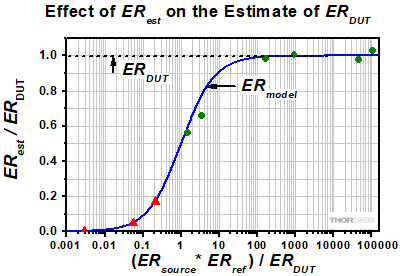
Click to Enlarge
図 11:DUTの消光比の測定値
DUTの消光比の推定
この方法で推定するのは、光の消光比ではなくDUTの消光比の絶対値であることにご注意ください。
DUTの消光比を正確に推定するには、DUTよりも消光比が非常に高い直線偏光の入射光と光パワーセンサが必要です。直線偏光の光源からの出射光が適切な消光比を有する場合もありますが(次のセクションを参照)、一般には光源とDUTの間に1つまたは複数の直線偏光子を挿入する必要があります(図1)。
DUTの消光比を推定するためには、2つの光パワーを測定する必要があります。光パワーセンサに到達する最大パワー(Pmax )を測定するには、DUTの透過軸を入射光の偏光方向に対して平行にする必要があります。DUTを透過する最小パワー(Pmin )を測定する場合は、DUTの透過軸を入射光の偏光方向に対して垂直にする必要があります。これら2つのDUTの透過軸方向は、図10では光源の偏光方向を鉛直方向であると仮定して金色の点線で示しています。
Pmax とPmin の比はERest を与え、
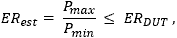
この値を用いてDUTの消光比
Pminを正確に測定するのが困難な場合があり、その場合の測定誤差はERest の値に多大な悪影響を与える可能性があります。いくつかのガイドラインに従うことで、低パワー光の測定精度を向上させることができます。なお、DUTの消光比を測定するのに非偏光の光源を使用することも可能です。
光源の消光比の向上
DUTに入射する光の消光比により、ERest の値がERDUT よりも非常に小さい値に制限される場合があります。ERest の値は、入射光の消光比がDUTに入射する光の消光比よりも非常に大きい場合にのみERDUT の値に近づきます。例えば、入射光の消光比がERDUT と等しい場合は、ERest の値はERDUT のわずか50%程度になります。入射光の消光比がERDUT よりも2桁大きい場合には、ERest はERDUT の約99%になります。
一般に、ほとんどのレーザからの出射光の消光比は非常に低いため、直線偏光子のような偏光特性の高いDUTの消光比を測定するのには適していません。そのような場合には、DUTの前に直線偏光子を挿入することにより(図10参照)、入射光の消光比を向上させることができます。同じ原理で、その位置に直線偏光子を追加すると、消光比がさらに向上します。高い消光比を得るには、この2つの偏光子の透過軸が正確に平行になるようにアライメントする必要があります。
入射光の消光比を向上させることの効果
ERest の値は、使用する光源の消光比や、光源とDUTの間に挿入する直線偏光子の有無などに応じてモデル化することができます。モデル化された値 (ERmodel )は、
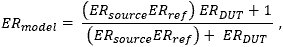
で与えられ、その値は図2に青い曲線で示しています。この式では、光源とDUTの間に直線偏光子を1つ挿入したと仮定しており、また光源の消光比はERsource で表しています。光源が非偏光の場合は、ERsource の値は1になります。この偏光子の消光比はERref です。複数の偏光子を挿入した場合は、ERref の値をそれらの偏光子の有効消光比に置き換える必要があります。光源とDUTの間に偏光子を挿入しない場合は、ERref の値を1に置き換えます。
直線偏光子とDUTの位置を入れ替え、DUTを光源に最も近い位置に置いた場合、その効果はこの式のERDUT とERref を入れ替えることでモデル化できます。そのように変更すると、モデル(および測定)によるERDUT の推定値は悪化します。最良の結果を得るには、直線偏光子のセットを光源に最も近い位置に置く必要があります。
参考文献
[1] Michael Kraemer and Tom Baur, "Extinction ratio measurements on high purity linear polarizers," Proc. SPIE Polarization: Measurement, Analysis, and Remote Sensing XIII, 10655, 1065505 (2018).
最終更新日:2021年5月16日
Insights:リフレクタ
スクロールするか下のリンクをクリックすると、推奨されるミラー径のほか、レトロリフレクタや金コーティング付きレトロリフレクタ内の光路などについてご覧いただけます。
- レーザのビーム径に基づいてミラー径を選択するルールはあるか
- ビームのアライメントはレトロリフレクタを通過するビーム光路にどのような影響を及ぼすか
- レトロリフレクタープリズムの裏面を金属コーティングする理由は
- コーナーキューブへの入射角は出射ビームのパワーに影響を及ぼすか
レーザのビーム径に基づいてミラー径を選択するルールはあるか
レーザのビーム径はミラーの有効径よりも大幅に小さくなければなりません(図1)。ビーム径はミラー径の1/3以下に制限するのが一般的なルールです。このようなルールに従うことで、ビームがミラー表面の周辺でコーティングの境界と相互作用したり、あるいは光学素子のエッジでクリップされたりすることで収差が生じるリスクを制限することができます。

Click to Enlarge
図1:ミラーの有効径は、ビーム径よりも大きい必要があります。一般的なルールでは、ビームの1/e2径より少なくとも3倍以上大きい径のミラーを使用することを推奨しています。

Click to Enlarge
図2:径の大きなミラーを使用すると、レーザースポットが完全にミラーの中心にない時や、斜めからの入射によりビーム径が引き延ばされた時にも、柔軟に対応してビーム品質を維持することができます。
ビーム径と光パワー
レーザ光がガウシアンの強度プロファイルを有する場合、ビーム径は1/e2の強度になるポイントで測定するのが一般的です。可視のビームを観察すると、通常1/e2径はビームを取り囲むように見えます。しかし、1/e2径における光の強度はピーク強度の13.5%であり、この直径の外側にも測定可能なパワーが存在します。
ミラーはビームの全パワーを反射するのに十分な大きさの直径(D )を有するのが最適です。反射されるパワーの比率(PT )は、
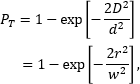
のように、Dと1/e2ビーム強度の径(d )、またはミラーの半径(r )と1/e2ビーム強度の半径(w )を使用して求められます。[1]
ミラーの径がビームの1/e2径より1.52倍大きい場合、ミラーはパワーの99%を反射できます。ミラー径を大きくしてビーム径の2倍にした場合、パワーの99.96%を反射します。ビームが完全にミラーの中心にない場合、反射される光の割合は小さくなります。
ビーム位置と有効径
ミラーの光学性能は有効径の全領域に対して定められますが、この有効径にはミラー周辺の細い円環部分は含まれません。レーザ光を有効径内に制限するのは、ミラー周辺部の性能が知られてないため適切な方法です。また、有効径からはみ出た光は、ミラーのエッジでクリップされるリスクがあります。
ミラー径がビーム径の2倍あり、かつビームが完全にミラーの中心にある場合、ビームの光学的品質は維持され、ビームのほぼすべてのパワーが反射されます。しかし、何らかのミスアライメントがあれば、ビームの品質は影響を受けます。より大きなミラーを使用すると、アライメント時に柔軟性が得られ、ビームが完全に有効径の中心にない場合にも対応できます。そのため、ビーム径より少なくとも3倍以上大きい有効径を有するミラーを使用することが有用です。
ビームアライメントに関する追加情報は
こちらの動画ページでご覧ください。
参考文献
[1] Bahaa E. A. Saleh and Malvin Carl Teich, Fundamentals of Photonics (John Wiley & Sons, Inc., New York, 1991) p. 85.
最終更新日:2020年10月12日
ビームのアライメントはレトロリフレクタを通過するビーム光路にどのような影響を及ぼすか
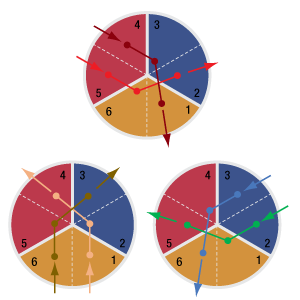
Click to Enlarge
図4:ビームが反射されるシークエンスは6通りあります。そのシークエンスは最初にビームが反射される領域によって決まります。上の図は、レトロリフレクタのノーマル軸(本文参照)とほぼ平行な入射ビームに適用されます。矢印はビームの光路、点は反射される位置を示しています。
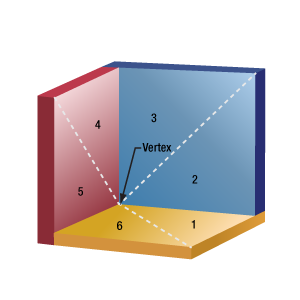
Click to Enlarge
図 3:図ではコーナーキューブの3つの反射面をそれぞれ色分けして示し、さらにその半分の面を数字で示しています。レトロリフレクタは、入射ビームをそれぞれの面で反射し、入射ビームに平行なビームを出射するように設計されています。
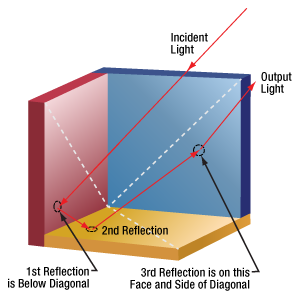
Click to Enlarge
図6:最初に反射される位置を赤色の面の斜線より下の位置にシフトすると、次は黄色の面で反射されます。青色の面での3回目の反射の後、ビームは図5の出射ビームと平行に出射しますが、その出射面は変化しています。
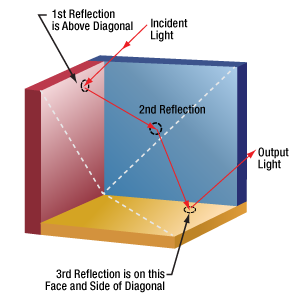
Click to Enlarge
図5:ビームがレトロリフレクタのノーマル軸に平行に入射し、最初に赤色の面の斜線より上の位置で反射されたときは、次に青色の面で反射されます。その後、ビームは黄色の面で反射され、レトロリフレクタから出射します。
コーナーキューブから出射したビームは、入射ビームに対して平行に、しかし入射ビームとは反対方向に伝搬します。入射ビームはコーナーキューブの頂点、あるいは3面のうちの1つの面上の1点にアライメントすることができます。 入射ビームが頂点にアライメントされているときは、入射ビームと出射ビームは同一線上にあります。入射ビームのスポットが頂点と重ならないときは、2つのビームは分離します。
レトロリフレクタの面の1つにアライメントされた入射ビームは、その面で反射されたのち、レトロリフレクタから出射されるまでに他の2つの面で反射されます。入射角により、ビームが3つの異なる面で反射されるシークエンスは6通りあります。レトロリフレクタ内を通過する光路を選択することは、ビーム位置を最適化し、また偏光に対する影響を最小化するという観点から、非常に有用です。
ビームを特定のシークエンスで反射させたいときには、1つの面に入射するようにビームをアライメントするだけでは不十分です。ビームをその面の適切な半分の面内に入射しなければなりません。
ビーム光路の追跡
レトロリフレクタの頂点を正面から見ると、反射の効果により、3つの面のそれぞれ半分の面に対応する6つの面を見ることができます。ここで、それらの面は斜めの点線で分離して識別されています(図3)。さらに、見やすくするために、レトロリフレクタの3つの面をそれぞれ色分けして示しています。ノーマル軸は図に示されていませんが、頂点を通り、3つのすべての面から等距離にあります。
6通りある反射のシークエンスは、入射角によって異なります。図4はノーマル軸にほぼ平行に入射するビームに対して適用されます。これらの図では中空レトロリフレクタが使用されていますが、反射のシークエンスはプリズムミラーにも当てはまります。
最初に反射された位置により、ビームがレトロリフレクタ内で反射されるシークエンスが決まります。ビームは常に入射面とは異なる面から出射します。
例
図5と6は、入射ビームが最初に左端の垂直な面で反射された時に生じる、2通りの反射の様子を示しています。入射ビームはレトロリフレクタのノーマル軸に平行です。
図5のように、入射ビームが最初に斜線より上の位置で反射されたときは、最後の反射面は水平な面(黄色)になります。一方、入射ビームが最初に斜線より下の位置で反射されたときは、最後の反射面はもう一つの垂直な面(青色)になります。この2つのケースで、出射するビームは互いに平行ですが、その位置は異なっています。
最終更新日:2020年7月8日
レトロリフレクタープリズムの裏面を金属コーティングする理由は
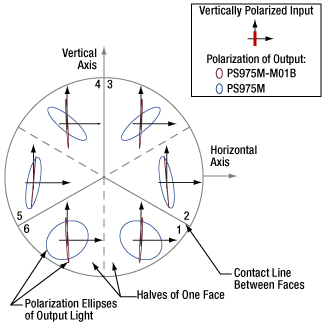
Click for Details
図8:垂直偏光ビームを内部全反射型のレトロリフレクタープリズム(PS975M)と、裏面に金コーティングが施されたレトロリフレクタープリズム(PS975M-M01B)に入射した結果を示しています。各出射ビームの偏光楕円は、ビームが3回目に反射する領域に示されています。水平軸に対する楕円率角( χ )と方位角( ψ )のグラフはこちらをご覧ください。
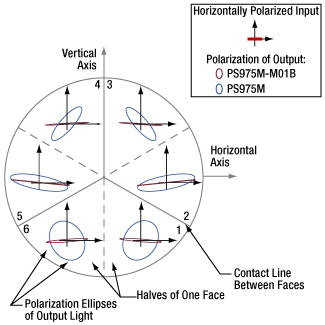
Click to Enlarge
図 7:水平偏光のビームを内部全反射型のレトロリフレクタープリズム(PS975M)と、裏面に金コーティングが施されたレトロリフレクタープリズム(PS975M-M01B)に入射した結果を示しています。各出射ビームの偏光楕円は、ビームが3回目に反射する領域に示されています。水平軸に対する楕円率角( χ )と方位角( ψ )のグラフはこちらをクリックしてご覧ください。
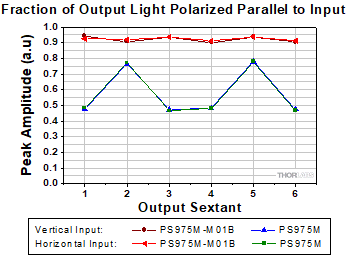
Click to Enlarge
図10:レトロリフレクタは入射光の一部を、入射光の偏光とは直交する偏光に変換します。裏面が金コーティングされたレトロリフレクタープリズム(PS975M-M01B)から出射する光の90%以上は、入射時の偏光状態を維持していました。内部全反射型のレトロリフレクタープリズム(PS975M)の場合、その割合は光路に大きく依存し、80%を超えることはありませんでした。

Click to Enlarge
図 9:レトロリフレクタは、入射ビームが各面で1回反射されるように設計されています。ビームが図7および8の面(紙面)に対してほぼ垂直に入射したとき、ビームは6通りの光路のうちの1つをたどります。
レトロリフレクタープリズムの裏面に金属コーティングが施されていると、出射ビームにおける偏光の変化が大幅に抑えられます。
これは、鏡面反射と内部全反射の違いによるものです。鏡面反射はガラスとガラスよりも屈折率の大きな金属の界面で生じ、内部全反射(TIR)が生じるには裏面側に空気のような屈折率の小さな物質が必要です。
ガラスと金属の界面において発生する鏡面反射では、内部全反射に比べて入射ビームの偏光楕円率が良く保存されます。
偏光と光路
レトロリフレクタを通る光路は、3つの反射面をさらに6つのクサビ形に分割することで表現することができます(図7、8、9)。実線は反射面が物理的に接触する線を示します。点線は各反射面を半分に分ける境界を示しています。
これらの図のレトロリフレクタの各反射面は、紙面に垂直な軸に対してそれぞれが同等に対面するように向かい合っています。図9は、入射ビームが図の面(紙面)に対して垂直な場合について、ビームが入射してから出射するまでの反射の順序を示しています。
出射光の偏光状態
内部全反射型のレトロリフレクタープリズム(PS975M)と裏面が金コーティング付きのレトロリフレクタープリズム(
図7と8の出射ビームの偏光状態は、偏光楕円を用いて表されています。それぞれの出射ビームの偏光楕円は、3回目に反射される領域内に示されています。
出射ビームは入射ビームと同じ偏光状態を持つことが理想的です。しかしこれらの測定結果は、レトロリフレクタが入射光の一部を、入射光の偏光とは直交する偏光に変換していることを示しています。図10のグラフは、出射ビーム中における、入射光の偏光方向と平行な偏光成分の割合の測定値です。
裏面に金コーティングが施されたレトロリフレクタープリズムでは、入射した直線偏光の偏光状態が大変よく維持されます。
最終更新日:2020年7月7日
コーナーキューブへの入射角は出射ビームのパワーに影響を及ぼすか
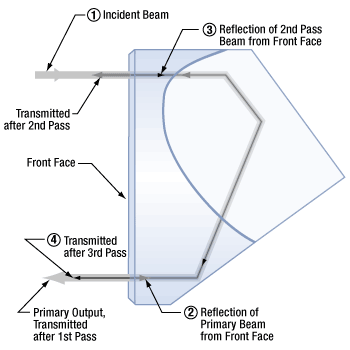
Click to Enlarge
図 12:ガラスと空気の屈折率は異なるため、ビームは前面で反射します。反射された光は出射するまでにレトロリフレクタ内を複数回通過する場合があります。重ねられたコヒーレント光により干渉が生じます。
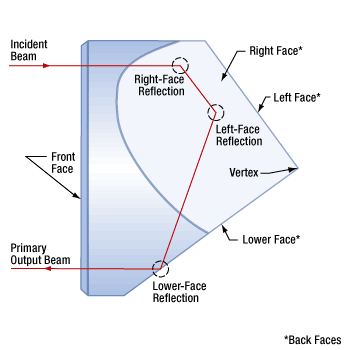
Click to Enlarge
図11:コーナーキューブレトロリフレクタを通過するビームは後方の3つの面で反射され、その順序はビームの入射位置によって決定されます。上図に示す入射ビームの入射角は0°で、頂点から外れています。
レトロリフレクタープリズムからの出射光のパワーは、入射角(AOI)が変化すると平均値のまわりで振動する場合があります。これは、多重反射干渉によるもので、光源のコヒーレント長がレトロリフレクタ内の光路長の2倍以上あるときに生じることがあります。
レトロリフレクタの前面に反射防止コーティングが施されていると、この変動はすべての入射角において大幅に小さくなります。金属コーティングされた中空レトロリフレクタの出射ビームパワーは、入射角にほぼ依存しません。
光路
これらのコーナーキューブレトロリフレクタでは、入射ビームに対して平行で、かつ反対方向に伝搬するビームが出射されます。図11では1つのビーム路を示しています。
入射角は、レトロリフレクタの前面に垂直な軸を基準にしています。この軸は頂点を通り、また3つの反射面から等距離にあります。
前面での反射
図12に示すように、光はレトロリフレクタの表面と周囲の物質の境界面において反射するかあるいは透過するかによって、レトロリフレクタ内を複数回通過する場合があります。
ガラス製のレトロリフレクタが空気に囲まれているとき、入射光の約96%はレトロリフレクタ内を1回通過(図12の1st Pass)して最初に出射する主たるビームとなり、約0.16%はレトロリフレクタ内をもう1巡(図12の3rd Pass)してから出射します。さらに巡回する光の強度は、ここでは無視できます。
干渉の条件
レトロリフレクタープリズムの出射光は異なる光路長を伝播するビームから構成されているため、次の条件のときに干渉が生じます。
- ビームが重なっている。これは入射ビームの入射角が0°に近く、出射光の測定位置がレトロリフレクタに近い場合により生じやすい条件です。より離れた位置で測定した場合、レトロリフレクタの仕様に基づくビームのずれと入射角の影響により、1st Passと3rd Passの出射光はより大きく分離します。
- 光源のコヒーレント長が、1st Passの光路長とそれに重なる3rd Passの光路長との差よりも長い。
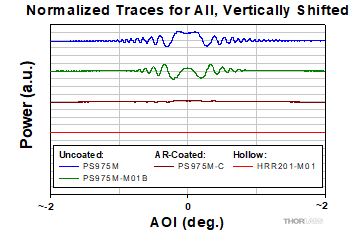
Click to Enlarge
図14:出射光パワーの入射角依存性の、コーナーキューブレトロリフレクタの種類による差異。図13と同じ方法で測定したデータを、同様に同じスケールで規格化し、見やすいように各グラフを垂直方向にシフトして示しています。前面にARコーティングが施されているリフレクタ
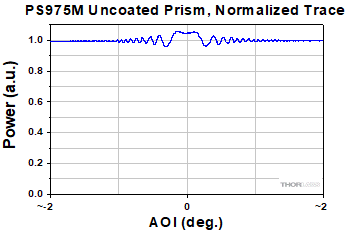
Click to Enlarge
図13:内部全反射レトロリフレクタープリズム(PS975M)の出射光パワーの入射角依存性(測定値)。入射ビームの光源は1064 nmレーザ光源DBR1064Sで、そのコヒーレンス長は数メートルです。 最大の振幅は入射角0°付近にみられ、ここでは1st Passと3rd Passの出射光は重なっていました。1/e2ビーム径は、レトロリフレクタの前面から30 cmの位置で、±1°より大きい入射角では重なりませんでした。
コーナーキューブレトロリフレクタの比較
小さい入射角での出射光パワーの変化を、次の4種類のコーナーキューブレトロリフレクタで比較しました(内部全反射レトロリフレクタープリズムPS975M、裏面に金コーティング付きのレトロリフレクタープリズム
図13は内部全反射レトロリフレクタープリズムの測定値で、グラフは規格化されています。入射角が大きくなると、1st Passと3rd Passの出射ビームは互いに離れていきました。入射角が約±1°より大きくなると、ビームの1/e2径は重ならなくなりました。これにより振幅は入射角の増加とともに小さくなりました。ディテクタの位置をレトロリフレクタの前面に近付けると、振動が著しい入射角の範囲は大きくなります。
図14では、図13のグラフにほかの3種類のレトロリフレクタの測定データを加えています。同じスケールに規格化していますが、見やすいよう垂直方向にシフトさせています。この結果から、前面にARコーティングを施すと、レトロリフレクタープリズムからの出射光におけるパワー変動の振幅を抑えられることが分かります。中空レトロリフレクタの出射光パワーが変動しないのは、前面に物質の境界面が無いためです。
最終更新日:2020年7月7日
デジタルマイクロメータDM713: LabVIEWおよびC#プログラミングリファレンス

Click to Enlarge
図 1:デジタルマイクロメータDM713の測定値を読み取るためのプログラムを、Visual C#やLabVIEWで書くことができます。プログラミングリファレンスをダウンロードすると、その詳細な例をご覧頂けます。
デジタルマイクロメータDM713(図1)と通信する方法を紹介したプログラミングリファレンスをご提供しています。1つはLabVIEW用、もう1つはVisual C#用です。どちらのリファレンスにも、プログラムを作成するまでを順を追って説明したセクションと、説明無しで全プログラムテキストを簡潔に記載したセクションが含まれています。
- ドライバーソフトウェアのダウンロードとインストールの方法
- DM713のCOMポートへの接続ケーブルと接続方法についての情報
- DM713とのシリアル通信を行うための新VIの作成
- DM713からのデータの連続受信
- 変位データとその測定単位の表示
- ボタンのクリックによるデータの記録
- DM713のCOMポートにPCを接続するための情報
- DM713と連続的に通信するためにセカンダリスレッドを生成する方法
- 変位データと単位を抽出するための受信データの操作手順
- プログラムのGUIに変位データと単位を表示する方法
- ボタンのクリックによる変位データのファイルへの記録
最終更新日:2019年12月4日
1
フォトニクス実験のためのHow-To動画集
何かを学ぶ上で、誰かが行っているのを見ることが最良の方法である場合があります。ここではそのような動画を提供し、私たちが実験室でよく使用しているコツや秘訣、方法などを共有していきたいと考えています。ご質問等は当社までご連絡ください。
※動画は英語の音声、日本語の字幕付きでご覧いただけます(一部除く)。
レーザのアライメントとセットアップ:
- レーザのアライメント方法
- 2本のシングルモードファイバから出力された光を自由空間を介して結合するためのファイバーコリメータのアライメント方法
- TO-Can型半導体レーザのセットアップ(Viewer Inspired)
- ピグテール付、バタフライパッケージ型半導体レーザのセットアップ(Viewer Inspired)
偏光:
- 直線偏光子の軸をテーブルに対して垂直または平行にアライメントする方法
- 直線偏光子を入射面に対して45°にアライメントする方法
- 1/4波長板(QWP)を使用して円偏光に変換する方法
- 1/4波長板のファスト軸とスロー軸を区別する方法
- 偏光計を構築して、ストークス値と偏光状態を特定する方法(Viewer Inspired)
- New! 光の透過率とブリュースター角の入射角依存性
光学素子と光デバイス:
- 追尾機能を備えた太陽撮像望遠鏡の構築
- シヤリングプレートコリメーションテスタを用いてレーザをコリメートする方法(Viewer Inspired)
- レーザースペックルを利用してビームの焦点を見つける方法
- 精度を高めるための光パワーメーターパラメータの設定方法
- 軸外放物面(OAP)ミラーをアライメントしてビームをコリメートする(Viewer Inspired)
- 空間光変調器(SLM)の位相遅延の校正方法
- ヘリオットセルのセットアップと構成(Viewer Inspired)
- LEDからの出力光をコリメートする方法
- アイソレータの調整方法
光ファイバ:
- ハンドヘルド型スクライブを使用して大きな直径の石英ファイバをクリーブする方法
- 偏波保持ファイバに結合する光の偏光方向をアライメントする方法(Viewer Inspired)
- 光ファイバ用コンポーネントの挿入損失測定
- FiberBench上でのFiberPortのアライメント(Viewer Inspired)
オプトメカニクス:
- ポストホルダを光学テーブル、ベース、ブレッドボードなどにボルトで固定するときの注意点
- ベース、ポストホルダ、ポストなどを取り付ける際の注意点
- 手動ステージを電動ステージに交換する方法
- KF(QR)真空フランジの使い方
- 真空対応CF(コンフラット)フランジの使い方
ソフトウェアのチュートリアル:
- Visual Studio®プロジェクト作成とC#プログラミング: Kinesis® BBD300シリーズ
- Visual Studio®とC#プログラミングによるラスタスキャン:Kinesis® BBD300シリーズコントローラを使用して
- Visual Studio®とC#プログラミングでカメラをセットアップし、画像を取得する
- Python® による回転マウントとパワーメータの自動制御 (Viewer Inspired)
最終更新日:2024年5月7日
レーザのアライメント方法
レーザービームが光学テーブルの表面に水平に伝搬するようにアライメントする方法を2つご紹介します。
最初の方法では、レーザービームのあおり調整(チップ&チルト)を行い、ポインティング角度の調整を行います。ルーラを使用して、レーザービームの高さを調整するとともに、テーブルのタップ穴の列に沿うように向きを調整します。
2つ目の方法として、この調整済みのビームを用いて、固定されたレーザ光源からのビームの向きと高さの両方を変更する方法を実演します。異なる高さに設定された2つのミラーを用いて、ビームをテーブルの別のタップ穴の列に沿うように向けます。次に、2つのアイリスを用いて、ビームの高さを2つ目のミラーの高さに合わせます。
| Products Featured During Demonstration | ||
| Laser Module | Kinematic Mounts | Irises |
| Adapter (Laser to Mount) | Mirrors | Ruler |
最終更新日:2020年9月8日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 1 |
パワーメータの精度を高めるための、波長、レンジ、およびゼロオフセットパラメータの設定方法
パワーメータはパワーセンサへの入射光に合わせて設定を構成する必要があります。パワーメータを設定する際の重要な3つのパラメータは、光の中心波長、測定しようとする光パワーの最大値、および周囲の光を検出することによるゼロオフセットです。
この3つのパラメータの設定方法とそれらを設定時に考慮すべき事項についてを実演し、解説をしています。
必ず所属する研究機関等のレーザ安全ガイドラインに従ってください。この実演で使用されている低パワーの光源とは異なる他のレーザ光源を使用した場合は、後方反射によってレーザが損傷する可能性があります。人体やレーザに対して危険な迷光反射の影響は、不要なときにはレーザービームをブロックすることで軽減することができます。
| Products Featured During Demonstration | ||
| Optical Power Meter | Optical Power Sensor | Fiber-Coupled Laser Source |
最終更新日:2020年9月24日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 2 |
移動ステージの設置方法と電動アクチュエータの取付け方
ここでは、移動ステージに取付けられている手動アジャスタを電動アクチュエータに交換する方法を、2つの例で実演しています。ここでご紹介している方法を用いることで、ステージを傷つけることなくアジャスタを交換できます。
最初の例では、移動量12.7 mmのリニア移動ステージMT1B(/M)を使用します。調整ネジをステッピングモーターアクチュエータZFS13Bに交換します。動画後半の2番目の例では、移動量25.4 mmのリニア移動ステージXR25P(/M)のマイクロメータを、DCサーボモーターアクチュエータに交換します。
また、これらのステージをテーブルやブレッドボードに取り付ける際の最適な方法や、ロッキングプレートの使用方法についてもご紹介しています。
| Products Featured During First Half of Demonstration | Products Featured During Second Half of Demonstration | |||
| Linear Translation Stage | Stepper-Motor-Driven Actuator | Linear Translation Stage | DC-Servo-Motor-Driven Actuator | |
最終更新日:2023年11月11日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 3 |
ポストホルダを光学テーブル、ベース、ブレッドボードなどにボルトで固定するときの注意点
ポストホルダをベースやテーブルに固定する際に、ネジがポストホルダの底部から突き出ていて困ることがあります。そのようなネジが突き出た状態では、ポストホルダの高さ調整範囲が制限されてしまいます。さらに、ポストをポストホルダ内で回転したときに、意図せずに突き出たネジにポストをねじ込んでしまう場合もあります。
これを防ぐ方法は、ポストホルダを固定するためのセットスクリュまたはキャップスクリュを選ぶ際に、それらのネジの長さを考慮に入れることです。この動画では、ポストホルダの底部から突き出たネジによって生じる問題と、その解決方法をご紹介します。また、ポストホルダをベースに固定する場合とテーブルに直接固定する場合についての比較も行っています。
こちらの動画の続編では、オプトメカニクスを使用して光学系に安定した基礎を構築し、またコンポーネントの偶発的な損傷を防ぐのに役立つヒントなどをご覧いただきます。
| Products Featured During Demonstration | ||
| Ø1/2" Post Holders | Mounting Base | Cap Screws |
| Ø1/2" Posts | Iris | Setscrews |
最終更新日:2022年4月28日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 4 |
フリースペース型アイソレータのレーザ波長に応じた調整
ファラデーアイソレータを調整することで、光源からの光パワーを適切に透過させ、光源に向かって戻る反射光を効果的に抑えることができます。この実演では、動作波長範囲が510 nm~550 nmの偏光依存性を有するフリースペース型アイソレータと、520 nmのコリメート光を出力する直線偏光レーザを使用しています。
これらの光学アイソレータからは直線偏光が出射され、また入射光が直線偏光のときに最良の性能が得られます。
必ず所属する研究機関等のレーザ安全ガイドラインに従ってください。この実演で使用されている低パワーの光源とは異なる他のレーザ光源を使用した場合は、後方反射によってレーザが損傷する可能性があります。人体やレーザに対して危険な迷光反射の影響は、不要なときにはレーザービームをブロックすることで軽減することができます。
| Products Featured During Demonstration | ||
| Free-Space Isolator | Power Sensor | Post Collar |
| Laser | Power Meter | Balldrivers and Hex Keys |
最終更新日:2020年9月10日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 5 |
直線偏光子の軸をテーブルに対して垂直または平行にアライメントする方法
多くの光学セットアップの光路は、光学テーブルに対して平行になるようにセットします。この場合、一般には入射面とp偏光の向きはテーブル面に対して平行に、s偏光の向きはテーブル面に対して垂直になります。したがって、pまたはs偏光が通過するようにアライメントされた偏光子の軸は、テーブル面に対してそれぞれ平行または垂直になるようにアライメントされます。
偏光子を透過する光パワーの読み取り値を用いて、偏光子の軸を光学テーブルに対して垂直になるようにアライメントする手順について、説明と実演を行います。次に、偏光子の軸をテーブル面に水平にアライメントする3つの方法の概要について説明し、直交する偏光子を使用した方法を実演しています。より正確な測定値を得るためのヒントやコツについてもご紹介しています。
| Products Featured During Demonstration | |||
| Collimated Laser | Polarizing Beam Splitter | Optical Power Sensor | Post Collar |
| Linear Polarizers | Precision Rotation Mounts | Power Meter | Ruler |
最終更新日:2020年10月23日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 6 |
ハンドヘルド型スクライブを使用して大きな直径の石英ファイバをクリーブする方法
ハンドヘルド型スクライブを用いて大きな直径の光学ファイバを手でクリーブすることで、光学的品質の優れたファイバ端を得ることができます。コア径400 µmのマルチモードファイバを使用してその手順を実演します。
ファイバ端から保護ポリマのバッファを除去し、ファイバをフラットな面に固定します。次に、ハンドヘルド型スクライブでファイバの外側の面に切り込みを入れます。スクライブでは、ファイバのコア部分から離れたファイバのクラッド部分に、浅く切り込みが入るようにしてください。直径の小さなファイバをクリーブする場合は、力を加減しながらゆっくりとスクライブを行い、切り込みを深く入れすぎないようにしてください。スクライブを動かさず、軽くファイバに押し付けるだけで十分な場合もあります。切り込みを入れた部分を挟んで縦方向に力を加えてクリーブします。
アイルーペを使ってファイバ端の状態を目視で評価する方法も実演しています。品質の良い端面はファイバの縦軸に対して垂直でフラットな面になっています。クリーブされた端面からの出射光をスクリーンで観察し、その強度分布から端面の品質に関する情報を得る方法なども紹介しています。
最終更新日:2020年11月3日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 7 |
光ファイバ用コンポーネントの挿入損失測定
挿入損失は、光ファイバーネットワークにデバイスを追加することで発生する光パワーの低下を測定することで得られます。デバイスの挿入損失の原因となる光学的損失には、素材固有の特性による反射、吸収、散乱のほか、マイクロベンディング損失および曲げ損失、分岐比、接続損失、コネクタ損失などが含まれます。
動画では、シングルエンド挿入損失の測定方法を実演しています。このアプローチでは、まず参照用ケーブルを光源に取り付け、そのケーブルから出力される光パワーを測定します。次に、アダプタを使用して試験対象のコンポーネントを参照用ケーブルに取り付けます。取付けられたコンポーネントの選択した出力ポートからの光パワーを測定します。挿入損失は、このパワーの読み取り値と参照用ケーブルからの出力光パワーの測定値との比を求め、その比をデシベル(dB)単位で表します。
シングルエンド挿入損失の測定値には光がデバイスに結合する際の損失が含まれますが、その主たる原因がアダプタ内のファイバーコアのミスアライメントによる場合が多く見られます。しかし、この測定値には、デバイスからの出力光がファイバーネットワークの次のコンポーネントに結合するときに発生する損失と同じタイプの損失は含まれていません。また、挿入損失は波長に依存し、測定時のデバイスの入力ポートおよび出力ポートの組み合わせによって異なるということにもご注意ください。これは、分岐比、曲げ損失、吸収、散乱、反射、および2つのポート間の光路に沿った他のすべての減衰要因の違いによるものです。
| Products Featured During Demonstration | |||||
| Fiber-Coupled Laser Source | Mating Sleeve | Power Sensor | Power Meter | 50:50 Coupler | Single Mode Patch Cables |
最終更新日:2020年12月3日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 8 |
1/4波長板を使用して円偏光に変換する方法
直線偏光ビーム対して1/4波長板を置くことで円偏光に変換できますが、いくつかの条件を満たす必要があります。1つは光の波長が波長板の動作範囲内にあることです。もう1つは、波長板の直交するスロー軸とファスト軸が、直線偏光の偏光方向に対して45° の位置にセットされていることです。この条件が満たされたとき、入射光の2つの軸に平行な成分の強度は等しくなります。波長板は、スロー軸に平行な成分を、ファスト軸に平行な成分に対して1/4波長分(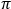 /2)だけ遅延させます。この遅延効果により、直線偏光は波長板で円偏光に変換されます。
/2)だけ遅延させます。この遅延効果により、直線偏光は波長板で円偏光に変換されます。
動画の最初では、直線偏光の偏光方向を波長板のファスト軸、スロー軸、およびその間の角度に設定して入射したときに得られる結果を図解しています。角度や向きは、光の伝搬方向の逆方向から光源を視る見方で描かれています。次に、入射光側の偏光子と出射光側の偏光子を互いに直交する方向に設定し、偏光によって変化するパワーを測定する手順を紹介します。波長板を2つの偏光子の間に挿入し、向きを変えてその影響を調べます。波長板から出射された円偏光の品質は、2番目の偏光子の透過軸を回転させることで確認できます。回転したときのパワーの読み取り値の変化が小さければ、光はより円偏光に近いことになります。
| Products Featured During Demonstration | ||||
| HeNe Laser | Quarter-Wave Plate | Precision Rotation Mounts | Power Sensor | Power Meter |
| Optical Isolator (for HeNe) | Linear Film Polarizers | V-Clamp Mount | SM1 Thread Adapter (for Power Sensor) | SM1 Lens Tube |
最終更新日:2020年12月30日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 9 |
直線偏光子を入射面に対して45°にアライメントする方法
直線偏光子の透過軸は、2枚の直線偏光子を補助的に使用することで、入射面に対して45°に設定することができます。まず、補助的な2枚の直線偏光子の軸を、入射面に対してそれぞれ平行および垂直になるようにアライメントします。次に3枚目の偏光子の透過軸を回転させて前述の2枚の偏光子の軸に対して45°の角度にすると、その透過軸は入射面に対して45°になります。
動画では、入射面が光学テーブルに対して平行な場合について実演しています。1枚目の偏光子の軸をテーブルに対して平行にアライメントする手順では、偏光子を垂直軸の周りに180°回転させる操作を繰り返し行う必要があります。直線偏光子アセンブリは長方形のベースを用いており、固定式位置決めプレート(フォーク)を用いてコーナの位置決めができます。このフォークにより、偏光子アセンブリを垂直軸回りに反転させた後も、素早く正確に元の位置に設置できます。180°の反転操作のたびに、偏光子の透過軸を最初は手動で回転させ、最後にはマウントに取付けられているマイクロメータ(mic)で微調整します。1枚目の偏光子の軸がアライメントできたら、2枚目の偏光子の軸をそれに直交させます。このとき、2枚目の偏光子の透過光は最小になります。
3枚目の偏光子を他の2枚の偏光子の間に設置し、透過軸を回転させます。その回転角度により3枚の偏光子を透過する光のパワーは変化し、入射面に対して45°のときに透過光パワーは最大になります。この結果を確認し、またディテクタで検出される可能性のある最大光パワーを見積もる1つの方法として、余弦二乗法則(マリュスの法則)を利用する方法があります。これを利用することで、直線偏光子への入射光が直線偏光の場合の出射光パワーを算出することができます。
| Products Featured During Demonstration | ||||||
| Laser Module | Linear Film Polarizers | Precision Rotation Mounts | Power Sensor | SM1 Thread Adapter (for Power Sensor) | Power Meter | SM1 Lens Tube |
最終更新日:2021年2月8日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 10 |
2本のシングルモードファイバから出力された光を自由空間を介して結合するための
ファイバーコリメータのアライメント方法
光ファイバのセットアップの間に2つのコリメートレンズを挿入することによって、様々なビームへの操作が可能な自由空間光を得ることができます。1つ目のコリメータは出射側ファイバからの発散光を受光し、それによってコリメートされた自由空間ビームは2つ目のコリメータに向けてほぼ一定の径で伝搬します。2つ目のコリメータは自由空間ビームを受光し、受光側のファイバに結合します。こちらの動画においてペアで使用されているコリメーターパッケージのように、ファイバを直接ファイバーコネクタに接続するように設計されている製品がございます。
出射側のファイバからの光を100%の効率で受光側のファイバに結合できれば理想ですが、実際には常に反射、散乱、吸収、ミスアライメントなどによって損失が生じます。通常、光損失の最も大きな原因となるミスアライメントは、こちらの動画でご紹介しているアライメント法や安定化の方法により最小化することができます。
この動画では、出射側のファイバとしてシングルモードファイバを使用しています。2つ目のコリメータに入射する光パワーと、受光側のファイバから出射される光のパワーを測定しています。受光側のファイバがコア径50 µmのマルチモードファイバの場合、アライメントを行うことで、2つ目のコリメータに入射した光パワーの91%が受光側ファイバからの出射光として測定されました。受光側のファイバがシングルモードファイバの場合、この値は86%になりました。動画では、コリメータの設計の違いと、その違いがコリメート光の特性に及ぼす影響などについてもご説明しています。
| Products Featured During Demonstration | ||||
| Fiber-Coupled Laser | Kinematic Mounts | Fiber Adapter Cap (for Power Sensor) | Single Mode Patch Cable (FC/PC) | Fiber Cable Storage Reels |
| Triplet Fiber Optic Collimators | Power Sensor | Power Meter | Hybrid Single Mode Patch Cable | 2" Posts |
| Adapter (Mount-to-Collimator) | SM1 Thread Adapter (for Power Sensor) | Fiber Connector Cleaner | Step-Index Multimode Patch Cable | 0.5" Post Holders |
最終更新日:2021年4月1日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 11 |
TO-Can型半導体レーザのセットアップ(Viewer Inspired)
TO-Can型半導体レーザをマウント内に取り付けて、温度と電流の制御下で動作するように設定する際、誤ってレーザに損傷を与えたり破損したりする可能性が多くあります。このガイドでは、人体と半導体レーザを損傷の危険から守る方法を順を追ってご説明しています。
静電気放電(ESD)によるレーザ破損の危険を避けるために、ESDストラップをご提供していますが、これはストラップが接地し、正しく装着されている場合にのみ有効です。動画のようにストラップを装着すると、ストラップの金属プレート部分が常に肌に接触される状態になります。静電気の生じやすい環境やクリーンルーム環境で使用する場合は、ローションで肌に潤いを与えるとより良いでしょう。
TO-Can型半導体レーザは、間違ったサイズのソケットに無理やり押し込もうとすると破損する可能性があります。そのため、動画で紹介しているピンの寸法を参考にし、適切なマウントを見つけてください。 半導体レーザに誤った方向で電流を流すことも危険なため、ソケット内のレーザを正しい向きにし、マウントのスイッチの極性を正しく設定することも重要です。通常、電流ドライバにも極性の設定があります。ダイオードの方向と、マウントおよびドライバの設定については、レーザのピン配列もしくは回路図に記載の情報を確認して決定してください。記号の意味はビデオ内で説明されています。
過剰な動作温度と駆動電流はどちらも危険ですが、正しく設定された電流および温度コントローラを使用することでリスクは低減されます。そのセットアップについては動画で実演されています。電流ドライバを設定する際に誤解が生じやすい2つのパラメータや、最大パワーおよび最大電流を適切に使用する方法も示されています
最終更新日:2021年5月7日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 12 |
ピグテール付、バタフライパッケージ型半導体レーザのセットアップ(Viewer Inspired)
バタフライパッケージ型の半導体レーザは、TECコントローラと電流コントローラ付きのマウントに取り付けることにより、コンパクトなパッケージで精密な制御が可能となります。このマウントにより、レーザの取り扱いはより簡単で安全になりますが、レーザをマウントに取り付ける際には様々な注意が必要です。こちらの動画では半導体レーザの取り付けや設定に関するガイドとなっています。始めに様々な関連部品について説明し、温度制御、最大電流リミット設定など、レーザ操作に必要な手順をご紹介します。
こちらのでデモでは「セットアップの手順では触れられていない有益な情報」についても説明しています。例えば、静電気防止用ESDストラップの着用、熱グリースをいつ使用するかの判断方法、熱グリースの適量、レーザのピンとマウントの電気接続方法、マウントから簡単にレーザを取外す方法、取り付けたレーザのファイバーピグテールの保護方法、APCコネクタのクリーニング方法、レーザの仕様書に書かれたSteinhart-Hart式サーミスタの値の使用、レーザの電流リミットの設定値を決定するためのパワー測定などについて説明しています。
最終更新日:2021年6月17日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 13 |
波長板のファスト軸とスロー軸を区別する方法
波長板には2つの軸があります。スロー軸に平行な偏光成分は、それに直交するファスト軸に平行な偏光成分に対して遅延します。波長板のリターダンスがこの遅延量を決定します。複数の交差する偏光子を使用することで軸を特定することはできますが(動画参照)、それがファスト軸とスロー軸のどちらであるかについては識別できません。しかし、セットアップにミラーを追加し、光パワーの計算値と測定値を比較することで、ファスト軸とスロー軸を区別することができます。この方法はあらゆるリターダンスの波長板に適用できますが、右の動画では1/4波長板を使用しています。
この動画では、測定用セットアップの概要と、光学部品のアライメントや向きに関する慣習などについて解説しています。結果の正確な解釈は、偏光子と検光子の透過軸が平行か直交(交差)かなど、セットアップの詳細に依存します。ここの動画では交差偏光子が使用されており、この方法について解説している論文[1]とは異なります。
波長板のファスト軸およびスロー軸は、システムを透過する光パワーの測定値と、理論曲線1組とを比較することで確認します。これらの曲線を算出するのに必要なフレネル反射の式やその他の数式が提示されています。これらの曲線を計算するには反射面の屈折率も必要です。なお、複素屈折率の虚数部の符号は、好みの慣習に従って正でも負でもかまいません。どちらでもご使用いただけますが、符号により曲線についての解釈が異なることにはご留意ください。この動画では正の符号を用いています。
| Products Featured During Demonstration | ||||
| HeNe Laser | Quarter-Wave Plate | Unprotected Gold Mirror | Power Sensor | Power Meter |
| Optical Isolator (for HeNe) | Linear Polarizers | Kinematic Mirror Mount | SM1 Thread Adapter (for Power Sensor) | SM1 Lens Tube |
| V-Clamp Mount | Precision Rotation Mounts | Iris | Balldrivers | Quick-Release Lens Tube Adapter |
[1] Petre C t
t lin Logof
lin Logof tu, "Simple method for determining the fast axis of a wave plate," Opt. Eng. 44, 3316-3318 (2002).
tu, "Simple method for determining the fast axis of a wave plate," Opt. Eng. 44, 3316-3318 (2002).
最終更新日:2021年7月30日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 14 |
Visual Studio®プロジェクト作成とC#プログラミング: Kinesis® BBD300シリーズコントローラ
デバイスをリモート操作するためのソースコードを書く際の最大のハードルの1つとして、プログラムを開始し、接続するデバイスを初期化することがあげられるでしょう。こちらのKinesis®ソフトウェアパッケージのチュートリアル動画では、C#および.NET Frameworkを使用して新しいVisual Studio®プロジェクトを作成し、接続したデバイスを初期化する方法について手順を追って説明します。ここでは2軸ステージに接続したモーションコントローラBBD300シリーズを使用しています。動画では基本的な動作シーケンスがプログラムに追加され、コード実行のテストに使用されています。
デモでは新たにVisual Studioプロジェクトを作成し、必要なDLLを追加する方法について説明するところから始まります。ここの例では接続しているコントローラは1台のみです。コントローラのシャーシとチャンネルをそれぞれ初期化する必要があるため、プログラムは、2段階初期化プロセスが実行されるように書かれています。各チャンネルは接続したステージの1軸に接続します。
このデモでは、コントローラの2つのチャンネルのうちの1つが初期化されるため、2軸ステージは1方向に動作するようになります。動作コマンドでは、カスタムの速度と位置設定が規定されています。また動作シーケンス完了後、シャットダウンシーケンスを実行する指令も含まれています。メソッドによりエラーがスローされた場合に、プログラムに命令を供給するために、Try-Catchブロックがコードに追加されています。コマンドと位置のステータス情報がユーザに提供され、コンソール画面にステータスメッセージが示されます。
これらの手順は、同じコントローラとXYステージを使用する双方向ラスタスキャンを実行するプログラムのベースとして使用されています(下記動画参照)。
| Products Featured During Demonstration | |||
| Kinesis Software Package | Two-Axis Brushless DC Controller | XY Scanning Stage | Slide / Petri Dish Holder for Inverted Microscopes |
最終更新日:2021年11月17日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 15 |
偏光計を構築してストークスパラメータを測定し、偏光状態を特定する方法(Viewer Inspired)
偏光計は光の偏光状態を測定するのに用いる光学ツールで、直線偏光子、1/4波長板、パワーセンサ、およびパワーメータを用いて構築できます。この動画では手動式偏光計の2種類の構築方法(古典的な方法と、回転式波長板を使用した方法)を紹介し、両方の方法でレーザービームの偏光状態を測定しています。[1] どちらの方法でも、測定された偏光状態は4つのストークスパラメータを用いて記述されます。この動画では、直線偏光や円偏光などの異なる偏光状態とストークスパラメータとの関係についても解説しています。
この動画における左偏光と右偏光は、光の伝搬方向とは逆向きに光源方向を見たときに、時間とともに回転する偏光ベクトルの回転方向で定義しています。動画では、観察面を伝搬するビームに対して垂直な面に固定して示すことで、このルールを図解しています。ビームがこの観察面を通過すると、ビームの瞬間的な偏光ベクトルの先端がその面上で軌跡を描きます。その軌跡は時間の関数として描かれ、軌跡が描かれる方向は光の回転方向(左偏光または右偏光)に対応します。軌跡の形状は偏光楕円を表し、これは光の偏光状態を表す便利で一般的な方法です。偏光楕円とストークスパラメータの関係についても解説しています。
これらの偏光計を構築するのに用いた直線偏光子と波長板の透過軸は、撮影前にテーブルに対してアライメントされています。アライメント手順については下記のリンクから動画でご覧いただけます。
- 直線偏光子の軸をテーブルに対して垂直または平行にアライメントする方法
- 直線偏光子を入射面に対して45°にアライメントする方法
- 1/4波長板を使用して円偏光に変換する方法
- 波長板のファスト軸とスロー軸を区別する方法
| Products Featured During Demonstration | ||||
| HeNe Laser | Quarter-Wave Plate | Power Sensor | Power Meter | Fixed Position Retainer (Fork) |
| Optical Isolator (for HeNe) | Linear Polarizers | SM1 Thread Adapter (for Power Sensor) | SM1 Lens Tube | Optical Post Assemblies |
| V-Clamp Mount | Precision Rotation Mounts | Iris | Quick-Release Lens Tube Adapter | Balldrivers |
[1] Beth Schaefer, Edward Collett, Robert Smyth, Daniel Barrett, and Beth Fraher "Measuring the Stokes polarization parameters," Am. J. Phys. 75, 163-168 (2007).
最終更新日:2021年10月19日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 16 |
Visual Studio®とC#言語により双方向ラスタスキャンを実行する: Kinesis® BBD300シリーズコントローラ
XY電動ステージの利点は、リモート制御でラスタスキャンなどパターン化されたスキャンを特定の領域で実行できることです。動画では、BBD300シリーズモーターコントローラが接続した2軸ステージをステップ走査の双方向ラスタスキャンパターンで動かすためのプログラムを、当社のソフトウェアパッケージKinesis®利用して作成する方法を詳細に説明しています。プログラムは、C#、.NET framework、Visual Studio®の開発環境で書かれています。
こちらのチュートリアルは上の動画 Visual Studioプロジェクト作成とC#プログラミング: Kinesis BBD300シリーズコントローラの内容をベースに構築されています。様々なラスタスキャンパターンと手法の概要を説明した後、Visual Studioプロジェクト作成の動画で説明されている手順の簡単なデモがあります。これにはライブラリの参照、プロジェクトプラットフォームの設定、コントローラのシャーシと2つのチャンネルの初期化が含まれています。
移動には3つの要素が実行されます。1つは選択したステージ軸をホーム位置に戻し、もう1つは、ステージを特定の位置に移動させるために使用します。3つ目はジョグを実行し、ステージを特定の軸に沿って特定のステップサイズで移動させる方法です。ラスタスキャンは、最初にステージを初期位置に移動させ、その後、ステージのX軸およびY軸に沿ってジョグにより実行されます。コードをデバッグするためのサンプルが示されています。これにより、ステップ走査の双方向ラスタスキャンが正常に実行されるようになります。
| Products Featured During Demonstration | |||
| Kinesis Software Package | Two-Axis Brushless DC Controller | XY Scanning Stage | Slide / Petri Dish Holder for Inverted Microscopes |
最終更新日:2021年11月17日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 17 |
軸外放物面(OAP)ミラーをアライメントしてビームをコリメートする(Viewer Inspired)
軸外放物面(OAP)ミラーは発散光をコリメートするのによく使用されますが、ミラーのアライメントでは苦労することがあります。これはアライメント作業において調整しなければならない事項が複数あるためです。この動画では、アライメントの手順を個別のステップに分割して説明し、またミラーと光源を適切に配置するコツなども説明しています。さらに、適切なアライメントとミラーの形状や配置との関係について説明し、様々なミスアライメントによってビーム形状に生じる典型的な影響を観測用スクリーンでお見せしています。
動画では、光ファイバからの発散光をOAPミラーに入射し、その入射光とコリメートされた反射ビームが光学テーブル面と平行な面内を伝搬するようにするように調整しています。そのため、重要な最初のステップは、光源の高さとミラーマウントの取付け穴の中心を、必要とするコリメート光の高さに設定することです。次に、ミラーを回転させて反射光の面をテーブル面と平行になるようにし、続いてファイバの端面をミラーの焦点に移動させるという作業を、反復して行います。
| Key Components | Additional Products Featured During Demonstration | ||||
| Aluminum OAP Mirror | Post Collars | SMA-SMA Patch Cable | Viewing Screen (Smaller) | Spanner Wrench | |
| SM1-Threaded Adapter (for OAP Mirror) | Fiber-Coupled LED | Lens Mount | Viewing Screen (Larger) | Magnetic Button Clamps | |
| SM1-Threaded Mirror Mount | T-cube LED Driver | SM1-Threaded Fiber Adapter | Ruler | 1/4"-20 Cap Screw Kit | |
最終更新日:2021年12月14日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 18 |
Visual Studio®とC#プログラミングでカメラをセットアップし、画像を取得する
サイエンティフィックカメラをセットアップに組み込むときに、ハードウェアトリガ機能を用いて画像の取得と保存を自動で行うと便利です。その仕組みは、当社のサイエンティフィックカメラに付属するソフトウェア開発キット(SDK)を使用することで実現できます。ここでは、サイエンティフィックカメラの動作を制御するためのSDKの使い方について、C#で書かれたVisual Studio®のコンソールアプリケーション、およびサイエンティフィックカメラ、LED、LEDドライバ、PCなどのセットアップを使用して実演を行っています。
まずセットアップの一般的な概要説明を行い、次にLEDドライバがLEDに対してパルスを送信すると同時にTTL信号を出力する動作を5回行うようにシステムを構成する様子を見ていただきます。光源から光をパルス光とすることで試料の露光時間を制限することができます。TTL信号は画像取得と試料の光照射とを同期させるのに用いられます。TTLハードウェアトリガ信号はケーブルでカメラに接続します。
次に、何も書かれていないVisual Studioコンソールアプリケーションを開き、1行ごとに入力されるコードを説明します。このプログラムは、PCに接続されている使用可能な全てのカメラを検出できます。その中から1つのカメラを選択し、そのパラメータをこのセットアップ用として構成します。露光時間はLEDのパルス幅よりもわずかに短く設定し、ハードウェアトリガ信号を受信したときに1枚の画像が取得されるように指定します。各画像はビットマップファイルとして保存され、取得される画像は全部で5枚です。最後にプログラムを実行し、LEDの個別のパルスに対応した5枚の画像が取得されます。
DLLおよび参考資料のファイルパス
- プロジェクトのセットアップ中に追加されたDLL: C:\Program Files\Thorlabs\Scientific Imaging\Scientific Camera Support\Scientific Camera Interfaces
- カメラでサポートされている機能などについての詳細資料:C:\Program Files\Thorlabs\Scientific Imaging\Documentation\Scientific Camera Documents
最終更新日:2022年1月25日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 19 |
FiberBench上でのFiberPortのアライメント(Viewer Inspired)
この動画では、FiberBench上で2つのFiberPortをアライメントする手順を実演しています。この手順では、Zθネジなどの様々な調整ネジの機能が互いにカップリングしていることを考慮に入れています。3つのZθネジのいずれかを調整すると、レンズの向き(角度)とZ軸上の位置の両方が影響を受けます。3つのZθネジを1組のセットとして調整することで、最終的にレンズの角度方向またはZ軸上の位置のどちらか一方のみを調整するような動かし方が可能になります。
例えば、3つのZθネジを全く同じ量だけ同じ方向に動かすと、レンズはその向き(角度)は変えることなく、Z軸に沿って移動します。動画では、必要に応じてアライメント手順をカスタマイズできるように、これ以外の方法やその他の調整方法もご紹介しています。
FiberPortを互いにアライメントする前に、FiberPort内のレンズを事前に調整して、光ファイバからの光をコリメートしておく必要があります。FiberPortは予めアライメントしてから発送しますので、未使用のFiberPortをお使いになる場合にはこの手順は必要ありません。アライメントの手順としては、まずXY軸のアジャスタを調整し、次にZθアジャスタの調整に進みます。アライメント手順が複雑にならないように、Zθアジャスタの調整を始めたら、XYアジャスタの位置は変更しないことをお勧めします。
ファイバに結合する光パワーを計測し、それをアライメント状態のモニタとして使用します。しかし、調整したときにパワーが減少しても、必ずしも手順の失敗を示すものではないことにご留意ください。全体における最大値へ向かう途中の、局所的な極小値の場合があります。この動画では、アライメント状態の解釈や調査をするためのヒントを示すだけでなく、一貫した調整をするためのアドバイスも行っています。
| Key Components | Additional Products Featured | ||||
| FiberPorts | SM1 Thread Adapter (for the Power Sensor) | (FC/PC to FC/PC) | Fiber Connector Cleaner | ||
| Power Sensor | Adapter Cap | Single Mode Patch Cable (FC/PC to FC/APC) | |||
| Irises (Pillar Post and Flexure Clamping Base Used in Free-Standing Iris Assembly) | Power Meter | Multimode Patch Cable | Ruler | ||
最終更新日:2022年2月15日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 20 |
KF(QR)真空フランジの使い方
2つのKFフランジ付き真空用部品は、フランジ間のOリングを圧縮して接続します。この真空接続部のリークレートを最小化するには、フラットなフランジ面が滑らかでクリーンであること、またOリングに傷がなく柔軟性があることが必要です。この動画ではKFフランジ付き部品の接続方法と取外し方をご紹介し、合わせてこれらの真空フランジの取扱い、保守、組立てにおける要点などを解説します。KFフランジを使用している真空システムは、真空度のレベルとして一般に10-8 Torr (
KFフランジ付き部品を真空システムで使用するメリットは多々あります。例えば、ジェンダーレスである(オスメスの区別が無い)、サイズが標準化されている、接続や取り外しが容易である、比較的安価であるといったことがあげられます。これらのメリットの多くは、ガスケットとして機能するエラストマー製のOリングによるものです。
真空シールの性能は、フランジ表面とOリング両方の状態、Oリングへの圧縮力、Oリングの温度や使用方法の履歴など、いくつかの要因に依存します。Oリングは過剰な圧縮(>60%)や高温に曝されると、圧縮永久歪みが生じるのが早くなります。圧縮永久歪みとはOリングの形状に恒久的な変化が生じることを指し、これにはエラストマー素材が硬化することも含まれます。動画のようにOリングとフランジの表面を点検し、ダメージのある部品や硬化したOリングを交換することにより最適な性能が得られます。動画ではOリングに真空グリースを塗る方法のご紹介と、真空グリースを使用するかどうかを判断する際の考え方も解説しています。
| Products Featured During Demonstration | ||
| Wing Nut Clamp (KF25) | Blank Cap (KF25) | Nitrile Gloves |
| O-Ring and Carrier (KF25) | Elbow and Straight Pipes (KF25) | Solvent Dispenser and Wipes |
最終更新日: 2022年6月10日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 21 |
ベース、ポストホルダ、ポストなどを取り付ける際の注意点
光学系は通常、ポスト、ポストホルダ、ベースなどのコンポーネントを基礎にして構築されます。この基礎を設計して構築するには様々な方法があります。設計や構築の方法によっては振動の影響を受けやすくなったり、衝撃でミスアライメントが生じやすくなったりします。また、組立て方によっては偶発的にコンポーネントに損傷を与えかねません。
残念なことに様々な方法の効果は一般に全体を組み立ててからでないと分からないため、1つ1つの方法のメリットとデメリットを評価するのは困難であったり、時間がかかったりします。また、ポストやポストホルダ、ベースは慣れ親しんでいるコンポーネントであるため、ほかの方法があることすら考えないかもしれません。この動画では、当社で有益であると考え、またオプトメカニクス製品を初めて扱う方には良い出発点となるであろうと思われる方法をご紹介しています。
このデモンストレーションでは、一般的な光学システム構築用のコンポーネントに焦点をあて、設計やそれらを使った作業に長く携わってきた経験から得られたヒントなどもご紹介します。ベースのリリーフカット、ポストの貫通穴、ワッシャを使用することのメリットなど、気付かなかったかもしれないものの目的や使い方も明らかにします。機械的安定性を向上させるために選択すべきポストやポストホルダの高さに関するガイドラインや、ポストにキネマティックマウントを取り付ける際にマウントに損傷を与えないための方法などもご提示します。そのほか、比較的大きなコンポーネントを、2本のポストホルダ、2本のポスト、およびベースを使用して取り付ける方法もデモンストレーションしています。
こちらの動画では、ポストホルダを光学テーブル、ベース、あるいはブレッドボードにボルトで固定する際に、意図しない結果を回避し、また高さの調整範囲を維持する方法もご紹介しています。
| Products Featured During Demonstration | ||
| Posts | Compact Mirror Mount | 8-32 Hardware Kit Also Available: M4 Hardware Kit |
| Post Holder | Mirror Mount | 1/4"-20 Hardware Kit Also Available: M6 Hardware Kit |
| Mounting Base | Laser Diode Mount | Balldriver Caddy Kit, Imperial Also Available: Balldriver Caddy Kit, Metric |
最終更新日:2022年4月29日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 22 |
レーザースペックルを利用してビームの焦点を見つける方法
レンズがレンズチューブ、光学マウント、ケージプレートなどに取り付けられているとき、固定している部品内でのレンズの正確な位置がわからないため、ビームの焦点位置を正確に決められずにシステムのアライメントが困難になる場合があります。このような固定用部品からの焦点位置を見つける方法の一つとして、レーザースペックルを利用する方法があります。
この動画では、まずレンズチューブ内にマウントされたレンズの焦点を、レーザースペックルを利用して見つけます。各レンズの焦点位置を見つけたら、焦点とレンズチューブ外側の肩部分までの距離を測定します。
次に、2枚のマウントされたレンズの間に空のレンズチューブを挿入して、ケプラー式ビームエキスパンダを構築してみます。これらの2枚のマウントされたレンズ間に必要なレンズチューブの長さは、先ほど測定した焦点までの距離を使用して推定します。この方法により、初めに必要なレンズチューブの全長を推測し、次にビームの状態を繰返し測定して目的の長さが得られるまで調整を行うという、ビームエキスパンダ構築時の面倒な試行錯誤を避けることができます。
ここでは、透過型のすりガラス拡散板を使用してスペックルパターンを発生させています。拡散面(すりガラス面)が、ビームサイズが最小になる焦点の位置にあるときに、スペックルのサイズが最大になります。ビームは拡散面側に入射することを推奨しています。そうすることで、拡散板の光学的厚さを考慮せずに、焦点までの距離を直接測定することができます。ビームエキスパンダを構築できたら、シヤリング干渉計を使用して、拡大されたビームのコリメート状態を微調整します。
| Products Featured During Demonstration | |||
| Optical Diffuser | Compact Laser Module | Ø1" Lens Tubes | Dovetail Optical Rail |
| DIY Adapter (Diffuser to Slip-Ring Mount): Lens Tube Coupler and Retaining Ring | Adapter (Laser to Mount) | Adjustable Ø1" Lens Tubes | Optical Rail Carrier |
| Threaded Kinematic Mount | Slip-Ring Mount | Post Collar | |
| Plano-Convex Lenses | Fiber Storage Reel | Digital Calipers | Ruler |
| Shearing Interferometer | Viewing Screen | Retaining Ring Wrench | V-Groove Block |
最終更新日:2022年6月6日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 23 |
Python®による回転マウントとパワーメータの自動制御(Viewer Inspired)
Kinesis® K-Cube™モーターコントローラとパワーメータを自動制御するためのPythonスクリプトは、Visual Studio® Codeを用いて書かれています。このプログラムは回転マウントを180°回転させながらパワーメータで光パワーを測定することができ、可変光減衰器の特性を評価するときに必要になります。このコードは.NET Frameworkを用いて開発されたライブラリを使用するため、コードを実行するにはPython.NETのインストールが必要です。
こちらのチュートリアルでは、まずK-Cubeモーターコントローラ固有のコードを実装し、次にパワーメータのコードを実装します。両方のデバイスに必要なパッケージとクラスを特定し、また両方のデバイスの初期化手順やシャットダウンを完了するのに必要な手順を示します。さらにパワー読み取り値を取得する方法や、モータが動作中のコントローラのステータスを確認する方法などを説明します。Pythonスクリプトは、K-Cube部分のコードが完了した後と、プログラムが終了した後の2回実行されます。
K-Cubeモーターコントローラとパワーメータは、固定された互いに直交する2枚の直線偏光子の間に回転式1/2波長板を配置した光学系に対して、それを透過する光パワーを評価するように自動制御されます。1/2波長板を回転したとき、出射側の偏光子を透過する光の偏光方向は一定ですが、その光パワーは正弦波状に変化します。このプログラムによって、1/2波長板が固定されているマウントの回転角度の設定と、そのときの透過光パワーの測定が行われます。
動画のなかでVisual Studio Codeを用いて書かれたコードは、当社の公式GitHubアカウントのこちらからダウンロードいただけます。
最終更新日:2022年7月26日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 24 |
真空対応CF(コンフラット)フランジの使い方
超高真空レベル(10-8 Torr (1.33 x 10-8 mbar、1.33 x 10-8 hPa)より高真空)を実現するための接続方法として、2つのCF(ConFlat®)フランジの間に金属ガスケットを挟んで締め付ける方法があります。ここでは、その接続方法を、ファイバーフィードスルーの付いたCFフランジとCFフランジの付いたT字管のポートを使用して実演しています。真空封止の品質と真空システムを目標とする真空レベルまで排気するのに必要な時間は、ボルトが正しく締め付けられていることを確認すれば決まるというわけではありません。ここでは、良好な結果を得るのに役立つ、真空部品や真空システムを取扱うための方法もいくつかご紹介します。
ナイフエッジの損傷、ボルトの乱暴な締め方、ガスケットの再使用などは、すべてCFフランジによる真空接続部にリーク(漏れ)を発生させる可能性があります。動画で実演されている方法は、これらの要因によるリスクを軽減します。これらの要因はすべて金属ガスケットの展性(可鍛性)に関係しています。ガスケットは、ナイフエッジにおける傷などの幅の狭い急峻な形状を埋めるほどには柔らかくないため、ナイフエッジは新品のままの状態であることが重要です。ボルトを何回にも分けて徐々に締めていくのは、ガスケットの円周の厚さを均一に保つうえで効果的です。各ボルトを一度に締め付けると、ガスケットの厚さにばらつきが生じ、均一にすることが困難あるいは不可能になる場合があります。これは金属ガスケットの流動性に限界があるためであり、それによってガスケットとナイフエッジの間に隙間が生じる可能性が有ります。ガスケットは、常に新しいものを使用されることをお勧めします。前回の使用時に部分的にしか圧縮しなかった場合でも、再利用したときにはナイフエッジの輪郭に適合するのに十分な展性がない場合があります。これは圧縮により金属がひずみ硬化(加工硬化)するためです。
真空システムの接続部にリークがあると、リークチェックを行って問題箇所を特定したり、それを解決するために真空システムを再度開いたりなど、多くの時間を費やすことになりかねません。そのほか、チャンバ内部やチャンバに取り付けられたコンポーネントに破損や動作不良があると、生産的な作業が遅れる場合もあります。そのため、ファイバーフィードスルーの取扱い方などに関しても、特に注意すべき点についてご紹介しています。
ConFlat®はAgilent Technologies社の登録商標です。
| Products Featured During Demonstration | |||
| Optical Fiber Feedthrough | 1/4-Hard Copper Gaskets | Fiber Inspection Scope | Nitrile Gloves |
| UHV Fiber Patch Cable | Solvent Dispenser | Fiber Connector Cleaner | Wipes |
最終更新日:2022年9月21日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 25 |
空間光変調器(SLM)の位相遅延の校正方法
シリコン(Si)空間光変調器(SLM)の反射型液晶によって生じる位相遅延(位相変調)の大きさは、印加された制御電圧、周辺環境、入射光の特性など、さまざまな要因に依存します。製造者が印加電圧に対するSLMの位相遅延を校正するときは、通常、特定の動作条件下で、特定の波長のコリメート光を特定の角度で入射して行います。使用者のセットアップや動作条件は製造者の校正条件と大きく異なることがあるため、多くの場合、アプリケーションごとにSLMの位相遅延を再校正することは有意義です。
この動画では、入射光の直線偏光の状態に影響を与えずに位相変調できるように設計された反射型SLMの位相遅延を、干渉によって校正する方法[1]をご紹介します。校正用のセットアップに必要なものは、SMLの他にはコリメートされた直線偏光の入射光とカメラだけです。
SLMの位相遅延のパターンはグレースケール値で表すのが一般的で、グレーの各濃淡が特定の位相遅延を表します。校正することで、現在の動作条件下における、各グレースケール値に対応する位相遅延が決定されます。この校正方法では、SLMのパネルの半分に均一な位相遅延が生じるようなパターンを適用します。この半分はミラー側になり、これにより反射光が得られます。残りの半分にはバイナリ位相回折格子となるようなパターンを適用し、それにより回折ビームが得られます。反射ビームと -1次回折ビームが重なり合って干渉縞が生成され、校正中はそれをモニタします。SLMのミラー側に印加される電圧を全範囲にわたって変化させると、印加電圧の変化に伴って干渉縞がシフトします。干渉縞のシフト量は位相遅延の変化量に直接関係します。
この動画に付随するもう一つの動画では、液晶層の光学特性に関する追加情報をご紹介しています。そこでは印加電圧が液晶層の屈折率に与える効果や、直線偏光の向きが異なる場合における液晶層の効果などもご説明しています。直線偏光の向きが、SLMの光軸と呼ばれる液晶層内の分子の回転面と平行でない場合には、予期しない結果が得られることになりますのでご注意ください。
[1] José Luis Martínez Fuentes, et al., "Interferometric method for phase calibration in liquid crystal spatial light modulators using a self-generated diffraction-grating," Opt. Express. 24, 14159 - 14171 (2016).
最終更新日:2023年11月29日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 26 |
シヤリングプレートコリメーションテスタを用いてレーザをコリメートする方法(Viewer Inspired)
シヤリングプレートコリメーションテスタは、光路に挿入しやすいコンパクトなシヤリング干渉計です。光路に設置することで、レーザービームのコリメート状態を評価し、かつ最適化するために使用することができます。この動画では、このデバイスの使用方法やトラブルシューティングの要領、特定のビームのコリメート状態を試験する際にアプローチの適切性を判断するための指針などをご紹介しています。
ここではコリメート用レンズとしてアクロマティック複レンズを使用していますが、そのレンズの位置を調整している間、デバイスはビーム内に納まっています。デバイス上部にあるすりガラス拡散板上に見える干渉縞は、ビームの状態(集束、発散、またはコリメート状態)を示します。
この測定方法では、光が十分にコヒーレントであること、波面収差が小さいこと、シヤリングプレートの厚さがビーム径に対して適切であることなどが求められます。また、ビームがコリメート状態を維持できる距離は無限ではないため、デバイスはコリメート光のビームのウェストからおよそ1レイリー長の範囲内に設置する必要があります。
干渉縞が見えない場合や干渉縞と判断するのが難しい場合に、問題を解決するためのアイデア等をご紹介しています。具体的には、より薄いシヤリングプレートを使用する、レンズの位置を調整する、デバイス上部に拡大ビュアーを追加する、といった解決策を示しています。また、波面収差が非常に大きい場合やコヒーレンス長が不十分な場合には、ビームのコリメーションを試験して最適化するために別の方法が必要であることも示しています。
最終更新日: 2023年3月22日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 27 |
偏波保持ファイバに結合する光の偏光方向をアライメントする方法
偏波保持(PM)ファイバでは、PMファイバの2つ軸のうちの1つに対して偏光方向が適切にアライメントされた直線偏光だけが、その偏光状態を維持することができます。そのため、偏波保持ファイバに光を結合するためのセットアップでは、しばしば直線偏光子と入射光の偏光方向を回転させるための何らかの手段が使用されます。この動画では、直線偏光の入射光をアライメントするための方法を2つご紹介しています。1つ目の方法では偏光計を使用し、2つ目の方法では光パワーセンサの前に直線偏光子を置いてパワーを測定します。どちらの方法もファイバの複屈折性をスムーズに増加または減少させる必要があります。そのために、この動画ではファイバを加熱または冷却しています。
光を偏波保持ファイバに結合する場合、まず最大の結合効率を得られるようにシステムを調整することが重要です(以前ご紹介したファイバーベンチやファイバーコリメータの調整と同様です)。次に、動画でご紹介している2つの方法のうちのどちらかで、入射光が直線偏光であること、およびその偏光方向が偏波保持ファイバのスロー軸またはファスト軸に対して平行になっていることを確実にします。このようにアライメントすると、光はファイバの1つの軸だけに沿って進むため、偏波保持ファイバは入射光の偏光状態を維持することができます。
偏光計を使用する方法と偏光子を使用する方法の両方を用いて、偏波保持ファイバからの出射光を測定します。この動画では、より適切にアライメントされると、偏光計のデータがポアンカレ球の赤道上の点の周りでより小さな円の軌跡を描くことが示されます。それらのデータは、適切に配向された直線偏光子を透過した光パワーの測定値と並べて表示され、比較することができます。より適切にアライメントされると、光パワーの振動の振幅がより小さくなります。また、動画では偏波保持ファイバとそれに関連するポアンカレ球上での特性についても簡単に説明しています。
光と偏波保持ファイバの相互作用についての詳細はこちらをご覧ください。
最終更新日:2023年5月1日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 28 |
ヘリオットセルのセットアップと構成(Viewer Inspired)
ヘリオットセル内では、光が2つの凹面ミラー間で何度も反射を繰り返します。反射されたビームは2つのミラー間をさまざまな角度で伝播し、さまざまな経路をたどってミラー上に直線形、楕円形、あるいは円形の光のスポットのパターンを形成します。セルにビームを入射/出射させるために、一般にどちらか一方または両方のミラーに穴(中央またはエッジ近傍)が開いています。ヘリオットセルは、長い光路長をコンパクトなスペース内に折りたたむことができるという利点があるため、様々な用途で用いられています。ガス吸収分光法は良く知られている用途ですが、これはビームがサンプル体積内を通過するたびに、測定データの信号対雑音(S/N)比が増大するためです。
この動画のセットアップは、開始時点では粗くアライメントされた状態です。セットアップの一方のミラーはエッジ近傍に1つの穴があり、もう一方のミラーには穴がありません。2つのミラーの焦点距離は同じです。偏光無依存型ビームスプリッタと2つのアイリスを使用して、ミラーの面が互いに平行で、かつテーブルのネジ穴の配列に対して垂直になるように調整します。この作業が完了したらミラーの角度調整は完了です。次に、入射ビームの向きとセルの長さを変えて、ミラー上でさまざまな反射パターンを得る方法をご紹介します。
入射ビームの角度とミラー間の距離は、どちらもビームがセルから出射するまでに反射する回数に影響します。特殊なケースとして、2つのミラーの焦点距離が等しく、かつミラー間の距離が焦点距離と同じ場合があります。このような構成にした場合は、入射ビームの向きに関わらず、ビームはセル内を6回通過します。このミラー間隔の状態は、入射ビームのピッチ角とヨー角、およびX軸とY軸の位置を変えたときの影響を見るのに使用します。また初期設定として、入射ビームがセルの光軸に対して平行になるようにアライメントします。次に、ビームのセル通過回数が増えるようにセルの長さを調整します。この動画では、入射ビームの向きをさらに調整して、直線形、楕円形、および円形の反射パターンを生成しています。
参考文献:
D. Herriott et al., Appl. Opt. 3, 523-526 (1964).
C.G.Tarsitano et al., Appl. Opt. 46, 6923-6935 (2007).
最終更新日:2023年7月14日
本セクションへのリンクのコピーはこちらから(右クリックしてください) | 29 |
LEDからの出力光をコリメートする方法
LEDほか広帯域のインコヒーレント光源からの光のコリメートは意外にも困難な場合があります。エミッタのサイズ、コリメートレンズの焦点距離と開口数(NA)はすべて、コリメートビームの特性に影響を及ぼします。また、レンズが適切な位置にあることを見極めるのも難しい場合があります。この動画では、NAと焦点距離の異なる2つのレンズを使用して、いくつかのコリメーションの手法のデモを行います。また、エミッタの像ほかコリメートレンズによって得られるビームの典型的な特性についても探っています。
コリメート光の2つの重要な特性は、発散角と光パワーです。デモでご覧いただけるように、2つのレンズの直径が同じ場合、焦点距離が小さい方がNAが大きいため、より多くの光を集めることができます。しかしその代償としてコリメートビームの発散角が大きくなります。発散角は発光エミッタの物理的なサイズにも影響を受けます。同じレンズを使うことを仮定すると、エミッタが大きいほどコリメートビームの発散角は大きくなります。
発散角が大きくなるということは、ビームの放射照度(単位面積あたりの光パワー)が、レンズからの距離が遠くなるほど小さくなることを意味します。そのほかにも、コリメート領域が短くなります。コリメート領域は、エミッタ全体からの光線が重なるビームの部分と説明することができ、通常はレンズの近くにあります。 レンズからの距離が離れるにつれて、発散により光線がそれぞれの起点により異なる光線束に分離し、エミッタの像が現れます。像が現れることは、薄型レンズの方程式では予測できないため想定外の場合もあり、またご用途によっては予期しないアーティファクトが発生する場合があります。
最終更新日:2024年1月12日
本セクションへのリンクをコピーするには、こちらを右クリックしてください。 | 30 |
追尾機能を備えた太陽撮像望遠鏡の構築
太陽のイメージングは人にも装置にも危険が伴いますが、望遠鏡を改造して光減衰器を組み込み、画像の光強度を安全なレベルまで下げることは可能です。さらにモータやソフトウェア制御を追加し、太陽望遠鏡の方位角と高度を自動調整して、空を移動する太陽を連続的に追尾することも可能です。この動画では、屈折式の太陽撮像望遠鏡を設計・製作してその様子をお見せします。望遠鏡の撮像装置にはカメラを使用し、モータの制御はPythonコードで行います。Pythonコードとその使い方の詳細は、当社のGitHubページからダウンロードいただけます。
望遠鏡の設計は、カメラのCMOSセンサの寸法、飽和露光量、および応答性によって制約されます。レンズの焦点距離は、センサの受光面の適切な範囲内に最大の像が得られるように選択します。この焦点距離でレンズとカメラの間隔が決まります。光の減衰量を最適化するには、センサの飽和露光量より極めて低い光強度が得られる減衰量を計算し、まずそれを適用します。次にカメラの露光時間を10ミリ秒未満に短縮できるまで、減衰量を徐々に小さくします。
追尾機能は2つの電動回転ステージを用いて実装しますが、それらのステージは3Dプリントで作成されたカスタムブラケットで直交するように接続します。カスタムブラケットの設計ファイルはこちらからダウンロードいただけます。室内で試験と大まかなアライメント調整を行った後、望遠鏡を外に持ち出して、太陽のイメージングと追尾機能の性能をお見せします。
最終更新日:2024年4月4日
本セクションへのリンクをコピーするには、こちらを右クリックしてください。 | 31 |
光の透過率とブリュースター角の入射角依存性
ガラスの表面での光の反射率は4%と仮定するのが一般的です。この経験則は垂直入射に近い場合は適用できますが、このような近似はすべての入射角に対して適切というわけではありません。また、入射光の偏光状態が反射光や透過光のパワーに与える影響についての情報もありません。このデモンストレーションでは、回転するガラスウィンドウからの反射光と透過光を観察し、フレネルの式によるモデルから得られる結果と比較しています。4%ルールの限界について調べ、反射率と透過率の偏光依存性についても探ります。
まずs偏光、次にp偏光の入射光を回転するウィンドウに入射し、光の反射率と透過率が入射光の偏光状態に依存することを明らかにします。(s偏光は入射面に垂直な直線偏光であり、p偏光は平行な直線偏光です)。そして入射したp偏光がすべて透過し、したがってs偏光のみが反射する入射角があることを示します。これはブリュースター角と呼ばれ、このデモンストレーションでは光がブリュースター角で入射するようにウィンドウの向きを調整する方法を実演しています。
また、s偏光とp偏光に対する透過率と反射率の値がわかっている場合は、入射面に対して45°の方向に直線偏光している光を用いて、非偏光に対する透過率や反射率を予測できることも示しています。
最終更新日:2024年5月7日
本セクションへのリンクをコピーするには、こちらを右クリックしてください。 | 32 |
| Posted Comments: | |
Anand P
(posted 2022-04-20 15:27:04.123) Hi!
In "Insights" article named "Photonics", there is statement, "For example, a laser pointer that outputs 1 mW of red (640 nm) light provides 3 x 10^16 photons/s"
However, 1mW beam of 640 nm will produce ~3 x 10^15 photons/s. lmorgus
(posted 2022-04-20 04:57:03.0) Thank you very much, Anand, for your feedback and catching our typo! We have now corrected the value on the What is Photonics Insight.
For those who are curious, the energy (E) in a single photon is equal to the product of Planck's constant (h = 6.62 x 10^-34 m^2 kg / s) and the speed of light (c = 3 x 10^8 m / s) divided by the wavelength of light (L = 640 x 10^-9 m): E = h*c/L = 3.1 x 10^-19 J / photon at 640 nm. A 1 mW power (P) provides 10^-3 J / s, so there are P / E ≈ 3 x 10^15 photons / s provided by the beam. Tariq Khwaja
(posted 2021-09-15 15:50:03.287) Assalamualaikum. Sorry, please retract my previous comment. I was mistaken in that I did not realize the error function is a cumulative of the Gaussian. i.e. the calculations differ for it. Marshall Scott
(posted 2020-02-24 18:25:14.367) Does NA provide a good estimate of beam divergence from a single mode fiber?
It's a good tip, but you're comparing a 1/e^2 beam radius to something closer to a 99% beam radius (NA), and that hurts my soul. llamb
(posted 2020-02-28 01:54:14.0) Hello Marshall, thank you for your feedback. As you are probably aware, there are different ways to define a Gaussian beam's spot size, including but not limited to the full width half max (FWHM), the radius at which the intensity drops to 1/e2 times the peak intensity, and the radius enclosing 99% of the power. The definition of the outer radius of a Gaussian beam must be chosen to suit the application. This particular Insight resulted from someone in the lab accidentally using the fiber's NA to estimate the 1/e2 beam size after a collimating lens, and our desire to prevent others from making the same mistake. For collimating light from and focusing light into a single mode fiber, using the 1/e2 point to define spot size appeared to be the most applicable, since the fiber's mode field diameter is defined in terms of the 1/e2 point. We provided a direct comparison between the divergence angles corresponding to this radius and those calculated from the NA to emphasize the significant difference in the two results, which if unexpected could lead to errors. To your point, if the radius enclosing 99% of the beam's power were drawn, this radius would be a factor of ~1.5 times larger than the radius to the 1/e2 point. Applying this case to the Insight example, the divergence angle in the far field would be 8.3°, which is even larger than the angle calculated using the ray optics NA approach. This is another crucial point to consider when choosing the collimating/focusing lens and we will be using your feedback to expand our collection of Insights in the near future. |
 Products Home
Products Home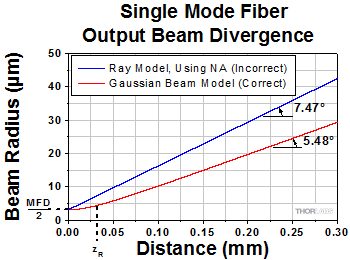

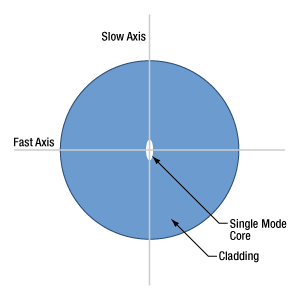
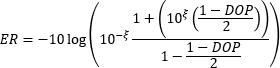
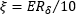 ,
,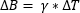
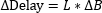
 Insights-まとめ集
Insights-まとめ集