パルスの歪み:方形パルスの形状を維持する方法

Please Wait
Click to Enlarge
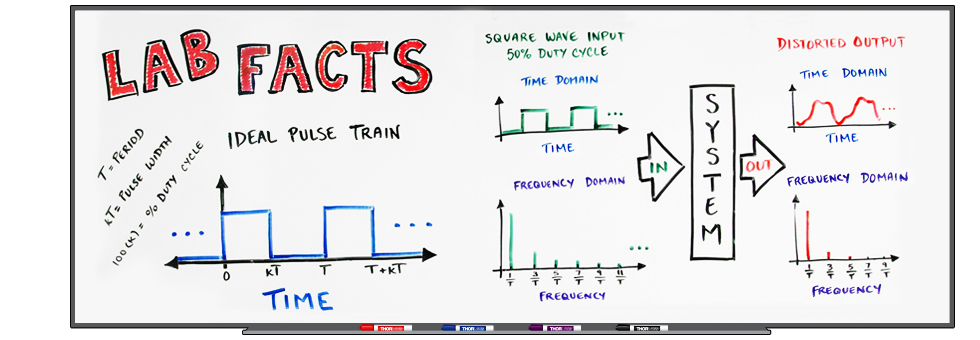
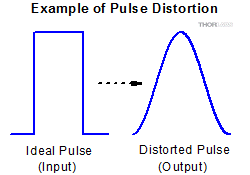
Figure 1.1 パルス歪みの極端な例。システムの応答が遅いため、入力パルスに対して出力パルスの形状は歪んでいます。
方形パルスの出力に必要な3 dBシステム帯域幅とは?
パルスの歪みとは理想的なパルス形状からの変形を意味し、システムが入力信号の振幅変動に対して十分な速度で応答できないとき、その出力信号に現れます。システムによるパルス出力の歪みは、システムの帯域幅が入力信号の帯域幅を処理するのに十分でないときに発生すると考えられます。この現象は入力信号が繰り返し周波数の高い矩形波あるいは方形パルス列の場合に頻繁に見られます。歪んだ方形パルスは、しばしば Figure 1.1 のように丸みを帯びた形状になります。
パルスの歪みは、入力信号をスケーリングした信号を出力するあらゆるシステムにおいて懸念すべきものです。例えば、ファンクションジェネレータからの入力信号で半導体レーザに電流信号を供給する半導体レーザードライバを含むシステムを考えてみます。そのドライバは、ファンクションジェネレータからの入力信号をそのまま反映した電流信号を出力することが期待されます。入力信号の周波数がシステムの仕様帯域幅内のときは、一般にシステムは出力信号の歪みを最小に抑えるよう設計されており、その周波数領域ではシステム応答は最適化されています。
しかし、歪みの無いパルスを出力できる応答の速いシステムを使用することは、常に可能というわけではなく、または望ましくない場合もあります。入力信号の帯域幅がシステムの3 dB帯域幅より広い場合、出力信号のパルスに歪みが生じることが予想されます。
こちらの実験では、3 dBカットオフ周波数が750 kHzのレーザーシステムに様々な帯域幅の方形パルス列を入力してみました。得られた出力信号の歪みを2つのアプローチで解析しています。1つは入力信号と出力信号を周波数成分ごとに調べる方法です。もう1つは入力パルスと出力パルスの形状を比較する方法です。これらのアプローチは次の作業に適用されています。
- 入力信号として異なる方形パルス列を使用したときの出力信号のパルス歪みの調査
- 3 dBシステムカットオフ周波数と入力信号の繰り返し周波数に関する9倍ルールを適用したときのパルス品質の調査
- 方形とされている出力信号のパルス形状を数値的に評価する方法の開発
方形パルス列とは?
Click to Enlarge
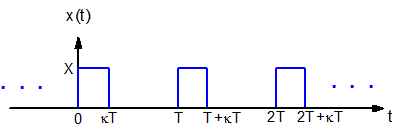
Figure 1.2 時間(t)の関数として表された理想的な方形パルス列。周期(T)、デューティーサイクル(κ)、およびハイレベルの値(X)が記載されています。
方形の入力パルス列
方形パルス列信号では、トップハットの形状をした方形パルスが繰り返されます。このパルス形状は信号レベルが最小値から最大値に遷移し、最大値で一定の時間とどまり、そして最小値に遷移することで生成されます。その様子を Figure 1.2 に示しています。
理想的な方形パルスでは2つの信号レベル間の切り替え時間はゼロで、瞬間的に遷移します。方形パルスは周期(T)と呼ばれる一定の時間間隔で繰り返されます。パルス幅はパルスが最大値(ハイレベル)にとどまる時間で表され、デューティーサイクル(κ)はパルスが最大値にとどまる時間の周期に対する割合です。方形パルス列のデューティーサイクルは0~1の間の数値で、これはパルス幅を周期で割ることで求められます。デューティーサイクルはしばしば周期に対する百分率(%)で表されます。Figure 1.2 では、振幅の最大値(ハイレベル)はX、最小値(ローレベル)は0になっています。
もし Figure 1.2 の波形を周波数の関数として表示しようとすると、周波数軸を無限大まで拡大する必要があります。短時間での遷移を実現するには高い周波数成分が必要になり、理想的な方形パルスを作るには無限の周波数成分が必要になります。一般にシャープで幅の狭い周期信号を作るには、周期の逆数で与えられる基本周波数よりも高周波側のたくさんの周波数成分が必要です。
1
システムの3 dBカットオフ周波数はなぜ重要か?
システム帯域幅が制限されることによる影響
システムの帯域幅はシステムが入力信号の変化にどれだけ迅速に応答できるかの尺度であり、これはシステムがサポートできる最大周波数の指標とも言えます。しかしシステムの帯域幅が入力信号の帯域幅より狭いことは稀ではありません。このようなミスマッチが起きたとき、入力信号の高周波数成分は出力信号には含まれず、その結果としてパルスに歪みが生じます。
方形パルス列から高周波数成分が除去された場合、パルスの鋭いコーナー部分に丸みが生じ、信号のローレベルとハイレベル間の遷移に要する時間が長くなります。高周波数成分を十分に除去していくと、入力された方形パルス列を正弦波に変換することができます。
3 dBカットオフ周波数
システムの帯域幅は、システムがある程度の応答をする絶対最大周波数ではなく、しばしば3 dB帯域幅によって表されます。一般に3 dB帯域幅で表される理由としては、最大周波数を求めるのが難しい場合があること、また3 dB帯域幅外の周波数成分はシステムの性能にあまり寄与しないことなどが上げられます。3 dBカットオフ周波数より高い周波数成分はシステムで大きく減衰するため、3 dBカットオフ周波数より低い周波数の入力信号成分のみで構成される出力信号を考えれば済むことになり、便利なこともよくあります。しかし、3 dBカットオフ周波数より高い周波数成分も出力信号に寄与していることには留意しておく必要があります。3 dBカットオフ周波数については、出力信号と入力信号の周波数成分がどのように異なるかを推定するための一般的な参考値として使用することをお勧めします。
2
実験のセットアップ
実験のセットアップ
実験のセットアップはページ上部の図でご覧いただけます。ファンクションジェネレータからの方形パルス列は、ピグテール付き半導体レーザ用のマウント付き電流/温度コントローラCLD1010LPに入力されます。ユーザが定めた定電流成分を含むコントローラからの出力電流は、コントローラに取り付けられたピグテール付き半導体レーザに供給されます。半導体レーザに供給される定電流成分の大きさは、全電流が常にレーザの発振閾値を超えるように設定されています。ドライバから供給される変調電流により、半導体レーザは変調された光信号を出力します。
この光信号は80 MHzファンクションジェネレータに接続されている1 GHz FC/PCファイバ入力フォトディテクタDET02AFCで受信されます。レポートに記載された手順に従って、システムの3 dBカットオフ周波数は750 kHzと求められました。ファンクションジェネレータからの方形パルス列と検出された光信号とは、信号の周波数成分とパルス形状の両方を解析して比較しました。
3
繰り返し周波数のパルス歪みへの影響は?

Click to Enlarge
Figure 1.3 入力する矩形波の繰り返し周波数を3 dBカットオフ周波数750 kHzまで変化させて測定した出力波形†です。繰り返し周波数が83.3 kHz(濃い赤)のときは、カットオフ周波数が繰り返し周波数よりも9倍大きく、出力信号は入力信号を適度に再現しています。
†立ち上がりエッジのオーバーシュートと立ち下がりエッジのアンダーシュートはアーティファクトで、システム内のコンポーネント間のインピーダンス不整合が原因である可能性があります。
入力矩形波の繰り返し周波数を大きくした場合
矩形波はデューティーサイクルが50%の方形パルス列です。従って、矩形波のパルス幅*は常に周期の半分になります。この周期は繰り返し周波数を変えることで調整できます。これは周期が繰り返し周波数の逆数で与えられるためです。
様々な繰り返し周波数の矩形波を上記のシステムに入力しました。測定された出力パルスの一部を Figure 1.3 に示しますが、これから繰り返し周波数が3 dBカットオフ周波数に近づくにつれてパルス歪みが大きくなることが分かります。
繰り返し周波数が増加するとパルス幅は狭くなりますが、出力信号のローレベルからハイレベルへの遷移に要する時間は変化しません。その結果、繰り返し周波数が増加すると信号におけるローレベルとハイレベル間の遷移時間の割合が増加し、それに伴ってパルスのスロープは垂直の状態から次第に傾斜するようになります。またパルスのハイレベルの部分も、繰り返し周波数が増加すると平坦ではなくなります。極端な例として、繰り返し周波数が3 dB帯域幅と同じときには、出力信号は正弦波によく似た形になります。
3 dBカットオフ周波数と繰り返し周波数の関係を調べるうえで有効な方法は、理想的な矩形波を次のようにフーリエ級数展開してみることです。
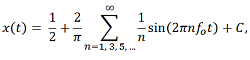
この式は矩形波が無限の正弦波の和として表せることを示しています。定数(C)は矩形波の振幅の平均値をシフトさせますが、パルスの形状には影響しません。入力信号の繰り返し周波数は、級数展開の1次の項(n = 1)の周波数に等しくなっています。この周波数は基本周波数(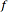 o)と呼ばれます。矩形波の高次周波数成分は、基本周波数の奇数倍(n = 3, 5, ...)の周波数を有します。
o)と呼ばれます。矩形波の高次周波数成分は、基本周波数の奇数倍(n = 3, 5, ...)の周波数を有します。
この級数展開を踏まえて測定結果を考えると、以下のような興味深いことが明らかになります。
- 繰り返し周波数を増加すると各項の周波数も増加する。
- 1次の項(n = 1)は振幅が最大の正弦波である。
実験中に繰り返し周波数を増加させたことは、3 dBカットオフ周波数よりも低い周波数の入力信号成分が少なくなることにつながります。出力信号のパルス歪みは、この閾値よりも高い周波数の信号成分が大きく減衰することが要因ということになります。3 dBカットオフ周波数よりも低い周波数の項が少なくなると、1次の項の正弦波が占める割合が大きくなり、出力波形は徐々に正弦波に似てきてきます。 繰り返し周波数が3 dBカットオフ周波数と一致したときには、3 dBカットオフ周波数以下の周波数成分は1次の項のみになります。
*信号がハイレベルにとどまる時間
4
9倍帯域幅ルールとは?
矩形波の9倍帯域幅ルール
出力パルスの歪みは、システム帯域幅が入力信号の帯域幅に一致する、あるいはそれよりも大きいときには最小化されます。それが実現できない場合、あるいは実用的でない場合には、出力信号が入力信号の矩形波を適切に表示するうえで必要なシステムの最小帯域幅を求めることは有益です。9倍ルールは多くの用途において優れたガイドラインとなります。このルールでは、システムの3 dB帯域幅は、測定しようとする矩形波の繰り返し周波数の9倍以上あるべきであるとしています。矩形波のデューティーサイクルは50%ですが、このルールはデューティーサイクルが50%近辺の信号にも適用できます。しかし、デューティーサイクルが50%から大きく増減すると出力信号の歪みは大きくなります。出力パルスが理想的な条件下で矩形波と識別できるためには、システムの3 dB帯域幅は入力信号の繰り返し周波数の3倍以上必要と考えられます。
このガイドラインはフーリエ級数展開に基づいています。システムの3 dBカットオフ周波数が繰り返し周波数の9倍の場合、入力信号にはカットオフ周波数よりも低周波側のゼロにならない周波数成分が5つ含まれることになります。 Figure 1.3 の83.3 kHzのグラフはその状態に対応しており、理想的な矩形波に対して実用上妥当なパルスの形状を示しています。システムの3 dB帯域幅が入力信号の繰り返し周波数の3倍の場合、システムの3 dBカットオフ周波数よりも低い周波数成分は2つです。これは繰り返し周波数が250 kHzの場合に該当し、そのパルスは何とか方形だと識別できる形状をしています。システムの3 dBカットオフ周波数と繰り返し周波数が等しい場合、1次の項の周波数のみがシステムの3 dB帯域幅内にあることになります。750 kHzの曲線は、このような条件では正弦波が出力されることを示しています。次のセクションではデューティーサイクルが20%になったときの出力パルスの歪みについて解説します。
5
パルスの形状と要求されるシステム帯域幅に対するデューティーサイクルの影響は?
Click to Enlarge
Figure 1.4 デューティーサイクル20%の周期的な方形パルス列の入力に対する出力波形。繰り返し周波数はグラフ上に表記。 繰り返し周波数を固定してデューティーサイクルを小さくしたときのパルス形状への影響は、上の図の83.3 kHzのグラフと Figure 1.3 のそれとを比較することで見ることができます。
方形パルス列のデューティーサイクルの低減
入力する方形パルス列の繰り返し周波数を固定してデューティーサイクルを小さくした場合、パルス幅が小さくなります*。この時もシステム帯域幅が信号帯域幅より狭いと出力信号のパルス歪みが大きくなります。またローレベルからハイレベルへの遷移時間のパルス幅に対する割合が大きくなり、これもパルスの歪みが大きくなる要因になります。もう一つの結論として、信号がハイレベルで安定している時間が短くなってしまうことが上げられます。
Figure 1.4 は、入力信号のデューティーサイクルが20%のときに実験システムから出力されたパルスの測定例です。システム帯域幅が繰り返し周波数83.3 kHzの約9倍のとき、パルスの形状は何とか方形と識別できる程度です。繰り返し周波数が200 kHzになると、システム帯域幅は繰り返し周波数の3倍以上ですが、出力パルスは正弦波の形状になっています。これはデューティーサイクルが50%の場合とは異なります。50%の場合は、繰り返し周波数がより高い250 kHzのときでもパルスは何とか方形と識別できる状態でした。
*信号がハイレベルにとどまる時間
6
入力信号と出力信号のデューディーサイクルを比較すると?
Click to Enlarge
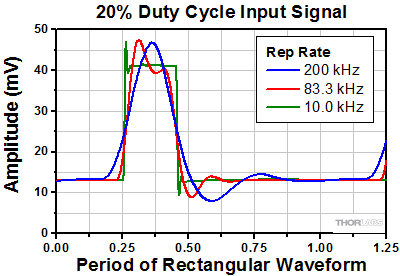
Figure 1.5 入力と出力のパルス列のデューティーサイクルは、繰り返し周波数がシステム帯域幅の750 kHzに近づくにつれて変化します。高次の周波数成分が減衰するほど、出力信号のデューティーサイクルは50%に近づきます。
入力および出力パルス列のデューティーサイクル
デューティーサイクルが50%ではない入力信号の繰り返し周波数を増加すると、出力パルスに歪みが生じるとともに、出力信号のデューティーサイクルが入力信号に比べてより50%に近づいていきます。前述の750 kHzのシステムを用いた測定結果を Figure 1.5 に示しますが、これからその傾向を見ることができます。200~300 kHzの繰り返し周波数では、入力信号と出力信号のデューティーサイクルは良く一致しています。入力信号と出力信号のデューティーサイクルが異なるようになるのは、システム帯域幅が繰り返し周波数の3~4倍くらいからです。それよりも高い繰り返し周波数においては、出力信号のデューティーサイクルが50%に収斂していきます。
これは、入力信号の基本周波数成分が正弦波であることによります。正弦波のデューティーサイクルは50%で、要求されるデューティーサイクルの波形を得るにはより高い周波数成分が必要になります。繰り返し周波数を増加させると、システムの3 dBカットオフ周波数よりも高い周波数の入力信号成分が増加します。これらの高い周波数成分はシステムによって減衰してしまうため、出力信号では基本周波数成分が支配的になります。
7
パルス歪みを数値的に評価する方法は?
Click to Enlarge
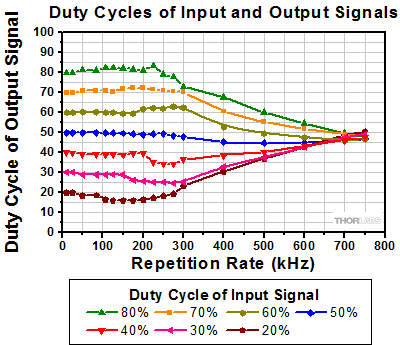
Figure 1.6 矩形波(緑)と正弦波(青)のパルス幅はともに0.5Tです。点線部分は、ローレベルからハイレベルへの遷移を表しています。矩形波では、遷移時間は無限に短く、各レベルでの滞在時間は0.5Tです。正弦波はその正反対です
品質係数の定義
品質係数によるアプローチは、方形とされる出力パルスのパルス歪みを予測したり、評価したりするために開発されました。これはフーリエ解析の原理を視覚化する方法で、フーリエ変換やフーリエ級数といった計算や、同様の解析作業を必要としません。この方法では、測定されたパルスの形状と、理想的な方形パルスの形状との類似性を評価します。これは、測定されたパルスの立ち上がり時間と、それに近似する理想的なパルスの幅を比較することによって行われます。
Figure 1.6 では、理想的な矩形波パルスを緑色で、フーリエ級数展開における1次の項の正弦波を青色で示しています。点線はそれらの立ち上がりエッジです。品質係数が最大値の1のときは理想的な方形のパルスを表し、振幅の最小値から最大値までの遷移時間が無いことを示しています。品質係数がゼロのパルスの遷移時間は、理想的なパルスのパルス幅と同じになります。例えば、Figure 1.6 の青いパルスの遷移時間0.5Tは理想的なパルスの幅と等しいため、品質係数はゼロです。
実際の信号では、信号ノイズや不安定性により、遷移時間を正確に測定するのは難しい場合があります。そのため、通常は、振幅の最小値のわずかに上の位置から、最大値のわずかに下の位置まで変化するのに要する時間を測定します。立ち上がりエッジにおいて、振幅の10%と90%の位置で測定するのが一般的です。品質係数 (Γ)は、このパルスの立ち上がり時間( r)の測定値と、理想的な方形パルスの幅(W)を用いて、次の式で求められます。
r)の測定値と、理想的な方形パルスの幅(W)を用いて、次の式で求められます。

この近似式の求め方と、50%以上のデューディーサイクルでは推奨されない理由についてはレポートをご覧ください。
8
入力信号のデューティーサイクルが品質係数に与える影響は?
Click to Enlarge
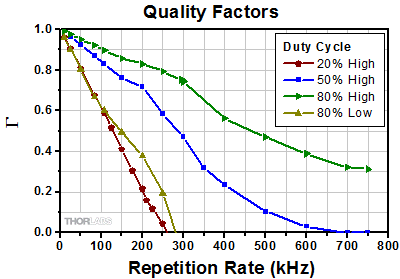
Figure 1.7 周期的な方形パルス列を3 dBカットオフ周波数750 kHzのシステムに入力し、出力波形の品質係数*を求めました。デューティーサイクルが80%の2本の曲線は、理想的なハイレベルの幅とローレベルの幅を用いて計算した品質係数です。データポイントは見やすくするために線で結んでいます。
*「High」および「Low」の記載は、品質係数を計算する際に、理想的な方形パルスのハイレベルの幅を用いているか、あるいはローレベルの幅を用いているかを示しています。
品質係数の測定
Figure 1.7 の青い曲線は、入力波形のデューティーサイクル50%、繰り返し周波数の範囲25 kHz~750 kHzで測定した出力パルスに対して計算した品質係数です。繰り返し周波数が83.3 kHzのときの品質係数は0.87で、品質係数の最大値1に近い値です。83.3 kHzの場合に得られる高い品質係数は、3 dBカットオフ周波数と入力される方形パルス列の繰り返し周波数との比に対して最小推奨値を提言している9倍ルールを裏付けるものです。
繰り返し周波数250 kHz、デューティーサイクル50%の場合に得られる品質係数0.58は、出力信号のパルス形状に歪みが見られたものの、正弦波よりは方形波に近いという定性的な観察結果と符合します。このケースでは、入力された信号成分の中で750 kHzのシステム帯域幅内の周波数成分は2つしかありません。繰り返し周波数が750 kHzになると出力波形は正弦波になり、品質係数はゼロになります。
デューティーサイクルが20%のときの品質係数は赤の曲線で表されています。繰り返し周波数が83.3 kHzのときの品質係数0.68は、方形として識別可能なパルス形状に対応します。しかし、繰り返し周波数が83.3 kHzでデューティーサイクルが50%のとき(品質係数0.87)に比べてパルスの歪みは大きくなっています。これは、繰り返し周波数を維持しながらデューティーサイクルを減少させると、出力パルスの歪みが大きくなることを示しています。デューティーサイクル20%のときに0.87の品質係数を得るには、繰り返し周波数を約33 kHzまで下げる必要があります。
デューティーサイクル20%の波形の繰り返し周波数を約250 kHzに上げた場合、品質係数はゼロとなります。より高い繰り返し周波数になると、品質係数はマイナスの値になります。物理的には、これは立ち上がり時間が入力パルスの幅よりも長いことを意味します。この状況で立ち上がり時間を正確に測定することは容易ではありません。
緑色の曲線(80% High)は入力信号のデューティーサイクルが>50%の場合の品質係数を表しており、その最小値は正の値です。曲線がゼロに到達しないため、これらの品質係数をほかのデューティーサイクルのケースと比較することは困難です。さらに、品質係数はパルスの形状を評価しますが、より歪みが現れる出力波形のローレベルについては評価していません。そのような懸念に対して、品質係数をローレベルの幅を用いて計算することもできます。デューティーサイクル80%のデータのローレベルの幅から計算された曲線(金色)は、予想通りデューティーサイクル20%のデータに類似しています。
Figure 1.7 にプロットされた品質係数は、パルス幅、繰り返し周波数、および入力信号のデューティーサイクルが出力パルスの歪みに対して与える影響を簡潔に示しています。他のパラメータが一定のとき、下記のような場合には出力信号の歪みは増加します。
- 繰り返し周波数が増加したとき
- デューティーサイクルが減少したとき
- システムの帯域幅が減少したとき
9
追加情報
こちらの実験で使用された当社製品および関連製品については下記のリンクからご覧ください。
- ピグテール付き半導体レーザ用マウント付き電流/温度コントローラCLD1010LP
- 980 nmピグテール付き半導体レーザ
- 可変光ファイバ減衰器VOA980-FC
- 1 GHz FC/PCファイバ入力フォトディテクタDET02AFC
その他の技術情報をご覧になりたい方は
こちらをクリックしてください。
10
| Posted Comments: | |
| No Comments Posted |
 Products Home
Products Home

 パルスの歪み
パルスの歪み