ローパスシステムにおける立ち上がり時間と帯域幅の関係

Please Wait
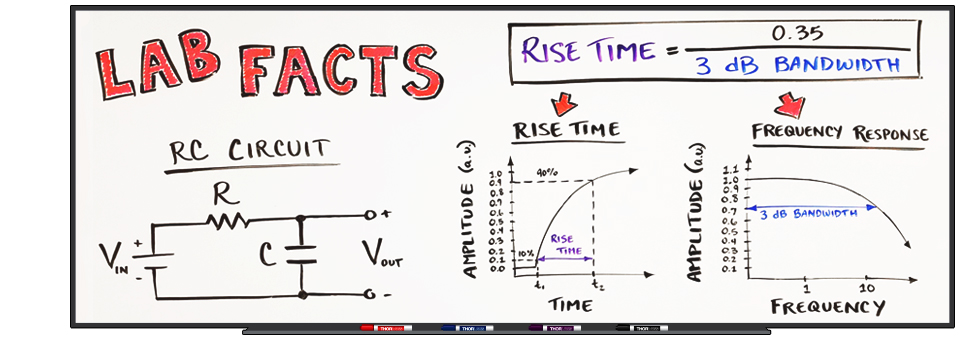
立ち上がり時間と3 dB帯域幅は密接に関係しており、どちらも入力信号の急激な変化に対してシステムが応答可能な限界を表すパラメータです。立ち上がり時間と3 dB帯域幅は反比例し、システムがRCローパスフィルタに似た応答を示す時の比例定数は約0.35です。この2つのパラメータ間の関係式は大変有用で、片方しか分からない場合でも、これによりもう一方を求めることができます。システムの機能とアプリケーションの要件に応じて、片方、あるいは両方のパラメータを参照することが便利な場合があります。
立ち上がり時間は時間で測定されますが、3 dB帯域幅は電気的な周波数で測定されます。立ち上がり時間は、ステップ関数の入力に対する応答出力信号の立ち上がりエッジ上の2つの点の間の時間です。3 dB帯域幅は、システムの周波数応答から求められます。立ち上がり時間と3 dB帯域幅の反比例の関係は、抵抗器とコンデンサの直列接続による理想的なRCローパスフィルタの時間応答および周波数応答から導くことができます。
この実験データでは、RCローパスフィルタのモデルを使用して下記の関係式を導きます。
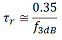
ここで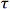 r は出力信号の立ち上がりエッジの10%から90%までの立ち上がり時間、f3dBは3 dB帯域幅です。この関係式は、多くのフォトダイオードを用いたシステムのほか、1次遅れ系の電気システムや電気光学システムにおいて有効です。また、この実験データではフォトダイオードを用いたシステムにおける立ち上がり時間または3 dB帯域幅を測定し、この2つのパラメータの関係式を使用して測定しなかったパラメータを求める例もご紹介しています。
r は出力信号の立ち上がりエッジの10%から90%までの立ち上がり時間、f3dBは3 dB帯域幅です。この関係式は、多くのフォトダイオードを用いたシステムのほか、1次遅れ系の電気システムや電気光学システムにおいて有効です。また、この実験データではフォトダイオードを用いたシステムにおける立ち上がり時間または3 dB帯域幅を測定し、この2つのパラメータの関係式を使用して測定しなかったパラメータを求める例もご紹介しています。
立ち上がり時間とは?
Click to Enlarge
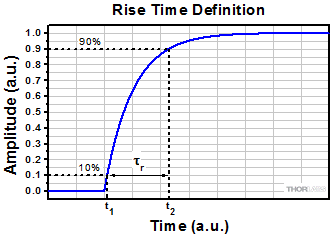
図 1:立ち上がり時間は、曲線の立ち上がりエッジ上にある2つの点の間の時間です。一般に曲線上の10%および90%の点が使用されますが、ほかの点が選択される場合もあります。
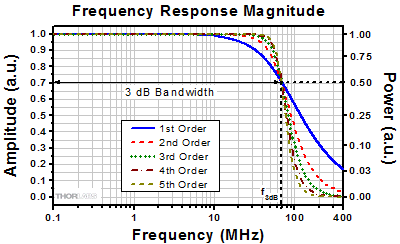
立ち上がり時間(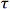 r)は、信号の立ち上がりエッジ上にある2つの点の間の時間です。一般に曲線上の10%および90%の点が使用されますが、曲線上のほかの点が選択される場合もあります。システムの立ち上がり時間が明記されている場合、それは入力信号の変動に対するシステムの最速応答時間を示しています。入力信号にシステムの応答速度よりも速い変動信号が含まれている場合、それに対応する出力信号は入力信号よりも滑らかで幅の広い信号になります。
r)は、信号の立ち上がりエッジ上にある2つの点の間の時間です。一般に曲線上の10%および90%の点が使用されますが、曲線上のほかの点が選択される場合もあります。システムの立ち上がり時間が明記されている場合、それは入力信号の変動に対するシステムの最速応答時間を示しています。入力信号にシステムの応答速度よりも速い変動信号が含まれている場合、それに対応する出力信号は入力信号よりも滑らかで幅の広い信号になります。
システムの立ち上がり時間の測定方法は?
システムの最小立ち上がり時間は、ある安定した信号(ローレベル)から、より高い位置の安定した信号(ハイレベル)に急激に変化する信号を入力信号として用いることで求めることができます。ローレベルからハイレベルへのジャンプは、システムの応答速度よりも速い必要があります。このタイプの信号はステップ関数と呼ばれています。図1のように、これによって得られた出力信号の立ち上がりエッジを用いて、システムの立ち上がり時間を測定します。
1
システムの3 dB帯域幅とは?
Click to Enlarge
図 2:ローパスフィルタEF124の3 dB帯域幅を0 Hz~64.5 kHzで測定。電圧信号あるいは電流信号のスケール因子0.707は、パワーのスケール因子(0.707)2 = 0.5に相当します。
3 dB帯域幅は、システムが応答できる電気的な周波数範囲を示す量です。入力信号の3 dB帯域内の周波数成分はシステムで若干減衰しますが、その帯域外では大きく減衰します。システムの周波数応答を表すデータとしては、入力信号と出力信号間のスケール因子の周波数依存性が示されます。
例として、図2に電圧信号を入力とするローパスフィルタの周波数応答データを示します。電圧信号や電流信号は、振幅という観点からも、あるいはパワーという観点からも見ることができます。信号のパワーは電圧あるいは電流の二乗に比例するため、パワーのスケール因子は振幅のスケール因子の二乗と等しくなります。
3 dB帯域幅は、振幅のスケール因子が≥0.707の周波数範囲を指します。これはパワーのスケール因子が≥0.5の範囲と等しくなります。パワー比≥0.5をデシベルで表すと≥-3 dBに相当します。「3 dB帯域幅」ではマイナス記号は省略されています。
システムの3 dB帯域幅内の入力信号成分は、出力信号において支配的になります。システムの3 dB帯域幅が入力信号の周波数範囲と完全にオーバーラップしたとき、出力信号は入力信号をよく表すことができます。
3 dB帯域幅の測定方法は?
システムの帯域幅は、一連の正弦波信号を入力することで測定できます。正弦波はすべて同じピーク-ピークの振幅を有する必要がありますが、その周波数は測定したい周波数範囲内の様々な周波数に固定して測定する必要があります。最も低い周波数としては 0 Hzに近い値をとるのが一般的です。異なる周波数の正弦波信号を入力するたびに、出力信号のピーク-ピーク振幅を測定します。このピーク-ピークの測定値をある基準値で割ることにより、規格化された振幅スケール因子が得られます。この基準値としては、しばしば最も低い周波数の入力信号のピーク-ピーク値が用いられます。
2
RCローパスフィルタの周波数応答をモデルにできるケースとは?
Click to Enlarge
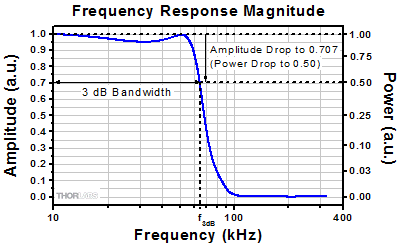
図 3:システムの影響により、一般に各周波数成分の入力信号と出力信号の振幅と位相には差異が生じます。
Click to Enlarge
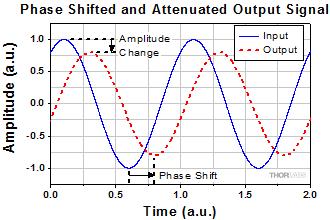
図 4:RCローパスフィルタ回路は1次のローパスフィルタで、周波数が10倍大きくなると振幅は1/10に減少します。より高次のフィルタでは、カットオフ周波数付近での曲線の傾斜がより急峻になります。
システムの周波数応答は、入力信号の各周波数成分の振幅と位相に対するシステムの影響を表しています。しばしば入力信号の成分は様々な周波数で振動する正弦波曲線で表され、これはフーリエ級数やフーリエ変換による表現と一致します。図3は正弦波信号成分の典型的な入力信号と出力信号で、位相や振幅に差異が生じることを示しています。入力信号の各周波数成分の振幅に対するシステムの影響は、上記の2ページ目で説明したようにシステムの振幅周波数応答によって表されます。
ローパスフィルタと同様の振幅周波数応答を有するシステムでは、振幅スケール因子は高周波側よりも低周波側で非常に大きくなるような周波数依存性をもちます。このような応答により、システムはカットオフ周波数(f3dB )よりも高周波側の周波数の成分を大きく減衰させます。システムの出力信号では、入力信号の低周波数成分がより支配的になります。
ローパスフィルタの種類は次数によって表されますが、それはカットオフ周波数近辺における振幅周波数応答曲線の傾斜によって求められます。応答曲線の傾斜がおおよそω-Nの割合で減少するとき、フィルタはN次のローパスフィルタとなります。図4には理想的な1次~5次のローパスフィルタの曲線が描かれており、各スロープはそれぞれω-1~ω-5に比例して小さくなっています。 図2のような応答を示すローパスフィルタは5次のローパスフィルタです。
RCローパスフィルタは1次のローパスフィルタであるため、周波数10ωにおける周波数応答の振幅は周波数ωにおける振幅の約1/10です。この実験データでは、振幅周波数応答が1次のRCローパスフィルタに近いシステムに適した関係式を提供します。システムの応答がこれに近いときは、RCローパスフィルタ回路のモデルでそのシステムの応答についての妥当な概算値を得ることができます。この後では、RCローパスフィルタに関する詳細な情報と、システムの応答がこの種のフィルタに近いかどうかを決定するためのアプローチについて提示しています。
なお、周波数応答の測定では、セットアップの機器およびデバイスだけでなく、ケーブルの電気特性や読み取り機器の応答特性の影響も受けることに留意しなければなりません。
3
ローパスフィルタに適したモデルとは?
Click to Enlarge
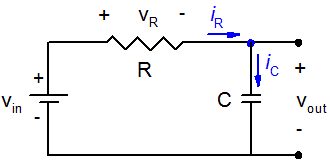
図 5:RCローパルフィルタ回路は、ローパスフィルタの性質を表すシンプルなモデルとしてよく使用されます。立ち上がり時間と3 dB帯域幅の関係を導出するのにも使用できます。
図5に示すRCローパスフィルタ回路は、ローパスフィルタの動作を表すモデルとしてよく使用されます。ON/OFF切り替え可能な電圧源から、電圧信号(vin )が入力されます。コンデンサ(C )の両端子間で、出力電圧信号(vout )を測定します。この端子間の抵抗は無限大であるため、電流は抵抗器(R )、コンデンサ、および電圧源を含むループにのみ流れます。その結果、回路に流れる電流(i )は、次のように抵抗器およびコンデンサに流れる電流に等しくなります。
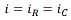 .
. ここで、iRおよびiC はそれぞれ抵抗器およびコンデンサに流れる電流です。抵抗器の両端間の電圧(vR )はオームの法則によって
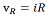 ,
, と与えられ、電流に比例します。この回路のローパス特性は、入力電圧のスイッチが長時間オフになっていた後に突然ONになって一定の電圧が維持されたとき、回路の電圧と電流がどのように変化するかを考えることでモデル化することができます。電圧源のスイッチをONにする前には回路に電流は流れていないため、コンデンサに電荷は無く、コンデンサおよび抵抗器のそれぞれの両端間の電圧は共にゼロです。電圧源のスイッチをONにすると、回路に電流が流れ始めますが、その大きさはコンデンサによって制限されます。電流は
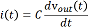 ,
, で与えられ、コンデンサの両端間の電圧(vout ) を時間(t )で微分した量に比例して流れます。電流は、voutが時間変化するときにのみ流れます。回路内の電圧の関係式
 ,
,およびオームの法則により、電流が流れなくなるとvRは0まで下がり、voutと is equal to vin は等しくなります。電圧源がONになった時から電流が止まるまでの間における、電流と電圧の動的な変化からモデルが導出されます。
4
パルスの立ち上がり時間の時間依存性を表す式は?

Click to Enlarge
図 6:RCローパス回路に定電圧が突然入力された時の出力電圧信号の立ち上がりエッジ
Click to Enlarge
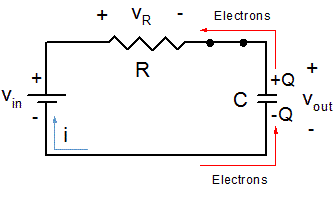
図7: 電子はコンデンサの底部プレートに蓄積し、上部プレートからは流れ出します。負の電荷(-Q)と正の電荷(+Q)が増えることにより、時間の経過とともにvoutが増加します。抵抗(R )と電気容量(C )の値は一定です。
図6の時間に依存する立ち上がりエッジの信号は、図7のRCローパス回路を用いてモデル化できます。電圧源をONにすることは、供給電圧が0 Vから一定の電圧値vin に突然ジャンプすることに対応します。電圧が突然供給されることにより、電流が回路内に流れ始めます。
電子は電圧源の負端子からコンデンサの底部プレートに流れます。電子はまたコンデンサの上部プレートから電圧源の正端子へと流れます。荷電粒子はコンデンサを通過して流れることができないため、電子の流入に応じて電子はコンデンサの底部プレートに蓄積し、コンデンサの上部プレートでは電子の空孔数が増加します。
負の電荷(-Q )がコンデンサの底部プレートに蓄積し、同じ量の正の電荷(+Q )が上部プレートに蓄積します。この分離した正と負の電荷によりコンデンサの両端に電圧voutが発生し、その大きさはコンデンサの1つのプレート上の全電荷量(Q )に比例します。この電圧は電流が流れ続ける限り増加します。*
プレートに電荷が蓄積される速度が最も早いのは電圧源が最初にONになったときで、同時にvoutも最速で増加します。荷電粒子の流入はvout によって阻止されるようになってきます。この対抗する電圧が大きくなれば、コンデンサのプレートに電荷を蓄積する速度は遅くなります。voutとvinnが等しくなると、電流は流れなくなります。
ステップ関数の電圧入力に対するvoutの応答に関する説明は、図6のグラフとも整合します。このような応答は数式では
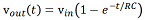 ,
,と表され、この式はフルレポートの中で上記の4ページ目のカードの式を用いて導出されています。
*電流は電子の流れとは反対の方向に流れると定義されています。電流の方向は図7では青い矢印で示されています。
5
振幅スケール因子の周波数依存性を表す式は?

Click to Enlarge
図 8:RCローパスフィルタ回路は、ローパスフィルタの動作についてのシンプルなモデルとしてよく使用されます。立ち上がり時間と3 dB帯域幅の関係を導出するのにも使用できます。
図8の回路と4ページ目のカードに示した式を用いて、周波数応答を表す式を導くことができます。周波数応答は入力信号と出力信号の関係を記述しますが、その関係はシステムによって決定されます。従ってこの方法では、周波数に依存するvoutとvinの比は、すべてシステムのコンポーネントの関数として記述される必要があります。
このアプローチはフルレポートその詳細が記載されています。それによると周波数応答(H )は複素数で表され、各入力信号成分の位相と振幅に対するシステムの影響を記述しています。周波数応答の振幅成分は周波数応答の絶対値(|H | )で与えられ、振幅のスケール因子を表します。
これにより、RCローパスフィルタに入力された各周波数成分の振幅のスケール因子は
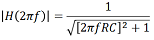
で表され、入力信号の周波数(f )、抵抗(R )、および電気容量(C )にのみ依存することが分かります。パワーのスケール因子(|H |2 )は、次のように振幅のスケール因子を二乗して求められます。
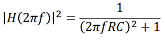 .
.6
立ち上がり時間と3 dB帯域幅を関連付ける最後のステップは?

Click to Enlarge
図 9:立ち上がり時間は、曲線の立ち上がりエッジ上にある2つの点の間の時間です。一般に曲線上の10%および90%の点が使用されますが、ほかの点が選択される場合もあります。
まず立ち上がり時間を表す式を求めます。
パルスの立ち上がりエッジの時間依存性を表す式は
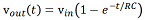 ,
,で与えられ、これを用いて立ち上がり時間とRC積の関係を求めます。図9を参照し、t1での信号レベルが 0.1、t2での信号レベルが 0.9、そして無限時間後での信号レベルが1であることから、この関係を見出すことができます。これらの信号レベルの値と立ち上がり時間の定義(t2 - t1 )を用いて、次の式を得ることができます。
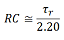 ,
, この式には立ち上がり時間とRC積のみが含まれています。
次に、3 dB帯域幅の式を求めます。
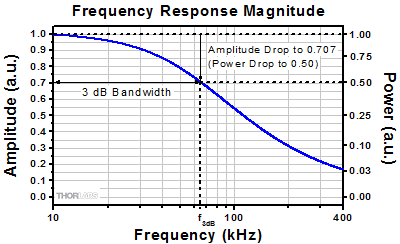
パワーについてのスケール因子の周波数依存性を表す式
Click to Enlarge
図10:1次のローパスフィルタであるRCローパスフィルタの3 dB帯域幅。振幅のスケール因子0.707は、パワーのスケール因子(0.707)2 = 0.5に相当。
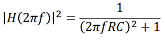 ,
,を使用して、3 dB帯域幅(f3dB )とRC積の関係を求めます。図10に示すように、3 dB帯域幅の高周波側の境界では、パワーのスケール因子は最大値の半分になります。式の左辺を0.5とすると次の式
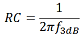 ,
, が得られ、これは3 dB帯域幅とRC積の関係を表しています。
最後に、両方の式を組みあわせてRCの定数を消去します。
上の2つステップでそれぞれ得られたRCを表す式を組み合わせることで、立ち上がり時間と3 dB帯域幅の関係を表す式が得られます。次の式
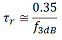 ,
, は大変便利で、3 dB帯域幅が既知のときには立ち上がり時間を計算することができ、またその逆の計算にも使えます。
この関係式はローパスフィルタのモデルを用いて求めているため、システムがローパスフィルタのように振舞う場合にのみご使用ください。理想的なRCローパスフィルタ回路で、現実のシステムの動作を完全にモデル化するのは困難です。従って、この式は実際のシステムのパラメータを推定するのには便利ですが、正確な結果を与えることを期待するものではありません。正確な値が必要な場合は、パラメータを直接測定してください。両方のパラメータが必要な状況で、どちらか一方のみしか測定できない場合には、他方はフーリエ変換に基づく厳密な方法で計算することができます。
7
立ち上がり時間から3 dB帯域幅を推定する例
フォトダイオードを用いたシステムではしばしば負荷抵抗器が用いられ、それによりフォトダイオードからの電流信号をより測定が容易な電圧信号に変換します。負荷抵抗としてどのような値を選ぶかによって、立ち上がり時間や3 dB帯域幅を含む様々なシステム性能が変化します。ここではフォトダイオードを用いたシステムの立ち上がり時間を測定しましたが、各測定では負荷抵抗の値を変えました。図11と12に、立ち上がり時間の2つの測定例を示します。この作業では、システムの3 dB帯域幅の値を求めることも目的としています。このシステムからの出力信号の立ち上がりエッジとRCローパス回路の立ち上がりエッジが同様であれば、下記の式
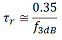 ,
,から3 dB帯域幅の妥当な推定値が得られます。RCローパス回路の出力信号の立ち上がりエッジの式
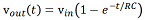 ,
,を用いると、図11と12の赤い曲線が得られました。これらの曲線はデータに良くフィットしているため、このカードの上部の式を用いて、それぞれの負荷抵抗におけるシステムの3 dB帯域幅を推定しました。測定された立ち上がり時間と3 dB帯域幅の推定値を表1に示します。
この2つのパラメータは逆数の関係にあり、システムの立ち上がり時間が長くなるとシステムの帯域幅は減少します。入力信号の周波数がシステムの帯域幅を超えたときは、システムによりそのような高い周波数の信号は減衰します。その結果、出力信号は入力信号に比べてより丸みを帯びた幅の広い信号になります。その様子は図11と12で見ることができます。立ち上がりエッジは垂直であるのが理想ですが、立ち上がり時間が長くなる(そして帯域幅が減少する)につれて傾斜は緩くなっています。
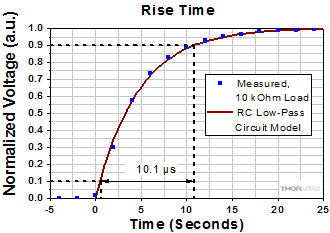
Click to Enlarge
図11:有効負荷抵抗が10 kΩのフォトダイオードシステムで測定された立ち上がり時間は10.1 µsでした。RCローパスフィルタモデルを用いて計算された立ち上がりエッジ(赤い曲線)はデータにフィットしています。
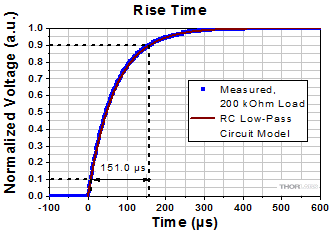
Click to Enlarge
図12:有効負荷抵抗が200 kΩのフォトダイオードシステムで測定された立ち上がり時間は151.0 µsでした。RCローパスフィルタモデルを用いて計算された立ち上がりエッジ(赤い曲線)はデータにフィットしています。
表1: 図11と12に示す立ち上がり時間の測定値から推定された3 dB帯域幅
| 3 dB帯域幅から立ち上がり時間を推定する例 | ||
|---|---|---|
| Effective Load Resistance | Measured Rise Time | Calculated 3 dB Bandwidth |
| 10 kΩ | 10.1 µs | 34.7 kHz |
| 200 kΩ | 151.0 µs | 2.3 kHz |
8
3 dB帯域幅から立ち上がり時間を推定する例
フォトダイオードを用いたシステムの性能は、フォトダイオードに加える逆バイアス電圧にも影響されます。システム応答への逆バイアス電圧の影響は、先ほどの例で用いたシステムよりも応答の早いシステムで調べました。このケースでは立ち上がり時間がナノ秒程度になるため、その測定は難しくなります。そのため、直接立ち上がり時間を測定するのではなく、システムの周波数応答を測定し、そのデータから下記の式を用いて推定しました。
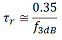 .
.測定結果を図13と14に示しますが、対応するRCローパスフィルタの応答モデルとしては下記の式
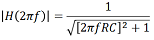
を適用し、その結果をそれぞれの図に赤い曲線で示しました。モデルの応答と測定された応答は良くフィットしているため、このカード上部の式を用いることで、様々な逆バイアス電圧に対するシステムの立ち上がり時間を適切に推定できると期待できます。表2に測定された3 dB帯域幅とそれから推定された立ち上がり時間を示します。
これらの測定から、フォトダイオードの逆バイアス電圧を増加させることは、システムの3 dB帯域幅を増加させるのに効果的であることが分かります。3 dB帯域幅が増加すると、立ち上がり時間は短くなります。これにより入力信号の突然の変化に対するシステムの応答速度が速くなり、入力信号の鋭くかつ速い変化もシステムの出力信号で再現できるようになります。しかし、過度に高い逆バイアス電圧をかけるとフォトダイオードがダメージを受けるため、このアプローチで得られる帯域幅の増加には限界があります。
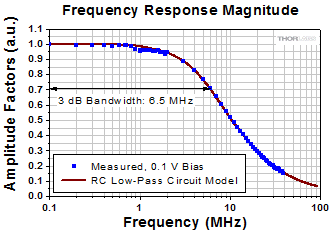
Click to Enlarge
図 13:フォトダイオードの逆バイアス電圧が0.1 Vのときに測定されたシステムの3 dB帯域幅は6.5 MHzでした。RCローパスフィルタのモデルを用いて計算された周波数応答(赤い曲線)はデータにフィットしています。
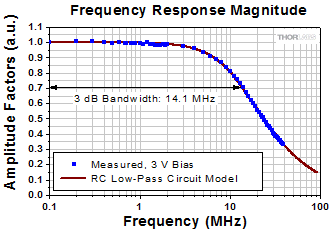
Click to Enlarge
図14:フォトダイオードの逆バイアス電圧が3 Vのときに測定されたシステムの3 dB帯域幅は14.1 MHzでした。RCローパスフィルタのモデルを用いて計算された周波数応答(赤い曲線)はデータにフィットしています。
表2: 図13と14に示す3 dB帯域幅の測定値から推定された立ち上がり時間
| Rise Time Estimated from 3 dB Bandwidth | ||
|---|---|---|
| Bias Voltage | Measured 3 dB Bandwidth | Calculated Rise Time |
| 0.1 V | 6.5 MHz | 54.1 ns |
| 3.0 V | 14.1 MHz | 24.7 ns |
9
追加情報
この実験に関連した製品一覧
- ピグテール付き半導体レーザ用マウント付き電流/温度コントローラCLD1010LP
- 980 nmピグテール付き半導体レーザ
- 可変光ファイバ減衰器VOA980-FC
- • 1 GHz FC/PCファイバ入力フォトディテクタDET02AFC
システムの立ち上がり時間と3 dB帯域幅が、矩形波あるいは方形パルストレインの歪みにどのように影響するかについては、
実験データのページをご覧になるか、こちらをクリックして詳細レポートをダウンロードしてください。
その他の技術情報をご覧になりたい方は
こちらをクリックしてください。
10
| Posted Comments: | |
| No Comments Posted |
 Products Home
Products Home

 立ち上がり時間と3 dB帯域幅
立ち上がり時間と3 dB帯域幅